| Titel: | Ueber das Fehlerglied der einfachen Schiebersteuerung; von Victor H. Sirk in Pola. |
| Autor: | Victor H. Sirk |
| Fundstelle: | Band 220, Jahrgang 1876, Nr. , S. [ad] |
| Download: | XML |
Ueber das Fehlerglied der
einfachen Schiebersteuerung; von Victor H. Sirk in Pola.
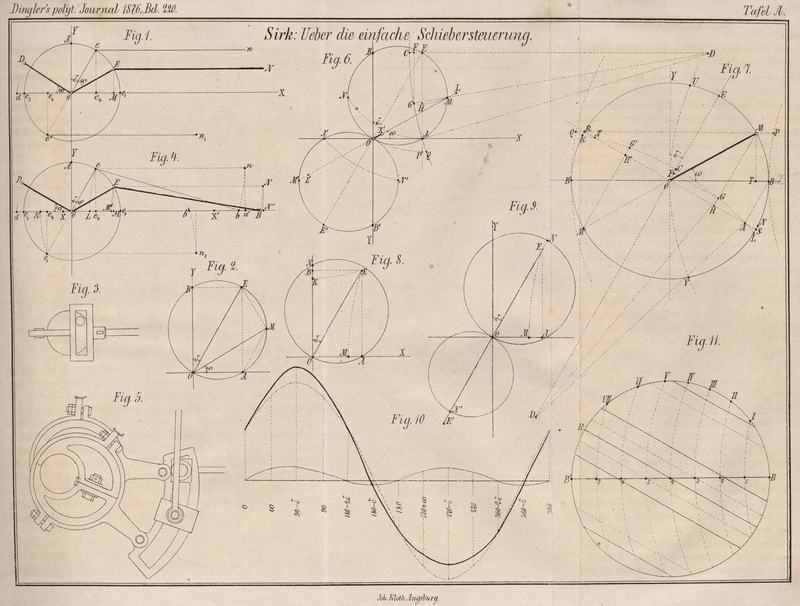
Mit Abbildungen auf Taf. A.
Sirk, über das Fehlerglied der einfachen
Schiebersteuerung.
Die Dampfvertheilung, d. i. das
abwechselnde Zulassen des Arbeitsdampfes zu den beiden
Cylinderenden und dessen Entleerung, wird bei stationären
Maschinen und insbesondere bei Dampfmaschinen, welche der
Transportindustrie dienen, fast ausnahmslos durch
Schiebersteuerungen besorgt, die durch Kurbeln oder Excenter
bewegt werden. Der Muschelschieber der einfachen
Schiebersteuerung überdeckt in der mittlern Stellung die beiden
Einströmungsspalten — um die äußere Deckung auf der
Admissionsseite und um die innere Deckung auf der Exhaustseite.
Es genügt demnach, den Schieberweg,
d. i. jene Strecke, um welche die Schieberplatte aus der
mittlern Stellung gerückt wurde, festzustellen, um die jeweilige
Eröffnung des Canals zu bestimmen, die einem gegebenen
Drehwinkel der Kurbel entspricht. Man gewinnt ein Bild der
Dampfvertheilung, indem man den Schieberweg vom Drehwinkel
ω abhängig durch die festen Dimensionen der Steuerung
ausdrückt. Das Bewegungsgesetz der Schieberplatte ist durch die
Excentricität, die Länge der Excenterstange und relativ zur
Kurbelbewegung durch den Voreilungswinkel bedingt.
Es bedeutet Od in Figur 1
die Kolbenkurbel und Oe die
Schieberkurbel oder Excentricität; eOA = δ ist der Voreilungswinkel. Denkt man sich
vorerst die Bewegung des Kreisexcenters durch eine unendlich
lange Excenterstange e n auf den
Schieber übertragen, so folgt jeder ihrer Punkte dem gleichen
Bewegungsgesetze, weshalb ein beliebiger Punkt der Schubstange
e n — beispielsweise auch der
Mittelpunkt e der excentrischen
Scheibe — als Schiebermittel angesehen werden kann. Der
Voraussetzung einer unendlich langen Excenterstange könnte
constructiv durch Figur 3
Genüge geleistet werden, indem die Schieberkurbel in einem
Gleitrahmen der gerade geführten Schieberstange arbeitet.
Bei der Drehung der Achse wird der Mittelpunkt e den Kreis der Excentricität
beschreiben und das Schiebermittel zwischen den Punkten e1, und
e2
führen, der Durchmesser e1 e2 stellt den vollen Ausschub dar.
Für die beim Drehwinkel dOD = eOE = ω stattfindende allgemeine
Lage der Kolbenkurbel in DO befindet
sich das Schiebermittel in E
— oder mit Bezug auf die Strecke e1 e2 in M, weil die unmittelbar auf den Schieber
übertragene Horizontalbewegung des Punktes E durch dessen Projection M dargestellt wird. Der Schieber muß auf
gleiches Voreilen adjustirt werden, weshalb bei den Stellungen
der Kolbenkurbel in den todten Punkten gleiche Ausschübe
stattfinden sollen. Der Schwingungsmittelpunkt der
Schieberbewegung ist daher zwischen den beiden Stellungen e3 und
e4,
welche der Schieber hierbei einnimmt, zu suchen.
Nach der Construction der Figur muß Oe3 = Oe4
sein, weshalb für diesen Fall der Schwingungsmittelpunkt mit dem
Punkte O zusammenfällt. Für die
allgemeine Lage ist daher OM der
Schieberweg, welcher sich aus dem Dreiecke OEM mit OM =
s = r
sin
(ω + δ) bestimmt (Zeuner: Schiebersteuerungen S. 22). Denkt man sich nun das
rechtwinklige Dreieck OEM aus der
Figur 1 herausgehoben und in Figur 2 an
die Linie OE = r, welche unter dem Voreilungswinkel YOE = δ gezogen wurde, so muß der
Punkt M in der Peripherie eines
Kreises liegen, welcher über OE als
Durchmesser verzeichnet wurde, weil alle Winkel im Halbkreise
rechte Winkel sind. Nachdem aus Figur 1
< EOM = 90 - (ω +
δ) ist, folgt, daß < MOA = ω sein muß, und es stellt daher die Sehne MO den Schieberweg für den Drehwinkel
ω unmittelbar dar.
Nimmt man OM als die allgemeine Lage
der unter dem Drehwinkel MOA =
ω gezogenen Sehne an und vervollständigt die Figur durch
die Linien AM und AE, so folgt, weil in einem
Sehnenvierecke AOEM das Product der
Diagonalen gleich der Summe der Producte aus den Gegenseiten
ist:
OM × AE = AM
× OE + OA × EM.
Durch Einsetzen der Werthe AE = r cos
δ, AM = r sin
ω (als Sehne des Peripherieminkels ω), OE = r, OA = r sin
δ, EM = r cos (ω + δ) erhält
man aus obiger Gleichung:
OM × r cos δ = r sin
ω × r + r sin δ × r cos (ω + δ), woraus
sich OM = r sin (ω + δ) berechnet.
Es stellt demnach die unter dem Drehwinkel ω gezogene
Sehne den jeweiligen Schieberweg nach der angenommenen
Bewegungsübertragung dar. (Zum gleichen Resultate gelangt man
durch Betrachtung des Sehnenviereckes OBEM. Der einfachste Beweis für die Construction der
Function r sin (ω + δ) von
Haedicke findet sich in diesem
Journal, 1870 197 99.)
Es ist ersichtlich, daß das Zeuner'sche Kreisdiagramm dem Einfluß
der endlichen Länge der Excenterstange nicht Rechnung trägt und
die Normaldampfvertheilung nach den Daten r und δ so angibt, als ob das Excenter an einer
unendlich langen Schubstange oder in einem Gleitrahmen arbeiten
würde. Bei besonderer Betrachtung der Locomotivsteuerungen
erfordert dieser beirrende Einfluß keine Berücksichtigung, wohl
aber bei Schiffsmaschinen, bei welchen häufig die Excenterstange
durch Raumverhältnisse außerordentlich kurz bedingt wird.
Beispielsweise ist in Figur 5
die äußere Steuerung einer ausgeführten Schiffsmaschine
dargestellt, die 2r = 145 und 1 =
355 aufweist — Daten, welche das Verhältniß l/r <
5 ergeben, obwohl dieses nach den angegebenen, nicht
übereinstimmenden Coten 5¼ sein soll. Durch die
vorgeführte Anordnung werden übrigens nicht die ungünstigsten
Verhältnisse dargestellt, welche noch Verwendung finden. Dem
Uebelstande wird zuweilen durch die Anbringung von Schiebern mit
doppelter Einströmung begegnet, weil die Canalbreite und der
Schieberweg vermindert wird. Die Erzeugung und Adjustirung der
Vertheilungsschieber wird aber hierbei umständlicher und
kostspieliger, weshalb in vielen Fällen zum Nachtheil der
richtigen Dampfvertheilung der einfache Schieber selbst für
minder günstige Verhältnisse beibehalten wird.
Die Abweichung der wirklichen Schiebercurve von dem
Kreisdiagramme der Normaldampfvertheilung wird von Zeuner in seinem bekannten Werk über
Schiebersteuerungen (auf dessen vierte Auflage alle bezogenen
Seitenzahlen hinweisen) durch das Fehlerglied z in mathematischer Form dargestellt und
in seinem ersten Ausdrucke durch Herm. Fuhst graphisch verzeichnet (vgl. * 1858 150 241).
Das Rechnen der Werthe für den Schieberweg hat für den
Constructeur wenig Anziehendes — eine auf unmittelbare
graphische Versuche basirte Construction von Schieberellipsen
ist ermüdend und im verkleinerten Maßstab von problematischem
Werth, so daß der Constructeur gezwungen ist, zu
Steuerungsmodellen seine Zuflucht zu nehmen, wenn eine
Vernachlässigung des Einflusses der endlichen Länge der
Excenterstange zu beirrenden Differenzen Anlaß gibt.
Steuerungsmodelle aber, welche häufig in sehr verjüngtem
Maßstabe ausgeführt werden, bieten bei dem todten Gang und
falschen Spiel der einzelnen Gelenke geringe Sicherheit für das
Gelingen des richtigen Entwurfes einer Steuerung und erfordern
große Genauigkeit der Beobachtung, weil die Momente und Phasen
der Dampfvertheilung nicht unmittelbar präcis markirt werden,
wie auch Ausdauer im Ausführen von Versuchsreihen, welche es
erklärlich scheinen läßt, daß Schiffsmaschinen in ihren
Diagrammsätzen häufig so mangelhafte Dampfvertheilung beim
Wechseln des Füllungsgrades anzeigen. Die Aufgabe, eine für
Füllungen von 10 bis 50 Proc. vollkommen richtig functionirende
Steuerung zu erlangen, ist bei der complexen Wirkungsweise der
gebräuchlichsten Dampfvertheilungsapparate bei Schiffsmaschinen
von der größten Wichtigkeit und Schwierigkeit, und erschöpft an
Steuerungsmodellen die Geduld selbst gewissenhafter
Constructeure.
Die unmittelbare Folge einer mangelhaften Dampfvertheilung ist
ein unruhiger hinkender Gang der Maschinen, welcher sich bei
Aenderungen des Füllungsgrades so vermehren kann und vermehrt,
daß ein Ausnützen der Maschinen nach ihrer
Maximalleistungsfähigkeit mit der nöthigen Sicherheit des
Betriebes unvereinbar ist. Verbinden sich diese Folgen an einer
mit schlechtem Materiale gebauten Maschine mit einem wenig
rationellen Betrieb, so sind Stöße und Schläge, gelockerte
Dichtungen, warmlaufende Lager und angegriffene Drehzapfen
— kurz häufige Havarien und rasche Abnützung die
Consequenzen eines viereckigen stoßenden Ganges der Maschinen
und theilweise die mittelbaren Folgen einer unrichtigen
Dampfvertheilung.
Zur Versinnlichung der Dampfvertheilung bei Schiffsmaschinen mit
kurzen Excenterstangen und zur Lösung aller einschlägigen Fragen
eignen sich besonders das Zeuner'sche und Reuleaux'sche
Schieberdiagramm, weil der beirrende Einfluß der endlichen Länge
leicht graphisch dargestellt und die Abweichung der wirklichen
Schiebercurve von dem Normalkreisdiagramm durch eine einfache
Construction bestimmt werden kann.
Einfluß der endlichen
Länge der Excenterstange.
Die Führung des Dampfschiebers wird in Wirklichkeit durch eine
Excenterstange besorgt, welche gegen die Führungsmittellinie
eine vom Drehwinkel ω abhängige geneigte Lage einnimmt,
wodurch das Bewegungsgesetz der Schieberplatte beeinflußt und
Abweichungen von der Normaldampfvertheilung hervorgerufen
werden, welche bei geringer Länge der Excenterstangen
berücksichtigt werden müssen.
Es seien in Figur 4
die früher gewählten Bezeichnungen beibehalten und die
Excenterstange in B mit der
Schieberstange in einem Gelenke verbunden. Es mag nun B als Mittelpunkt des Schiebers
angesehen werden, weil alle Punkte der Schieberstange die
gleiche Bewegung verfolgen. Unter der Annahme einer unendlich
langen Schieberstange befände sich der Dampfschieber bei der
allgemeinen Lage DOE in N oder N′. Wegen der geneigten Lage der Excenterstange ist
das Schiebermittel erst in B
angelangt, und es ist daher BN′ die Abweichung gegen den vorigen Fall. Mit
Bezug auf die Strecke e1 e2 befindet sich das Schiebermittel
für den Drehwinkel ω nicht mehr in M, sondern in M′,
welcher Punkt bestimmt wird, indem man aus B den Kreisbogen EM′ verzeichnet. Außerdem muß jedoch berücksichtigt
werden, daß der Schwingungsmittelpunkt bei der erforderlichen
Adjustirung auf ein gleiches lineares Voreilen nach links
verrückt wird. Bei den Stellungen der Dampfkurbel in den todten
Punkten befindet sich der Mittelpunkt der excentrischen Scheibe
in e und e′, der Schieber in b
oder b′, oder auf der Strecke
e1
e2
in L und K. Der Schwingungsmittelpunkt X liegt in der Mitte zwischen K und L, und er erscheint um
OX = Ke3 = Le4 =
bn′ aus dem Mittelpunkt O nach links gerückt. Für den Drehwinkel
ω ist nun XM′ der
Schieberweg, d, i. jene Strecke, um welche der Schieber bei
einer Adjustirung auf gleiches Voreilen aus dem
Schwingungsmittelpunkte X gerückt
ist. Der Schieberweg XM′
stellt sich nun dar als
XM′ =
ξ MO + OX - MM′.
Nun ist aber MO = s der durch das
Kreisdiagramm dargestellte Schieberweg bei unendlich langer
Schubstange, weshalb
ξ = s +
OX - MM′.
Der Ausdruck OX - MM′ stellt also
die durch den Einfluß der endlichen Länge der Excenterstange
hervorgerufene Abweichung von dem durch das Zeuner'sche
Kreisdiagramm angezeigten Schieberweg dar, und es mag dieser
Fehler bei genügender Länge der Excenterstange vernachlässigt
werden oder durch die folgende Construction Berücksichtigung
finden.
Construction des
Fehlergliedes.
Man verzeichnet sich das Zeuner'sche Kreisdiagramm nach der
Normaldampfvertheilung, zieht durch E die Linie ED (Fig.
6) parallel zur OX und
beschreibt aus einem ihrer Punkte D
durch A den Kreisbogen AC mit der Länge der Excenterstange als
Radius. Für die allgemeine Lage der Dampfkurbel unter dem
Drehwinkel ω bestimmt sich das Fehlerglied oder die
Abweichung z = OX - MM′ (Fig. 4),
indem man EH = EM aufträgt und GH parallel zu OX (Fig.
6) zieht.
GH ist das Fehlerglied, und zwar
liegen positive Werthe links und negative Werthe rechts von der
Linie AE. GH als positiver Werth vermehrt den positiven Schieberweg
OM, und man erhält daher den wahren
Ausschlag, indem man ML = GH aufträgt. OL ist der wahre Schieberweg. Für den Drehwinkel 180 +
ω ist der Schieberweg negativ, weil man die Linie OM′ verlängern muß, um die Sehne
OM im positiven Schieberkreis
zu erlangen. Der positive Werth GH
des Fehlergliedes wird den numerisch gleichen Schieberweg OM′ vermindern, und es ist der
wahre Schieberweg OL′ = OM′ - M′L′, wobei M′L′ = GH ist.
Der Beweis für die Richtigkeit der Construction stützt sich auf
eine Vergleichung der Figuren CEA
(Fig. 6) und Le4e (Fig.
4), ferner CFG (Fig.
6) mit MM′E (Fig. 4),
woraus erhellt, daß CE = Le4 =
OX und CF = M′M, weshalb GH = FE = OX - M′M ist. (Es muß noch
erwähnt werden, daß Figur 6
doppelt so große Constructionsdaten aufweist als Figur 4.)
Weiterhin erhellt, daß das Fehlerglied ML (Fig. 6)
nichts anders als der Abstand des Mittelpunktes X′ der Ausschübe für ω und
180 + ω vom Schwingungsmittelpunkt O ist. Für LL′ ist X′ der Mittelpunkt der Schwingung
und OX′ = LM = L′M′.
Für ω = 0 ist das Fehlerglied gleich Null und das
Kreisdiagramm erschöpft in OA die
Function des Schieberweges. Bei der Drehung wird das Fehlerglied
immer größer und vermehrt als positiver Werth den Schieberweg
des Kreisdiagrammes. Bei ω = 90 - δ ist in CE das Maximum der Abweichung erreicht.
(Dieses ist der Abstand des wahren Schwingungsmittelpunktes vom
Mittel des ganzen Ausschubes.) Bei fortgesetzter Drehung wird
die Abweichung der wahren Schiebercurve vom Normaldiagramme
immer geringer, bis sie bei NOA =
180 - 2δ wieder gleich Null wird und die wirkliche
Schiebercurve neuerdings mit dem Normaldiagramme zusammenfällt.
Man erlangt diesen Punkt N, indem
man aus E den Kreisbogen AN verzeichnet. Nachdem < EOA = 90 - δ, folgt < NOA = 180 - 2δ. Das Abschneiden
des Dampfes (Beginn der Expansion) tritt stets in der Nähe
dieses Punktes ein, und man ersieht daher, wie vorzüglich das
Zeuner'sche (als auch das Reuleaux'sche) Diagramm dem Entwurfe
von einfachen Schiebersteuerungen dient, wenn durch die endliche
Länge der Excenterstange nicht bedeutende Aenderungen
hervorgerufen werden.
Von ω = 180 - 2δ bis 180 - δ wächst das
Fehlerglied bis zum Werthe PQ.
Dieses ist nun dem Zeichen nach negativ und vermindert den
positiven Schieberweg. Von 180 - δ bis ω =
180° fällt das Fehlerglied auf Null, nur wird nun der
wirkliche Schieberweg numerisch größer, weil der Schieberweg s und das Fehlerglied z beide negativ sind.
Von ω = 180 bis 270 - δ wächst das Fehlerglied und
vermindert als positiver Werth den negativen Schieberweg. Von
ω = 270 - δ bis 360 - 2δ vermindert sich
z (bis auf den Werth Null) und der
Schieberweg, bis bei 360 - 2δ das Kreisdiagramm wieder
mit der wirklichen Schiebercurve zusammentrifft. Von 360 -
2δ wächst das Fehlerglied numerisch bis
360 - δ und fällt sodann bis ω = 360. In dieser
Periode vermehrt das Fehlerglied den Schieberweg bis 360 -
δ und vermindert denselben von 360 - δ bis auf den
Ausgangspunkt OA.
Gleichung des
Schieberweges.
Mit Bezug auf den geometrischen Zusammenhang der Figur 4
und Beibehaltung der gewählten Bezeichnungen bestimmt sich die
Entfernung des Schiebermittels B für
die allgemeine Lage OE mit OB = OM +
MB. Die entsprechenden Werthe
eingesetzt:
Textabbildung Bd. 220, S. 295
Für die beiden todten Punkte findet
man:
Textabbildung Bd. 220, S. 295
Der Abstand des Schwingungsmittelpunktes
X′ vom Wellencentrum O ist daher gleich:
Textabbildung Bd. 220, S. 295
Der Abstand des Punktes B vom Schwingungsmittelpunkt X′ ergibt den Schieberweg für den
Drehwinkel ω:
BX′ = OB - BX′ = ξ und
Textabbildung Bd. 220, S. 295
Der Schieberweg kann also im Allgemeinen
durch die Sehne des Kreisdiagrammes s = r sin (ω + δ)
dargestellt werden; ξ = s +
z, das Fehlerglied Textabbildung Bd. 220, S. 295
Mit Bezug auf Figur 6
ist
Textabbildung Bd. 220, S. 295
oder da FG =
EM = r
cos
(ω + δ) und AE = r cos δ, so folgt:
Textabbildung Bd. 220, S. 295
woraus ersichtlich ist, daß das
Fehlerglied in Figur 6
auf vollkommen richtige Weise construirt wurde, ferner daß
positive Werthe links von AE
zählen.
Das Fehlerglied in der aufgestellten Form stimmt vollkommen mit
dem von Zeuner (S. 16) entwickelten
Ausdruck überein, wie man sich überzeugt, indem man die
Wurzelgrößen nach dem binomischen Satz in Reihen entwickelt und
mit Hilfe der Formel cos2 α - cos2 β = sin (α + β) ×
sin
(β - α) transformirt; wobei man erhält:
z = r2/2l sin (2δ + ω)
sin
ω + …
Untersuchung des
Fehlergliedes.
Das Fehlerglied Textabbildung Bd. 220, S. 296 wird Null, wenn cos2 (ω + δ) = cos2 δ oder mit Benützung der obigen trigonometrischen
Formel sin (2δ + ω) sin ω = 0 ist. Dieser
Gleichung wird Genüge geleistet durch: ω = 0 und 180 oder
180 - 2δ und 360 - 2δ, weil durch diese vier
Werthe je einer der Factoren gleich Null wird. Es weist also das
Kreisdiagramm für diese vier Drehwinkel keine Abweichung von der
wirklichen Schiebercurve auf, sondern stellt den vollkommenen
Werth aus Gleichung (1) dar.
Das Fehlerglied wird ein Maximum, wenn der erste
Differentialquotient gleich Null wird:
Textabbildung Bd. 220, S. 296
Dieser Gleichung entsprechen vier Werthe: ω = (90 -
δ), (180 - δ), (270 - δ) und (360 -
δ), weil für jeden dieser Drehwinkel einer der Factoren
des Zählers Null wird. Der zweite Differentialquotient zeigt
durch sein Vorzeichen für ω - 90 - δ und 270 -
δ ein Maximum und für ω = 180 - δ und 360 -
δ ein Minimum (negatives Maximum) an.
Figur 10 zeigt in einem Diagramme den Einfluß der
endlichen Länge der Excenterstange (das Fehlerglied) auf die
Schieberbewegung. Auf die horizontale Linie M N wurde die Peripherie des Kreises der
Excentricität Figur 5
abgewickelt und der jeweilig stattfindende Schieberweg OM, das Fehlerglied GH und die wirkliche Function OL nach ihrem Zeichenwerth als Ordinaten
aufgetragen, wodurch man drei Wellenlinien erhält. Die
vollgezogene starke Linie bedeutet den rectificirten
Schieberweg, die gestrichelte Linie stellt das Bewegungsgesetz
bei unendlich langer Excenterstange und die flache, schwach
gezogene Schlangenlinie das Fehlerglied dar.
Der Drehwinkel α, für welchen die Schieberplatte die
Mittelstellung durchläuft, wird mit Rücksichtnahme auf das
Fehlerglied gefunden, indem man f (ξ) = 0 [Gleichung (1)]
setzt und aus dieser Gleichung den Werth ω = α
sucht. Es findet also die Gleichung statt:
Textabbildung Bd. 220, S. 296
woraus sich für sin (α + δ) zwei
Werthe berechnen, welche die beiden Stellungen der Dampfkurbel
bestimmen, wobei der Dampfschieber sich in der Mittellage
befindet. Es ist Textabbildung Bd. 220, S. 296
Construction des
Fehlergliedes am Reuleaux'schen Diagramm.
Das von Reuleaux aufgestellte
Kreisdiagramm eignet sich zur Untersuchung von Steuerungen mit
kurzen Excenterstangen aufs Vollkommenste, nachdem der Einfluß
der endlichen Länge der Excenterstange ganz unmittelbar
ersichtlich gemacht werden kann.
Man verzeichnet dieses Diagramm, indem man Figur 7
den Kreis der Excentricität mit dem Halbmesser OB = r
beschreibt und die Linien RS und DE unter dem Voreilungswinkel SOX = EOY
gegen die beiden Achsen X und Y zieht. Für die allgemeine Lage M unter dem Drehwinkel ω ist aus
dem Dreieck MOH (MH senkrecht RS):
MH = OM sin MOH = r sin (ω + δ) =
s.
Es stellt dieses Perpendikel MH unmittelbar den Schieberweg der
Normaldampfvertheilung ohne Berücksichtigung der endlichen Länge
der Excenterstange dar. Den beirrenden Einfluß des Fehlergliedes
charakterisirt man durch den Kreisbogen KL, welchen man aus dem Punkte D der Linie DE mit der Länge
der Excenterstange durch den Punkt A
beschreibt (BA senkrecht RS), wodurch auf der Strecke MH des Schieberweges unmittelbar das
Fehlerglied HG (abgeschnitten wird.
GM ist somit der wahre Schieberweg
für ω und M′ G′ für 180 + ω als
Drehwinkel.
Man hat also bei Betrachtung des Diagrammes von Reuleaux nur die Linie RS durch den Kreisbogen LK zu ersetzen, um die wahren
Schieberwege zu finden. Man wird daher von D aus die Deckungen mehr den
Canalbreiten zu beiden Seiten auftragen und mit der Länge der
Excenterstange Kreisbögen beschreiben, welche statt der
Parallelen a, a + e, i, e + i
zu setzen sind und alle Fragen vollkommen erledigen.
Zum Beweise fälle man das Perpendikel FG senkrecht DE, wonach
Textabbildung Bd. 220, S. 297
oder, weil GD
= AD = l, FG = r cos (ω + δ) und AO = r cos δ ist:
Textabbildung Bd. 220, S. 297
Positiv, wenn es am Schieberweg, negativ,
wenn es an dessen Verlängerung abgeschnitten wird.
Trägt man das negative Maximum LS
nach N nochmal in den Kreis auf, so
bestimmt ON jene Kurbelstellung, bei
welcher der Schieber die mittlere Stellung durchläuft.
Der Näherungskreis für den Maximalwerth der Function des
Schieberweges wird erhalten, indem man den Mittelpunkt O des Kreises der Excentricität nach C verlegt, ohne die sonstige Behandlung
des Diagrammes zu ändern. Dieser Kreis stellt, wie im Weitern
begründet erscheint, das Bewegungsgesetz der Schieberplatte in
der Nähe des vollen Ausschubes erschöpfend dar.
Für den Entwurf von Schiebersteuerungen weist das Reuleaux'sche
Diagramm den Vortheil auf, daß die Kurbelstellungen für die
Momente der Dampfvertheilung durch vom Mittelpunkt entfernter
liegende Punkte schärfer markirt erscheinen als im Zeuner'schen
Diagramm, obwohl an diesem die Schnittpunkte durch das von E gefällte Perpendikel trotz der
schiefen Schnitte genau bestimmt werden können. Doch liegen bei
jenem alle maßgebenden Punkte am Kreis der Excentricität,
während sie hier mit dem kleinern Ausschub dem Mittelpunkte des
Achsensystemes näher rücken. Der leuchtendste Vorzug der von Zeuner erfundenen Darstellung der
Schieberbewegung ist jedoch, daß sich der Schieberkreis bei
Coulissensteuerungen mit variablem Füllungsgrade unmittelbar der
Verschiebung des Schleifstückes auf eine natürliche Weise anpaßt
und ein treffendes Bild der geänderten Schieberbewegung
gibt.
Näherungskreis für die
Quadrantenstellungen.
Das Zeuner'sche Kreisdiagramm stimmt mit der wirklichen
Schiebercurve für die Drehwinkel 0 und 180, 180 - 2δ und
360 - 2δ vollkommen überein und mag mit Vortheil selbst
bei beeinflussender Länge zur Untersuchung der einfachen
Schiebersteuerung beibehalten werden, wenn die Phasen der
Dampfvertheilung, d. i. das Oeffnen und Schließen der Canäle,
nahezu mit jenen Momenten gleichzeitig eintreffen. Sucht man
geringere, vielleicht nur 50 Proc. Füllung zu erreichen, so wäre
es erwünscht, daß der Schieberkreis die Function des
Schieberweges bei ω = 90 und 270 vollkommen erschöpft und
die todten Punkte beibehalten bleiben.
Textabbildung Bd. 220, S. 298
stellt die wirkliche Schiebercurve dar,
welche sich im Allgemeinen einem Kreise anschließt. Man bestimmt
die Mittelpunktscoordinaten a = OA/2 und b =
OB/2 (Fig. 8)
für den gewünschten Näherungskreis, indem man OA und OB
aus f
(ξ) durch Einsetzen der Werthe ω = 0 und 180, 90
und 270 entwickelt, wobei man erhält:
Textabbildung Bd. 220, S. 298
Man construirt diesen Schieberkreis in
Figur 8, indem man die Linie OE = r unter Voreilungswinkel
YOE = δ zieht und durch den
Endpunkt E aus Punkten
der X- und Y-Achse mit der Länge der Excenterstange die beiden
Kreisbögen EM und EK verzeichnet. Fällt man die
Perpendikel EA und EB, so ist:
OA = r sin δ, OB = r cos
δ,
Textabbildung Bd. 220, S. 299
Trägt man sodann NK = AM auf, so ist OK 2b der
richtige Ausschub für den Drehwinkel ω = 90°. Für
den zweiten Schieberkreis ist ON′ = OB′ - NB, OA′ = OA aufzutragen.
Legt man durch die Punkte AON und
A′ON′ Kreise, so stellen diese die gewünschten
Näherungskreise für die Quadrantenstellungen der Kurbel dar.
Dieses Verfahren ist bei geringer Länge der Excenterstange dann
anzurathen, wenn nahezu halbe Füllung angestrebt wird.
Näherungskreis für den
vollen Ausschub.
Bei der einfachen Schiebersteuerung hält der Dampfschieber die
Einströmungscanäle bei der Mittelstellung geschlossen und
eröffnet dieselben erst bei einer Verschiebung der Platte. Bei
Rost- oder Spaltschiebern ist der Canal bei der Mittelstellung
geöffnet und wird erst durch ein Verrücken der Platte
geschlossen. Treffen beim Muschelschieber die Momente der
Dampfvertheilung vielleicht bei den todten Punkten und bei
ω = 180 - 2δ ein, für welche Stellungen das
Normalkreisdiagramm die geringsten Abweichungen zeigt, so
erfolgt bei Gitterschiebern — wie auch bei Meyer's
Expansionsschieberplatten — das Abschneiden des Dampfes
in der Nähe des vollen Ausschubes, wo das Fehlerglied den
bedeutendsten Einfluß erreicht. Für diese Fälle soll ein
Näherungskreis hergestellt werden, welcher mit der Function des
Schieberweges das Maximum gemeinsam hat und die Schieberbewegung
in der Nähe des vollen Ausschubes vollkommen richtig gibt.
Nachdem die Function
Textabbildung Bd. 220, S. 299
sich im Allgemeinen einem Kreise annähert,
kann der gewünschte Näherungskreis erhalten werden, indem man
über das Maximum der f (ξ) als Durchmesser einen
Kreis verzeichnet. Für den Maximalwerth von ξ muß (dξ/dω) = 0 sein.
Textabbildung Bd. 220, S. 299
Diesen Werth gleich Null gesetzt, geht
ω in den Winkel α über, welchen der Maximalwerth
mit der X-Achse einschließt.
Textabbildung Bd. 220, S. 300
welcher Gleichung durch cos
(α + δ) = 0 Genüge geleistet wird. Es ist demnach
α = 90 - δ und 270 - δ. Bei ersterm Werth
(90 - δ) wird durch das Zeichen des zweiten
Differentialquotienten ein Maximum, bei letzterm (270 -
δ) ein Minimum (negatives Maximum) angezeigt. Den
Durchmesser des Näherungskreises erhält man als den Werth des
Maximums, indem man ω = 90 - δ und 270 - δ
in f
(ξ) einsetzt:
Textabbildung Bd. 220, S. 300
Man zieht Figur 9
den Durchmesser OE nach dem
Normaldiagramm, verzeichnet aus einem Punkte der X-Achse mit der Länge der Excenterstange
den Kreisbogen EM, so ist wie vorher
Textabbildung Bd. 220, S. 300 . EN = E′N′ = AM aufgetragen,
erhält man in ON und ON′ die Durchmesser der
Näherungskreise für den vollen Ausschub.
Endliche Länge der
Triebstange.
Wir wiederholen, daß die Construction des Fehlergliedes sowie die
Anwendung der künstlichen Diagramme der
Praxis nur dann anzu empfehlen ist, wenn durch
Raumverhältnisse die Excenterstange derart kurz bedingt wird,
daß eine Vernachlässigung des hierdurch hervorgerufenen
beirrenden Einflusses zu störenden Abweichungen in der
Dampfvertheilung führen würde; dann ist es auch möglich die
angegebenen Constructionen in Naturgröße oder entsprechendem
Maßstabe durchzuführen. — Hat die Excenterstange eine
solche Länge, daß die Verzeichnung der Kreisbögen nicht
durchführbar ist, so wird deren Einfluß auch keine
Berücksichtigung erfordern, und man behält das Zeuner'sche oder
Reuleaux'sche Diagramm für die Normaldampfvertheilung
unverändert bei. Für Schiffsmaschinensteuerungen hat der
Constructeur immerhin einen Anhaltspunkt, die Anwendung der
durchaus unzweckmäßigen Steuerungsmodelle durch eine graphische
Darstellung der Schieberbewegung zu ersetzen, wobei eine
entsprechende Lehre oder Schablone zum Verzeichnen der
Kreisbögen mit der Excenterstangenlänge mit Leichtigkeit
beigestellt wird. Das Verfahren kann hierbei für die
Stephenson'sche Coulissenumsteuerung direct gebraucht werden,
weil diese bei Schiffsmaschinensteuerungen niemals wegen Dampfersparniß als Expansionsvorrichtung
arbeitet und stets voll eingelegt wird.
Im Uebrigen gilt die Bemerkung Zeuner's, daß „die Unregelmäßigkeiten in der
Kolbenbewegung größern schädlichen Einfluß auf die
Dampfvertheilung haben“, wegen der stets kurzen
Triebstange bei Schiffsmaschinen
Taf. A.
maschinen in noch höherem Maße, und eine
Berücksichtigung dieser Unregelmäßigkeiten ist stets
erforderlich, wozu einige Anhaltspunkte aufgestellt werden
sollen.
Die Dampfvertheilung wurde nur auf den Drehwinkel der
Kolbenkurbel bezogen, ohne zu berücksichtigen, daß zufolge der
endlichen Länge der Triebstange gleichen Winkelabständen der
Dampfkurbel von den todten Punkten ungleiche Kolbenwege
entsprechen, und daß diese auf der Seite der Maschinenachse (bei
directer Triebstange) stets größer sind. Sollte nach dem Vorigen
wirklich eine vollkommen richtige Dampfvertheilung erreicht
worden sein, so daß die entsprechenden Phasen der Canaleröffnung
und Schließung für ω und 180 + ω gleichzeitig
eintreffen, so würden dadurch doch ungleiche Füllungsgrade
bedingt, weil der Dampfkolben für ω und 180 + ω
ungleiche Kolbenwege aufweist.
Faßt man den Kreis der Excentricität Figur 7
zugleich als Kurbelkreis auf, so wäre bei unendlich langer
Triebstange für den Drehwinkel ω die Kurbelwarze in M und der Dampfkolben mit Bezug auf die
Strecke B B′ als Kolbenweg in
T angelangt, wobei OT den Kolbenweg oder den Abstand vom
Mittel des Hubes O und BT, B′T die jeweiligen
Entfernungen von den todten Punkten B und B′ darstellen.
Durch die endliche Länge der Triebstange werden Abweichungen von
der Normalkurbelbewegung hervorgerufen, welche sich nach bereits
entwickelten Anschauungen leicht kennzeichnen lassen.
Man beschreibt mit der relativen Länge der Triebstange [L/R ×
BB′] die Kreisbogen I, II und
III durch die Punkte B′, O
und B aus Punkten der X-Achse. Zieht man durch M eine Parallele P Q zu O X, so ist MN der wirkliche Kolbenweg, MP und MQ
die Abstände des Kolbens von den todten Punkten, wodurch die
Dampfvertheilung direct auf die Kolbenbewegung bezogen wird.
Eine andere Art, die endliche Länge der Triebstange zu
berücksichtigen, besteht darin daß man wie in Figur 11
den Kolbenweg BB′ in eine
entsprechende Anzahl gleicher Theile theilt und die den
Kolbenstellungen 1, 2, 3 ... entsprechenden Stellungen der
Kurbelwarze in I, II, III ...
durch Kreisbögen mit der Länge der Triebstange bestimmt. Die
Phasen der Dampfvertheilung können sodann mit den
Kolbenbewegungen in Uebereinstimmung gebracht werden.
Tafeln