| Titel: | Ueber Herzräder; von Prof. C. W. MacCord. |
| Autor: | C. W. MacCord. |
| Fundstelle: | Band 220, Jahrgang 1876, Nr. , S. 303 |
| Download: | XML |
Ueber Herzräder; von Prof.
C. W.
MacCord.
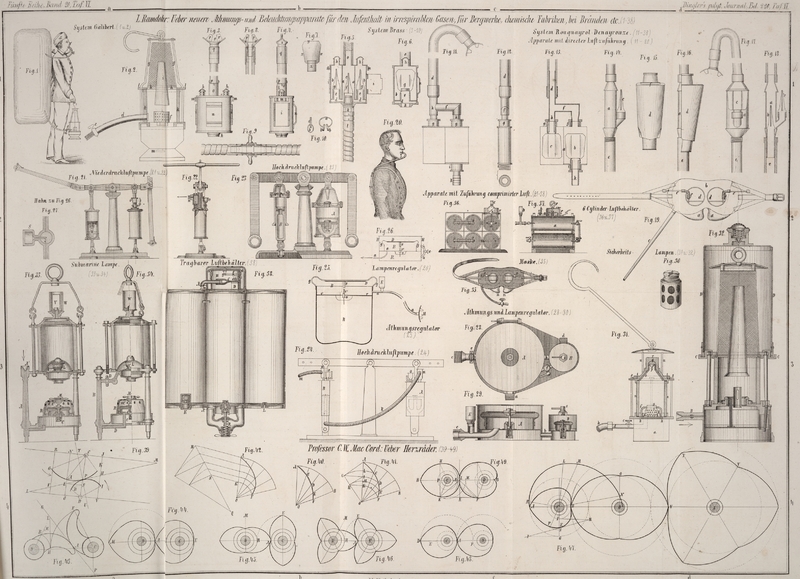
Mit Abbildungen auf Taf. VI.
MacCord, über Herzräder.
Herzräder (unrunde Räder, Spiralräder, englisch lobed wheels) werden in manchen Fällen
angewendet, wenn die gleichförmige Umdrehungsbewegung einer
Welle so auf eine andere übertragen werden soll, daß die zweite
Welle während eines Theiles ihrer Umdrehung sich schneller
bewegen soll als während eines andern. Von solchen Rädern, deren
Außenform durch bekanntere krumme Linien begrenzt wird, wären zu
erwähnen elliptische Räder oder excentrische kreisrunde Räder,
welche mit ovalen zusammengreifen, wie man sie bekanntlich im
Werkzeugmaschinenbau öfters anwendet, um durch die so erlangte
ungleichförmige Bewegung einer Welle die von derselben
hervorgebrachte, an sich sehr ungleichförmige
Kurbelstangenenden-Bewegung in eine nahezu gleichförmige zu
verwandeln.
Zwei gleiche Ellipsen kann man als zu einander passende
Räderformen benützen, wenn man jede Ellipse um einen ihrer
Brennpunkte dreht, und man erhält dann, wenn eine Welle mit
ihrem elliptischen Rade sich gleichförmig einmal umdreht, für
die andere auch eine einzige Umdrehung, aber eine
Umdrehungsgeschwindigkeit, die nach einem bestimmten Gesetz aus
einer Maximalgeschwindigkeit in eine Minimal- und aus dieser
wieder in die Maximalgeschwindigkeit übergeht. Will man mehr als
einen solchen Wechsel während einer Umdrehung erzielen, so kann
man dies durch Herzräder erreichen, welche aus der Ellipsenform
abgeleitet sind. Man ziehe in jeder Ellipse vom Brennpunkte aus
radiale Strahlen und verkleinere die von denselben
eingeschlossenen Winkel in einem bestimmten Verhältniß, auf die
Schenkel der so reducirten Winkel trage man aber die
ursprünglichen Radienlängen auf, so erhält man zwei neue Curven,
die eben so auf einander rollen wie die ursprünglichen Ellipsen.
Es läßt sich dieses Verfahren der Reduction oder Contraction
einer solchen Ellipse auch auf andere gegenseitig auf einander
rollende Curven anwenden, und wenn man ein Paar reguläre
Ellipsen als Einblatträder (unilobed) bezeichnet, so erhält man bei einer Reduction
der Winkel auf die Hälfte Zweiblatträder (twolobed wheels), bei denen die Abwechslung von Maximal-
und Minimalgeschwindigkeit zwei Mal erlangt wird. Eben so lassen
sich Dreiblatt- oder überhaupt Vielblatträder aus der
ursprünglichen Einblattform entwickeln; aber wenn man die
Ellipse als Grundform benützt, so kann man immer nur ein Paar
Einblatträder oder ein Paar Zweiblatträder zusammen arbeiten
lassen, während es vielleicht wünschenswerth ist, ein
Einblattrad mit einem Zweiblatt- oder mit einem Dreiblattrad
zusammen arbeiten zu lassen, weil die getriebene Welle blos halb
oder ein Drittel so schnell laufen soll; eben so kann es
erforderlich sein, ein Zweiblattrad mit einem Dreiblattrad
zusammengreifen zu lassen. Diese Aufgabe läßt sich aber leicht
lösen, wenn man als Curve für die Radform eine logarithmische
Spirale wählt, bei welcher an jedem Punkte der Curve das
Curvenstück oder die Tangente stets den gleichen Winkel mit dem
Radius einschließt. Ist nun auch die Construction solcher
Spiralräder nach der logarithmischen Linie eine längst bekannte
Sache, so ist doch eine mehr elementare und graphische Ableitung
des einzuschlagenden Verfahrens vielleicht Manchem willkommen,
dem die Rechnung mit Logarithmen nicht recht geläufig ist; wir
geben dazu das Nachstehende unter Zugrundelegung einer von Prof.
C. W. MacCord im American Artizan und daraus in der
Deutschen Industriezeitung, 1876 S. 73 veröffentlichten
Arbeit.
Um die Eigenschaften der logarithmischen Curve etwas zu zeigen,
gehe folgende Betrachtung voraus. Es seien (Fig. 39)
RM und LD zwei Parallelen, LM eine
beide Linien schneidende Gerade; CD,
NO, RF,
JH seien andere Parallelen,
senkrecht zu RM, deren Schnittpunkte
mit LM auf F, E, P, und H fallen. Um den Punkt
P werde mit PE als Radius ein Kreisbogen beschrieben und aus C mit einem Radius CA = NE ein
zweiter, welcher den ersten in A
schneidet. Dreht man das Dreieck ACP
so, daß A auf E fällt, so fällt C auf N. Sucht man einen weitern Punkt G so auf, daß man AG = EF, GC = RF
macht, und diesseits CP den Punkt
K dadurch, daß PK = PH, CK = JH
gemacht wird, so kann das entstandene Polygonstück KPAG sich auf die geraden Linien HF abwälzen, und dabei durchläuft der
Punkt C nach und nach die Punkte von
J bis R.
Hätte man die einzelnen Punkte ganz nahe zusammen genommen und
KP, PA
und AG nicht als Sehne, sondern als
Bogenlänge aufgetragen, so würde die gebrochene Linie von K bis G eine
Curve geben, welche im Punkt P von
LM tangirt wird, oder wenn die
Wälzung so erfolgt, daß C nach N kommt, wäre LM die Tangente für den Punkt A. Aus dem Parallelismus von CP und NE folgt aber die
Gleichheit der Winkel NEP und CPM, und es wird also für jeden Strahl,
den man von C aus nach einem
Curvenpunkt zieht, die Tangente an das Strahlende immer den
gleichen Winkel einschließen; demnach ist die Curve eine
logarithmische Spirale und C als
deren Pol zu bezeichnen. Rollt die Curve auf LM hin, so bleibt der Pol immer auf der
Linie RM, und dabei macht jeder
Radius alle Mal mit der Normale zur Berührungsstelle denselben
Winkel, den RM und ML einschließen. Wird dieselbe
Construction auf der andern Seite der Tangente ausgeführt, indem
man PB = PE, DB = OE, PI = PH, DI = VH macht u. s. w., so erhält man eine
andere Curve, deren Pol D ist,
welche ebenfalls auf der Tangente LM
sich abrollt und demzufolge mit der vorigen Curve derart
zusammen arbeiten kann, daß, wenn beide Curven sich um die
festen Punkte C und D drehen, sie sich auf einander
abwälzen, so daß I mit H, E mit A etc. in Berührung kommt. Uebrigens ist
noch zu beachten, daß, wenn man mit BD als Radius den Punkt S
abscheidet und SE zieht, SE senkrecht zu DC wird. PS ist aber die
Differenz der Radien DB und PD, PE die
abgewickelte Bogenlänge; demnach erhält man letztere für ein
durch zwei Radien bestimmtes Stück Curve, wenn man vom Ende des
einen Radius die Radiendifferenz abträgt und in dem so
bestimmten Punkte eine Senkrechte errichtet; diese schneidet
alsdann auf der Tangente die abgewickelte Bogenlänge ab.
Die Verzeichnung der logarithmischen Spirale für einen gegebenen
Radienwinkel AOB (Fig. 40)
kann nun auf verschiedene Weise erfolgen; z. B. man theilt den
Winkel AOB durch Radien in gleiche
Theile, zieht zunächst eine geneigte Linie AC und macht dann die Dreiecke CDO, DEO und
EFO alle ähnlich ACO; die durch die Punkte A, C, D, E, F zu verziehende Curve ist
dann eine logarithmische Spirale, weil sie mit allen Radien
denselben Winkel einschließt. Man erreicht dasselbe, wenn man
(Fig. 41)
an AO eine beliebig geneigte Linie
OG anlegt, zunächst AG senkrecht OG, GI senkrecht AO, IH
senkrecht OG und HK wieder senkrecht zu AO zieht und dann die Radien OC, OD, OE, OF durch Kreisbogen vom
Halbmesser OG, OI, OH, OK begrenzt.
Es handelt sich immer nur darum, ähnliche Dreiecke zu
construiren, und da sich AL : LI = LI :
IM = IM
: MK verhält, so reducirt sich die
Aufgabe dahin, eine gegebene Strecke AK, d. h. die Radiendifferenz OA — OF nach
geometrischem Verhältniß abzutheilen.
Wenn nun Räder construirt werden sollen, so ist meist das
Verhältniß der Winkelgeschwindigkeit des treibenden Rades gegen
die des getriebenen gegeben, und diese verhalten sich umgekehrt
wie die Radien; es würde z. B. (Fig. 39)
v/v′ = PD/CP; v/v″ = DB/AC sein. Außerdem kennt man
den Winkel, um welchen sich jedes Rad drehen soll, während in
dem getriebenen Rade die Maximalgeschwindigkeit in die
Minimalgeschwindigkeit übergeht. Man hätte alsdann nach
Feststellung der Radien, welche in jedem Rade die gleiche
Differenz haben müssen, nur den Winkel AOF (Fig. 42)
für das betreffende Rad aufzuzeichnen, AO und OF die richtigen Werthe
zu geben und KA = OA - OF nach
geometrischem Verhältniß abzutheilen, was man am bequemsten so
macht, daß man erst auf einer beliebigen Linie QR eine Strecke SR, wie früher angegeben abtheilt, diese Eintheilung durch
Parallelen zu AR auf den Radius AO überträgt und die Spirale dann wie
angegeben verzeichnet.
Es sei nun (Fig. 43)
eine Wellenentfernung CD gegeben; es
sollen beide Wellen sich um gleiche Winkel drehen, aber das
Uebersetzungsverhältniß für die größte Winkelgeschwindigkeit der
getriebenen Welle AD/AC und für die kleinste die Reciproke
AC/AD
sein, so ist CD nach Verhältniß AD : AC
abzutheilen, DH = AC zu machen und für die Winkel MDA = ECH,
sowie für die Radiendifferenz AH die
logarithmische Spirale aufzuzeichnen. Errichtet man in H eine Senkrechte HL zu DC und schneidet von A aus mit AC
gleich der ausgestreckt gedachten Bogenlänge AE = AB den
Punkt L ab, so gibt GLAP die Lage der Tangente.
Als specielle Fälle seien hierbei (Fig. 44)
einfache Herzräder anzuführen, für welche der Winkel MDC = 180° ausfiele und die
Spirale symmetrisch zu beiden Seiten von AE aufzuzeichnen wäre.
Wird der Winkel MDC = 90°
genommen (Fig. 45),
so lassen sich Zweiblatträder durch vierfache Aneinanderreihung
von auf- und absteigenden Spiralen zusammensetzen. Für
Dreiblatträder mit dreimaliger Abwechslung der Geschwindigkeiten
für einen Umgang (Fig. 46)
hätte Winkel MDC 60° zu
betragen. Soll aber die treibende Welle blos einen Umgang
machen, während die getriebene deren zwei macht (Fig. 47),
so ist zunächst für einen Winkel von 180° und eine
Radiendifferenz ein Herzrad zu construiren und kann dessen
Spirale gleich weiter fortgesetzt aufgezeichnet werden. Das
getriebene Rad wird dann ein Zweiblattrad, für welches der
Winkel der Radien BD und DO blos 90° beträgt und die
Radiendifferenz BD - DO = AC -
BC = FG
sein muß. BD und DO sind aber erst zu bestimmen, und zwar
werden beide in demselben Verhältniß größer als AC und BC
ausfallen, als die Radiendifferenz FG größer als der Werth EG
ist; es müßte also BD : AC = FG :
GE oder BD = AC . FG/GE sein
und DO = BD - FG. Man könnte aber auch
an C einen rechten Winkel LCK anlegen und so lange in der Spirale
sich drehen lassen, bis die Differenz der Schenkel LC - KC =
AC - BC
ausfällt, dann wäre DB = LC und DO =
KC zu nehmen.
Es lassen sich beide Radien aber noch auf andere Weise ermitteln;
setzt man LC = x und KC =
y, sowie der Kürze halber AC = a und
BC = b
so würde EC = √a b nach der frühern Entwicklung sein.
Nun soll x - y = a - b, also y = x - a + b sein, und es muß x : y = a : √a
b sich verhalten oder x : (x - a + b) = a :
√a b, woraus
x√a
b = ax + a2 + ab
x(√a
b - a) = ab - a2
Textabbildung Bd. 220, S. 307
und y = b
+ √a b = BC + EC.
Also sind die gesuchten Radien BD und
DO einfach aufzufinden, indem man
den Radius CE an AC und CB
ansetzt, und läßt sich dann das Zweiblattrad leicht vollenden.
Wollte man das construirte Herzrad mit einem Dreiblattrad
zusammenarbeiten lassen, so daß die getriebene Welle blos ein
Drittel so viel Umgänge machte als die treibende, oder sollte
das Zweiblattrad mit einem Dreiblattrad zusammengreifen und
letzteres dann blos zwei Drittel so viel Umgänge machen als das
Zweiblattrad, so würde man wieder von dem Herzrade ausgehen, an
AC den Winkel ACP = 60° anlegen und, mit CP einen Kreisbogen beschreibend, die Differenz SG bestimmen. Dann würde der große
Radius des Dreiblattrades TU sich
wieder bestimmen lassen ähnlich wie früher: TU = AC. GF/SG, und
der kleinere: UV = TU - FG oder
= CP. FG/SG . Oder man hätte an C einen Winkel NCM von 60° anzulegen, dessen Schenkel wieder um
FG verschieden lang sind.
Es ist nun leicht zu übersehen, in welcher Weise man das
Verfahren fortsetzen könnte. Dabei ist noch zu erwähnen, daß,
wenn man das Herzrad verzahnen will, man blos nöthig hätte, die
Strecke FG in so viel gleiche Theile
zu theilen, als man auf jeder Spirale Zähne anzubringen
beabsichtigt; die durch die Theilpunkte beschriebenen
concentrischen Kreisbogen schneiden dann auf der Spirale gleiche
Bogenlängen ab. Es läßt sich der Beweis für die Richtigkeit
dieses Verfahrens leicht aus Figur 39
ersehen, denn die Theile EH und HI der Tangente am Punkt E (Fig. 47),
die durch die Senkrechten HF und GI abgeschnitten werden, sind die
Bogenlängen EB und EA, also die Abtheilungen der Curve
proportional denen der Tangente und diese wegen des
Parallelismus von FH und IG proportional denen von FG.
In Einblatt- oder Herzrädern läßt sich auch die Ellipse mit der
Spirale combiniren; es läßt sich z. B. ohne Weiteres einsehen,
daß die eine Hälfte des Rades (Fig. 48)
nach einer aufsteigenden Spirale, die andere nach einer
Halbellipse geformt werden kann. Die Grenzumsetzungsverhältnisse
sind dann dieselben, aber die Uebergänge aus einer
Geschwindigkeit in die andere erfolgen für die beiden halben
Umdrehungen nach verschiedenen Gesetzen.
Es lassen sich überhaupt die mannigfaltigsten Formen von Rädern
combiniren, derart, daß in einzelnen Sectoren Spiralen
zusammenarbeiten, in andern aber Ellipsen, entweder volle oder
nach gewissen Winkelverhältnissen contrahirte. Dabei wird
freilich immer das Minimalumsetzungsverhältniß die Reciproke des
Maximalumsetzungsverhältnisses sein, und es kann in besondern
Fällen wünschenswerth sein, daß dies nicht der Fall ist. Zwei
zusammengehörige Herzräder lassen sich nun auch in folgender
Weise ausführen (Fig. 49).
Es sei C der Pol einer Spirale,
welche mit einer andern, deren Pol sich in D befindet, zusammenrollt. Beschreibt
man mit DM = CM Kreisbogen, so schneiden diese die Spiralen in den
Punkten E und F, und es sind die Bogenlängen AE, GF, BE und AF alle gleich. Da CE gleich und parallel DF ist, so sind dies auch EF und CD.
Errichtet man im Halbirungspunkte K
eine Senkrechte, so ist LE = LF; CE = EK und PE
senkrecht auf EF gibt in P den Mittelpunkt einer Ellipse, für
welche PL die große, PE die kleine Halbachse und C der Brennpunkt ist. Da PL = EK =
½EF = ½CD, so kann D der Brennpunkt einer gleichen Ellipse werden, welche die
erste in L berührt und mit ihr
rollt. Für die ursprünglichen Spiralbogen EA und AF kann man also
Ellipsenquadranten LE und EF substituiren, so daß nach einer
halben Umdrehung auf den Eingriff der Spirale derjenige der
Ellipse folgt. Bei jeder Umdrehung findet daher das
Maximalumsetzungsverhältniß BC : DG und das Minimalumsetzungsverhältniß
CL : CD
statt. Da der Spiralbogen EB = EA ist, so folgt aus der Natur dieser
Linie, daß die Sehne EB größer als
Sehne EA, also auch BP größer als PA und CL größer als CA ist. Die Größe der Verschiedenheit
hängt allerdings vom Verhältniß BC
zu CA ab, also von der
Maximalübersetzung, und es ist nicht gut möglich, die Grenze der
Veränderung ohne Weiteres vorauszusehen.
EF ist wohl Tangente der Ellipse,
aber nicht für die Spirale; also werden die beiden
zusammenstoßenden Curven nicht ohne eine kleine Brechung in
einander übergehen, was aber nichts schaden wird, wenn die Räder
verzahnt werden.
Tafeln