| Titel: | Ueber die Ochwadt'sche Steuerung; von Prof. Hanner in Wien. |
| Autor: | Hanner |
| Fundstelle: | Band 222, Jahrgang 1876, S. 20 |
| Download: | XML |
Ueber die Ochwadt'sche Steuerung; von Prof. Hanner in Wien.
Mit Abbildungen auf Taf.
I [a/1].
Hanner, über die Ochwadt'sche Steuerung.
Vor kurzem wurde in diesem Journale (* 1876 220 396) von
Ingenieur Müller-Melchiors die Ochwadt'sche
Expansionssteuerung beschrieben. Da dieser Fachmann nicht darauf einging, die
genannte Steuerung durch das Diagramm zu untersuchen, so sei es nun gestattet, über
letzteres zu sprechen, wobei die frühern Abbildungen (Fig. 17 bis 18 Band 220 Tafel
VII) zu Grunde gelegt werden sollen.
Die hier in Anwendung kommenden Bezeichnungen sind:
ρ Excentricität,
α Voreilwinkel des Vertheilungsexcenters,
w₁ Drehwinkel der Dampfkurbel während der
Volldruckperiode,
ξ₁ Entfernung des Mittels des
Vertheilungsschiebers vom Mittel des Schieberspiegels (Dampfauslaßcanals) in dem
Augenblicke, wo die Expansion beginnt,
2λ lichte Entfernung der
beiden Hebel a und a',
2μ Entfernung der beiden
Nasen n und n',
2x äußere Entfernung der zum
Anstoße kommenden Auslöser p und p', endlich
e äußere Ueberdeckung des Vertheilungsschiebers.
Wir müssen hier zwei Fälle unterscheiden, je nachdem nämlich w₁ < 90 – α oder
w₁ > 90 – α ist.
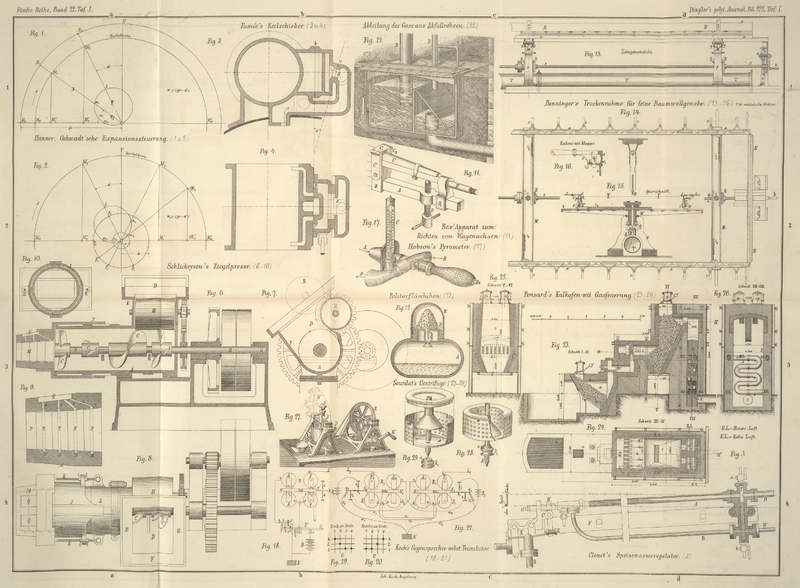
I) w₁ < 90 – α. Man construire (Fig. 1) nach der bekannten
Regel das Zeuner'sche Diagramm für den Vertheilungsschieber und verzeichne alsdann
einen Kreis vom Mittelpunkte O und Halbmesser ON₀ = μ. Gibt
nun M₁O die
Kurbelstellung in dem Momente an, wo die Expansion durch den Expansionsschieber
beginnen soll, so repräsentirt die Größe 2 N₁ m₁ die äußere Entfernung 2x der Auslöser p und p', welche diesem Expansionsgrade ε =
M₀ M₁'/M₀ M₀'
entspricht; d.h. es ist dann einfach
x = N₁ m₁.
Der Beweis für die Richtigkeit des eben Vorgeführten ist höchst einfach. Bei Beginn
der Expansion stößt nämlich in diesem Fall p' an n, und zwar erfolgt dieser Anstoß noch während der
Rechtsbewegung des Vertheilungsschiebers. Da nun p und
p' die Bewegung des Vertheilungsschiebers besitzen,
so muß hier
μ = x + ξ₁
sein, woraus sofort folgt
x = μ – ξ₁ = N₁ O – m₁ O = N₁ m₁ (1)
was zu beweisen war. Man erkennt nun leicht, daß für x = N₀ m₀ der Winkel w₁ = 0 und für x = N₂ A der Winkel w₁ = 90 – α wird. Nach
dem Diagramm kann man also während der Rechtsbewegung des Vertheilungsschiebers alle
Expansionsgrade von ε = 0 bis ε = M₀ M₂'/M₀ M₀' erreichen, wenn man nur x innerhalb der Grenzen N₀ m₀ und N₂ A zweckdienlich verändert.
II) w₁ > (90 – α). Anders verhält sich die Sache in dem zweiten Fall, wo nämlich
die Expansion durch den Auslöser erst bei der Retourbewegung des
Vertheilungsschiebers eingeleitet werden darf. Nehmen wir wieder an, daß Kolben und
Vertheilungsschieber nach rechts sich bewegen, so muß jetzt bei Beginn der Expansion p an a anstoßen, aber erst
dann, wenn die Linksbewegung des Vertheilungsschiebers erfolgt. Dabei befindet sich
das Vertheilungsschiebermittel noch rechts vom Mittel des Schieberspiegels. Weil
jedoch die Auslöser und der Vertheilungsschieber eine vollkommen gleiche Bewegung
besitzen, so ist λ = x – ξ₁, also
x = λ + ξ₁
(2)
Construirt man (Fig. 2) wieder das
Zeuner'sche Diagramm für den Vertheilungsschieber und verzeichnet noch einen Kreis
vom Mittelpunkte O und Halbmesser P₀ O = λ, so gibt für den Expansionsgraden ε = M₀ M₁'/M₀ M₀' die Größe 2 P₁ m₁ die Entfernung der beiden Auslöser p und p' an; d.h. es ist
x = P₁ m₁.
Die Richtigkeit dieser Behauptung folgt sofort, wenn man
bedenkt, daß
Om₁ = ξ₁ und P₁ O = λ, daher P₁ m₁ = λ + ξ₁
= x.
Wir sehen also, daß man mittels der Ochwadt'schen Steuerung auch höhere Füllungen
erreichen kann, wenn man nur die Auslöser einander entsprechend nähert. Die größte
Füllung wird dann erzielt, wenn man x = P₁ m₁ macht,
wobei m₁ jenen Punkt bezeichnet, wo der
Ueberdeckungskreis vom Halbmesser On₀ = e den obern Schieberkreis durchschneidet. In diesem
Falle hat der Expansionsschieber gar keinen Einfluß mehr auf die Dampfvertheilung,
die Expansion wird blos durch den Vertheilungsschieber allein hervorgebracht, die
Füllung im Cylinder ist ein Maximum. Diese Steuerung gestattet also alle
Expansionsgrade von ε = 0 bis ε = M₀ M₁'/M₀ M₀' (also ε =
0,05 bis 0,80) zu erreichen.
Schließlich sei noch bemerkt, daß die Excentricität keine ganz willkürliche Größe
ist, sondern von den Dimensionen λ und μ abhängt. Für w₁ = 90 – α folgt nämlich,
wegen ξ₁ = ρ, aus Gleichung (1)
x = μ – ρ
und aus Gleichung (2)
x = λ + ρ, daher
λ + ρ = μ – ρ und
ρ = 1/2 (μ – λ)
(3).
Tafeln