| Titel: | Einwirkung der Raschheit der Formänderung auf die Widerstandsfähigkeit der Materalien; von Prof. R. H. Thurston. |
| Fundstelle: | Band 223, Jahrgang 1877, S. 333 |
| Download: | XML |
Einwirkung der Raschheit der Formänderung auf die
Widerstandsfähigkeit der Materalien; von Prof. R. H. Thurston.
Mit Diagrammen auf Tafel
B.
Thurston, über die Widerstandsfähigkeit der
Materialien.
Von Seite des Verfassers wurde bereits des nach Tresca so
genannten „Flusses der Metalle“ in Bezug ihres die
Widerstandsfähigkeit der Metalle gegen äußere Beanspruchung modificirenden
Einflusses gedacht.Transactions of the American Society of Civil
Engineer, Bd. 3 S. 13.
Dieselbe moleculare Bewegung, oder Fluß, welche die innern Kräfte wieder ausgleicht
und die innern Spannungen mildert, ist möglicherweise nur eine Phase jener
Eigenschaft, von welcher Vicat voraussetzte, sie könne
nach Verlauf einer gewissen Zeit den Bruch eines Metalles herbeiführen, wenn selbes
einer nahezu seiner Festigkeitsgrenze entsprechenden Belastung ausgesetzt wird. Die
eine dieser Actionen ist mehr unmittelbar als die andere; letztere bringt ihre
Wirkung hervor, selbst wenn die Cohäsionskraft wirklich gesteigert worden wäre.
Es wurde übrigens beobachtet, daß in allen jenen Fällen, in welchen Schmiedeisen und
Stahl einer Beanspruchung über die Elasticitätsgrenze ausgesetzt wurden, sie keine
Neigung zum „Fließen“ zeigten, und daß beinahe in jedem dieser
Fälle eine thatsächliche und bleibende Erhöhung der
Elasticitätsgrenze durch Spannung Platz griff. Weiters wurde bei keinem der
gemachten Versuche an einem und demselben Stücke ein gleichzeitiges Vorkommen des
Fließens und der Erhöhung der Elasticitätsgrenze durch Spannung beobachtet.
Seither an Kupfer vorgenommene Experimente ergaben autographische Spannungsdiagramme,
an denen sich dieser doppelte Effect beobachten ließ. Die Erhöhung der
Elasticitätsgrenze trat während der ersten Periode des Experimentes ein, in einer
darauf folgenden spätern Periode zeigte das Diagramm Fluß, wobei das Metall bei
allmälig abnehmendem Widerstande nachgab. Dieses Phänomen sinkenden Widerstandes bei
zunehmender Verdrehung, welches bei Eisen und Stahl vor dem Bruch nie eintrat, wurde
seither häufig an andern Materialien wahrgenommen.
So z.B. geben die folgenden zwei Tabellen I und II einige Illustrationen hierzu.
I. Torsionsversuche.In den nachstehenden Tabellen bezeichnet zur Abkürzung T = Tag, St = Stunde und M =
Minute.Die Red.
Nummerder Probe.
Materialtheile.
Dauer derInanspruchnahme.
Torsionswinkel.
Sinken desStiftes.
Anmerkungen.
Zinn
Kupfer.
Grad.
Zoll.
mm.
Dasselbe Stück
123
100,00100,00100,00
–––
40 M 1 St 2 St
65180280
0,060,100,10
1,522,542,54
Erholte sich nach weiterer Verdrehung um
1°, woder Stift wieder auf die ursprüngliche Höhe
stieg.Desgl. nach 8°.Desgl. nach 80°.
4
99,44
0,56
12 M
380
50 Procent
Erholte sich nicht wieder.
5
98,89
1,11
–
–
–
–
Verhielt sich wie Nr. 4.
6
Legirung
–
58
0,2
5,08
Erholte sich nicht wieder.
II. Versuche mit transversalem Zug bei ruhiger Belastung.
Probestücke 1 × 1 × 22 Zoll (25,4 × 25,4 × 558mm,8).
Nummerder Probe.
Materialtheile.
Belastung.
Durchbiegung.
Zeit
Zunehmende Durchbiegung.
Bruchbelastung.
Zinn.
Kupfer.
Pfd.
k
Zoll.
mm.
Zoll.
mm
Pfd.
k
7
–
100,00
600
272,16
0,534
13,56
5 M
0,009
0,23
650
294,84
8
1,90
98,10
475
215,46
1,762
44,75
3 „
0,291
7,39
–
–
500
226,80
2,108
53,54
3 „
0,488
12,40
500
226,80
9
7,20
92,80
950
430,92
0,348
8,84
5 „
0,081
2,06
1350
612,36
10
10,00
90,00
950
430,92
0,395
10,03
5 „
0,021
0,53
–
–
1485
673,60
3,447
87,55
13 „
4,087
103,18
1485
673,60
11
90,30
9,70
100
45,36
0,085
2,61
10 „
0,021
0,53
–
–
120
54,43
0,140
3,56
10.„
0,055
1,40
–
–
140
63,50
0,221
5,61
10 „
0,098
2,49
–
–
„
„
0,319
8,10
10 „
0,038
0,97
–
–
„
„
0,357
9,07
40 St
0,920
23,38
–
–
160
72,58
1,294
32,87
10 M
0,025
0,63
–
–
„
„
1,320
33,53
1 T
1,000
25,40
–
–
„
„
2,320
58,93
1 „
1,000
25,40
–
–
„
„
3,320
84,33
1 „
1,000
25,40
160
72,58
12
98,89
1,11
90
40,82
0,243
6,17
5 M
0,063
1,60
–
–
120
54,43
0,736
18,69
15 „
1,055
26,80
–
–
„
„
1,791
45,49
30 „
0,748
19,00
–
–
„
„
2,539
64,49
45 „
0,595
15,11
–
–
„
„
3,134
79,60
12 St
8,000
203,20
120
54,43
13
100,00
–
80
36,29
0,218
5,54
5 M
0,064
1,63
110
49,90
Zwischen diesen Extremen der Zusammensetzung liegende Metalle ließen bei constanter
Belastung Fluß oder zunehmende Durchbiegung nicht an sich beobachten.
Versuche über die Zugfestigkeit ähnlicher Metalle weisen analoge Resultate auf, und
es scheinen diese Versuche und die dabei gemachten Beobachtungen die oben gemachten
Bemerkungen zu bestätigen und anzuzeigen, daß unter gewissen Bedingungen die
Erscheinung des Fließens und die Erhöhung der Elasticitätsgrenze durch Spannung
co-existirend seien, wie dies speciell bei zähen, faserigen Substanzen zu
beobachten ist.
Eine weitere Schlußfolgerung in unserer oben angezogenen Abhandlung bezieht sich auf
ein für Schmiedeisen abgeleitetes Gesetz, welches, wenn wirklich bestehend, von noch
größerer Wichtigkeit für den Ingenieur ist, als die eben angeführten Thatsachen,
nämlich: daß die Zeitdauer, während welcher die Inanspruchnahme stattfindet, von
entscheidendem Einfluß auf deren Effect ist, nicht blos als ein Factor, der die
lebendige Kraft der belastenden und die Trägheit der widerstandleistenden Masse
modificirt, sondern auch durch die Einflußnahme auf die Hervorbringung und
Vertheilung der innern Spannungen.
Es wurde an der Hand autographischer Spannungsdiagramme erwiesen, daß einige
Materialien um so leichter nachgeben, je rascher Verdrehung und Bruch hervorgebracht
werden, wobei der Widerstand als in verkehrtem Verhältnisse mit der Raschheit der
Formänderung stehend befunden wurde. Weiters wurde die Vermuthung aufgestellt, daß
diese Wirkung nahe verwandt sei dem entgegengesetzten Phänomen, nämlich der Erhöhung
der Elasticitätsgrenze durch Spannung. Eine Erklärung hierfür bot sich aus der
Annahme, daß bei rapider Verdrehung nicht genügend Zeit bleibt zur Milderung der
innern Spannung. Ferner wurde bemerkt, daß die dehnbarsten Substanzen, wenn durch
Stoß oder anderweitige rapide Wirkung gebrochen, ähnliches Verhalten zeigen können
wie verhältnißmäßig spröde Substanzen.
Seither wurden die experimentellen Untersuchungen mit zeitweiligen Unterbrechungen
fortgeführt, wobei sich die oben angeführten Behauptungen bestätigten, und wobei
sich herausstellte, daß zwischen diesen Spannungserscheinungen und der Zeitdauer der
Inanspruchnahme Beziehungen bestehen, welche hier als Ergänzung der bereits
publicirten Gesetze angeführt werden sollen. Sollte sich, wie der Verfasser
voraussetzt, bewahrheiten, daß die Ursache der abnehmenden Widerstandsfähigkeit, wie sie manchmal bei gesteigerter Raschheit der Verdrehung beobachtet wurde, in naher
Verwandtschaft steht zur Erhöhung der Elasticitätsgrenze durch Spannung, so würde
sich folgender Satz als einfacher Ergänzungssatz hinstellen lassen:
„Unelastische und faserige Materialien, welche unfähig sind, während
einer Verdrehung innerlich gespannt zu werden, müssen größern Widerstand gegen
rapid hervorgebrachte Verdrehung, wie gegen allmälig und langsam hervorgebrachte
äußern, und zwar in Folge ihrer Unfähigkeit, die innere moleculare
Zusammensetzung, resp. den Querschnitt schnell genug zu verändern“ .
Dieses Gesetz zeigte sich bei einer großen Anzahl von Versuchen als richtig und ist
vielleicht von allgemeiner Geltung. Kupfer, Zinn und andere unelastische und
dehnbare Metalle und Legirungen zeigen dieses Verhalten und sind in dieser Beziehung
Gegensätze zu Schmiedeisen und Stahl.
Der Verfasser erwähnte der Thatsache, daß sehr weiches Eisen nicht immer eine
wahrnehmbare Erhöhung der Elasticitätsgrenze durch Spannung aufweist, und Commodore
L. A. Beardslee der Vereinigten Staaten-Marine hat
unlängst beobachtet, daß das weichste und dehnbarste Probestück von Eisen, welches
je von ihm auf der Werfte zu Washington geprüft wurde, eine wahrnehmbare Steigerung der Widerstandsfähigkeit bei wachsender
Raschheit der Inanspruchnahme zeigte. Dieses Metall war besonders eigenthümlich in
seiner Weichheit und extremen Dehnbarkeit. Alle übrigen im Handel vorkommenden
Eisensorten scheinen zur andern Klasse zu gehören. Ebenso geben die Untersuchungen
im mechanischen Laboratorium des Stevens Institute of
Technology zu Hoboken zahlreiche Illustrationen zur Behauptung, daß
Metalle, welche bei constanter Belastung allmälig nachgeben, bei gesteigerter
Einwirkungsgeschwindigkeit erhöhte Widerstandsfähigkeit bieten. Die Biegungscurven
einer beträchtlichen Anzahl dehnbarer Metalle und Legirungen verlaufen
continuirlich, wenn die Zeitintervalle, während welcher die einzelnen Belastungen
nach einander zur Wirkung kamen, gleich warm; sobald aber diese Zeitintervalle
variirten, zeigen sich Unregelmäßigkeiten im Verlaufe der Curve. Probestücke von
solchen Metallen, gebrochen durch transversalen Zug, setzten rapid wirkenden Kräften
einen größern Widerstand entgegen als bei langsamer Steigerung. Zwei einer und
derselben Stange entnommene Probestücke aus Zinn wurden durch transversalen Zug zum
Brechen gebracht, das eine durch rapide und das andere durch allmälig stattfindende
Einwirkung; das erstere Probestück ertrug bis zum Brechen eine Belastung von 2100
Pfd. (952k,5), das zweite 1400 Pfd. (635k). Dieses Beispiel ist geeignet, die große
Differenz zu beleuchten, welche in ähnlichen Fällen eintreten kann, und es scheint
dem Verfasser die Möglichkeit dessen anzuzeigen, daß in extremen Fällen Resultate
erhalten werden, die im höchsten Grade trügerisch sind, sobald auf die Zeit keine
Rücksicht genommen wird. Die über diese Klasse von Metallen genommenen autographischen
Spannungsdiagramme zeigen auf lange Strecken hin sanft verlaufende, gerade und
horizontale Linien, wenn die Verdrehung mit gleichförmiger Geschwindigkeit
stattfindet. Steigerung der Schnelligkeit der Verdrehung verursacht ein
unverzügliches und anhaltendes Steigen des Stiftes, und eine Abnahme dieser
Schnelligkeit verursacht ein Hinabsinken der Linie. Bei einigen Experimenten blieb
der Stift in einer horizontalen Linie, wenn während einer halben Stunde die
Verdrehung einer vollen Umdrehung gleichkam.
Zwei Versuchstücke wurden ein und derselben Stange entnommen, eines davon rasch, das
andere langsam zum Bruche gebracht; ersteres gab im Spannungsdiagramm eine um 50
Fußpfund (6mk,91) höhere Maximalordinate
als letzteres, die Differenz betrug beinahe 50 Proc.
Es ist augenscheinlich daß, wie immer auch der Charakter des Metalles und die
Schnelligkeit des Brechens sei, doch die Wirkung der Trägheit der Masse und der
durch den Stoß nicht unmittelbar getroffenen Partikeln bestehen bleibt und stets
eine Verminderung der Widerstandsfähigkeit gegen Stoß hervorbringt, welche in vielen
Fällen das durch die oben angeführte Gründe bedingte Wachsen der
Widerstandsfähigkeit mehr als ausgleichen kann.Die Trägheit des Gewichtes in der Festigkeitsmaschine hat in diesen Fällen
einen unmeßbar geringen Einfluß auf die Modificirung der Resultate.
Der Verfasser würde demnach die Metalle in zwei Klassen eintheilen, nämlich:
1) Metalle, die in Folge künstlicher Bearbeitung innerer Spannung
ausgesetzt sind. Diese zeigen Erhöhung der
Elasticitätsgrenze durch Spannung und abnehmende Widerstandsfähigkeit bei zunehmender Schnelligkeit der Verdrehung. Das
gewöhnlich im Handel vorkommende Eisen kann als Typus dieser Klasse angesehen
werden.
2) Metalle von unelastischem faserigem Charakter, welche innerer
Spannung nicht ausgesetzt sind. Diese zeigen im Allgemeinen keine Erhöhung der
Elasticitätsgrenze durch Spannung, dagegen bei zunehmender
Geschwindigkeit der Verdrehung erhöhte Widerstandsfähigkeit. Als Typus dieser Klasse kann Zinn betrachtet
werden.
Es ist klar, daß für die Constructionen des Ingenieurs die Metalle der ersten Gruppe
einen weitaus größern Werth besitzen als jene der zweiten, besonders bei permanenten
Belastungen und geringen Sicherheitscoefficienten.
Die Herabminderung der Elasticitätsgrenze durch andauernde Belastung wurde an gewissen Materialien
schon früher bemerkt, ohne jedoch genügende Betrachtung zu finden. Das beigefügte
Täfelchen B zeigt die
Spannungsdiagramme, zusammengestellt nach den Resultaten der Experimente. Sie wurden
als typische Beispiele für die obenerwähnten zwei Gruppen von Metallen ausgewählt.
Zur Vornahme der Experimente wurde das Probestück in zwei cylindrische Stahllager
eingespannt, welche von einer genau gehobelten horizontalen Platte getragen wurden.
Die Biegung wurde hervorgebracht durch eine kräftige Schraube und ein großes
Handrad. Die Belastung wurde durch eine Fairbank'sche Wage gemessen und die Biegung
sowie die Setzung mit einem speciellen von Brown und Sharp angefertigten Meßapparat bestimmt, welcher ein
Ablesen bis zu 0,0001 Zoll (0mm,25)
gestattete; der Meßapparat wurde von den auf den Biegungsapparat einwirkenden
Kräften nicht afficirt. Die Belastung oder biegende Kraft wurde mit Hilfe des
Wagebalkens adjustirt. Nachdem das Probestück eingespannt war, wurde das zur
Verwendung kommende Gewicht an dem Wagebalken hinausgeschoben und die Schraube
sorgfältig gedreht, bis durch ihren Druck auf die Mitte des Probestückes der
Wagebalken sich langsam hob und beiläufig in der Mitte seines Spieles schwankte, was
durch einen am Ende des Balkens angebrachten und längs einer feingetheilten Scale
spielenden Zeiger angezeigt wurde. Bei richtigem Einspielen wurde die Biegung
abgelesen, und der Wagebalken der Belastung entledigt, um die Setzung abmessen zu
können. Hierauf wurde das Probestück durch stärkere Belastung weiter gebogen.
Gelegentlich wurde das Probestück belastet gelassen und das von demselben geäußerte
Widerstandsvermögen in häufig auf einander folgenden Intervallen gemessen. In allen
solchen Fällen senkte sich der Wagebalken allmälig, und eine Abnahme des
Wiederherstellungsvermögens im Probestücke wurde beobachtet. Nach dem Sinken des
Wagebalkens wurde das Gewicht so weit zurückgeschoben, als nothwendig war, um ihn
beiläufig wieder in seiner Mittelstellung einspielen zu lassen, wobei das wirkende
Gewicht und die Zeitintervalle notirt wurden. Bei Wiederholung dieses Vorgehens
zeigte der Hebel einen successive geringer werdenden Verlust im
Wiederherstellungsvermögen des Probestückes an, bis der genügend erleichterte
Wagebalken endlich in seiner Stellung verharrend blieb, worauf eine neue Reihe von
Versuchen vorgenommen wurde.
Das Probestück Nr. 599 bestehend aus 90 Th. Zink, 10 Th. Kupfer zeigt (Tafel B und Tabelle III S.
340) ein constantes Verhältniß zwischen der wirkenden Kraft und der durch dieselbe
hervorgebrachten Verdrehung; der verschwächende Einfluß dauernder Belastung
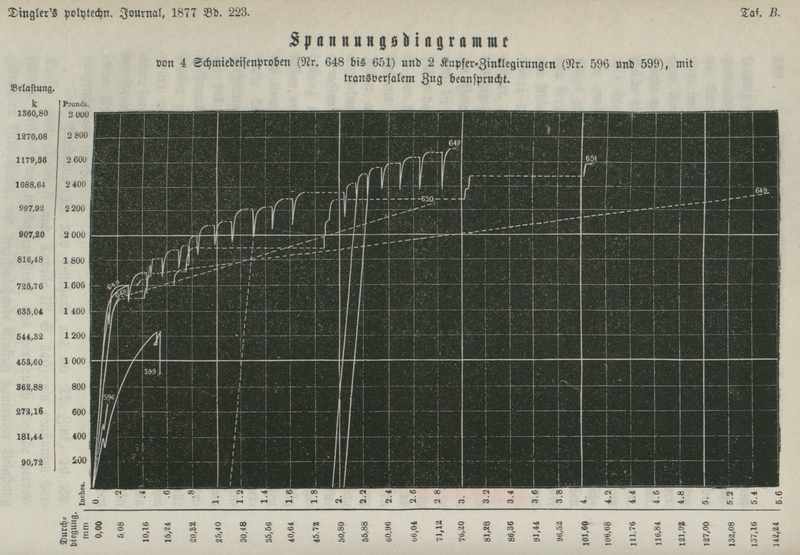
Taf. B. Spannungsdiagramme von 4 Schmiedeisenproben (Nr.
680 bis 651) und 2 Kupfer-Zinklegirungen (Nr. 596 und 599), mit
transversalem Zug bensprucht. S. 338–339
ist in den Unterbrechungen der Curve wohl ersichtlich; bei
erneut wachsender Inanspruchnahme dagegen setzt sich die Curve stets wieder in dem
ursprünglichen Sinne fort. Der durch dauernde Belastung hervorgebrachte Verlust an
„Wiederherstellungsvermögen“ belief sich bei einer
Belastung von 163 Pfd. (73k,94) auf 20 Pfd.
(9k,07), die Durchbiegung betrug 0,0347
Zoll (0mm,88). Hierauf wurde das Probestück
bis auf 3 Pfd. (1k,36) entlastet und zeigte
eine bleibende Setzung von 0,0039 Zoll (0mm,099). Bei 403 Pfd. (182k,80) war
der Verlust an Wiederherstellungsvermögen so ziemlich derselbe, wie dies aus der
Tabelle III zu ersehen ist. Zuletzt wurde die Belastung auf 1233 Pfd. (559k,29) gesteigert bei entsprechender
Durchbiegung von 0,5209 Zoll (13mm,23).
Nach 15 Minuten, während welcher die Durchbiegung constant erhalten wurde, hatte die
Belastung successive auf 1137 Pfd. (515k,74) herabgesetzt werden müssen. Bei der nun folgenden gänzlichen Entlastung
auf 3 Pfd. (1k,36) zeigte sich eine
bleibende Setzung von 0,2736 Zoll (6mm,95).
Nun wurde die Belastung neuerdings auf 1233 Pfd. (559k,29) gebracht – Durchbiegung 0,5456
Zoll (13mm,86) – und der
„Zeitversuch“ wiederholt. Das erhaltene Resultat war ein
ganz unerwartetes. Das Wiederherstellungsvermögen nahm in
wechselndem Betrage beständig ab, endlich brach das Probestück scharf entzwei und
die zwei Hälften fielen zu Boden. Das Wiederherstellungsvermögen war bis auf 911
Pfd. (413k,23) gefallen. Die Durchbiegung
war genau dieselbe wie bei 1233 Pfd. (559k,29) Belastung. Der Wagebalken balancirte durch beiläufig 3 Minuten, als der
Bruch eintrat. Ein Assistent saß im Augenblicke des Bruches 15 bis 20 Fuß (4,5 bis
6m) von dem Apparate entfernt; es
hatte, nachdem die letzte Adjustirung des Gewichtes vorgenommen war, Niemand die
Wage berührt.
Dies ist ein Fall, welcher in der Erfahrung des Verfassers seines Gleichen nicht hat.
Er beweist die Möglichkeit einer Verminderung der Widerstandskraft, auf die man
Rücksicht nehmen muß, sobald sich die Inanspruchnahme eines zur
„Zinn-Klasse“ gehörigen Metalles der Bruchgrenze
nähert. Das Spannungsdiagramm dieses Probestückes schmiegt sich so ziemlich einer
Hyperbel an, das Gesetz Hooke's
„ut tensio sic vis“ bewährt sich,
wie gewöhnlich, bis zu dem Punkte als gut, bei welchem die Belastung etwa die Hälfte
der maximalen ist.
In folgender Tabelle III sind die nähern Daten des Versuches eingetragen.
III. Probestück Nr. 599: 90 Th. Zink, 10 Th. Kupfer = 1 ×
0,992 × 22 Zoll (25,4 × 25,2 × 558mm,8).
Textabbildung Bd. 223, S. 340
Das Probestück wurde unter Spannung belassen um 11 Uhr 22 Min. Vormittag und die
Abnahme des Widerstandes in folgenden Zeitintervallen gemessen:
k
k
11
Uhr
37
Min.
1133
Pfd.
= 513,93
12
Uhr
39 1/2
Min.
10,23
Pfd.
= 464,03
11
„
50
„
1093
„
= 495,78
12
„
53 1/2
„
1003
„
= 454,96
12
„
2
„
1070
„
= 485,35
12
„
58 1/2
„
993
„
= 450,42
12
„
8
„
1063
„
= 482,18
1
„
20
„
911
„
= 413,23
12
„
25
„
1043
„
= 473,10
Um 1 Uhr 23 Min. Nachmittag brach das Probestück.
Ein Beispiel ähnlichen Verhaltens wird von dem vollständig anders beschaffenen
Probestück Nr. 596 geliefert und ist auf der Tafel B im Diagramm und in der Tabelle IV (S. 341)
in den Beobachtungswerthen dargestellt. Obwohl dieses Probestück hart, spröde und
elastisch war, so muß es doch noch nach seinem Verhalten sowohl bei continuirlicher,
als auch bei absatzweise wirkender Belastung der Zinn-Klasse zugerechnet
werden. Der Verfasser muß annehmen, daß ein Unterschied besteht zwischen dem
„Flusse“, wie er an diesen Metallen zu beobachten ist, und
jenem „Flusse“, welcher nach seiner frühern Abhandlung die
Aufhebung innerer Spannungen und dadurch bedingt eine Erhöhung der
Elasticitätsgrenze bei dauernder Belastung hervorbringt. Diese letztere Erscheinung
–
IV. Probestück Nr. 596: 75 Th. Zink, 25 Th. Kupfer.
Zweiter Guß 0,985 × 0,985 × 0,985 × 22 Zoll
(24,92 × 24,92 × 558mm,8).
Textabbildung Bd. 223, S. 341
die Erhöhung der Elasticitätsgrenze durch Spannung –
wurde vom Verfasser in sehr schlagender Weise bei Gelegenheit der Biegung von
Eisenstäben durch transversalen Zug beobachtet. Die Tafel
B zeigt die durch transversales Biegen
erhaltenen Spannungsdiagramme von vier Probestücken Nr. 648 bis 651, welche aus
derselben Stange gewöhnlichen Schmiedeisens (Schweißeisens) hergestellt waren. Von
diesen vier Stücken wurden die zwei erstern in der oben genannten Fairbank'schen
Maschine geprüft, bei welcher die „Zeitversuche“ so angestellt
werden können, daß sich die Last selbstthätig in dem Sinne ändert, um die Durchbiegung constant zu
erhalten. Die beiden letzten Probestücke wurden mit directer Belastung geprüft, so
daß die Last constant blieb und die Durchbiegung sich änderte. Die zwei erwähnten Paare von Probestücken wurden
zum Bruche gebracht, eines von jedem Paare durch fortwährende Zugabe von Gewichten,
wobei keine Zeit zur Erhöhung der Elasticitätsgrenze durch Spannung gelassen wurde.
Das andere Stück in jedem Paare wurde absatzweise belastet und die Erhöhung der
Elasticitätsgrenze sowie die Setzung gemessen. Die Erhöhung der Elasticitätsgrenze
durch längere Einwirkung äußerer Kräfte ist nun schon eclatant erwiesen für das
Eisen und die zur selben Klasse gehörigen Metalle bei Ausdehnung, Torsion,
Zusammendrückung und Biegung, und es müssen nach Ansicht des Verfassers die
langbekannten Effecte des Kalthämmerns, des Kaltrollens und Drahtziehens in ihrer
verstärkenden
V bis VIII. Probestücke aus Schmiedeisen Nr. 648 bis 651 unter
transversaler Belastung:1 × 1 × 28 Zoll (25,4 × 25,4
× 711mm,2). 22 Zoll (553mm,8) zwischen den
Unterstützungspunkten.
V. Nr. 648 in Fairbank's Maschine geprüft.
Textabbildung Bd. 223, S. 342
Textabbildung Bd. 223, S. 343
* Die Spannung wurde allmälig auf 3 Pfd. (1*k,36) reducirt und
eine Anzahl von Ablesungen gemacht, dann allmälig auf 2238 Pfd. (1015*k,16) erhöht
und die Ablesungen entsprechend den früheren genommen, wobei gefunden wurde, daß das
Wachsen der Durchbiegung proportional zum Wachsen der Belastung war.
Textabbildung Bd. 223, S. 344
und härtenden Wirkung ebensosehr durch diese moleculare
Veränderung als durch das einfache Verdichten und Schließen von Höhlungen und Poren
erklärt werden.
Aus den Diagrammen der Tafel B treten die durch transversale Biegung entstehenden Erscheinungen
noch vollständiger und deutlicher hervor als aus den Tabellen V bis VIII (S. 342 bis
346). Ein Studium dieser typischen Beispiele kann nicht verfehlen, sowohl
interessant als auch instructiv zu sein.
Bezugnehmend auf die Diagramme der Tafel B (Eisengruppe Nr. 648 bis 651),
Zinn-Gruppe Nr. 556 und 599) weisen beide Gruppen, wenn durch Biegung
beansprucht, ein allmälig abnehmendes Bestreben auf, ihre ursprüngliche Form
wiederherzustellen. Bei der Zinn-Gruppe scheint dieser Verlust am
Wiederherstellungsvermögen unbestimmt zu verlaufen, und, wie aus einem der hier
angeführten Beispiele ersichtlich, selbst bis zum Bruche sich fortzusetzen. Bei
Eisen und der Gruppe von Metallen,
VI. Nr. 649 in Fairbank's Maschine geprüft.
Belastung.
Durchbiegung.
Belastung.
Durchbiegung.
Pfd.
k
Zoll.
mm
Pfd.
k
Zoll.
mm
103
46,72
0,0139
0,353
1462
663,16
0,1505
3,823
200
90,72
0,0238
0,604
1480
671,33
0,1569
3,985
300
136,08
0,0328
0,833
1500
680,40
0,1619
4,112
405
183,71
0,0425
1,079
1520
689,47
0,1709
4,341
500
226,80
0,0519
1,318
1540
698,54
0,1804
4,582
600
272,16
0,0602
1,529
1560
707,62
0,2078
5,278
700
317,52
0,0689
1,750
1580
716,69
0,2429
6,170
800
362,88
0,0787
1,999
1600 a
725,76
0,2854
7,249
900
408,24
0,0889
2,258
Nach 2 3/4 M
0,3629
9,218
1000
453,60
0,0982
2,494
1620
734,83
0,3704
9,408
1100
498,96
0,1081
2,746
1640
743,90
0,3831
9,731
1200
544,32
0,1171
2,974
Nach 6 M
0,4404
11,186
1300
589,68
0,1279
3,249
1660
752,98
0,4479
11,377
1400
635,04
0,1398
3,551
1680 b
762,05
0,4599
11,681
1420
644,11
0,1435
3,645
–
–
–
–
1442
654,09
0,1472
3,739
2350
1065,96
5,5770
141,656
161,733
a Bei 1600 Pfd. (725k,76) sank der Hebel momentan, die Pressionsschraube wurde niederwärts
bewegt, um den Wagebalken 2 3/4 Min. lang in Balance zu erhalten, wobei sich die
Durchbiegung auf 0,3629 Zoll (9mm,218)
vergrößerte.
b Bei 1680 Pfd. (762k,05) wurde die Pressionsschraube abermals niederwärts bewegt und das
Gewicht am Wagebalken verschoben, um ihn in Balance zu erhalten. Der Wagebalken
vibrirte auf und nieder – augenblicklich fallend oder steigend, wenn das
Handrad langsamer oder schneller gedreht wurde.
VII. Nr. 650 bei directer Belastung geprüft.
Belastung.
Durchbiegung.
Belastung.
Durchbiegung.
Pfd.
k
Zoll.
mm
Pfd.
k
Zoll.
mm
100
45,36
0,0150
0,381
800
362,88
0,0858
2,179
200
90,72
0,0239
0,607
1200
544,32
0,1456
3,698
400
181,44
0,0425
1,079
1400
635,04
0,1749
4,442
600
272,16
0,0638
1,620
1500 c
680,40
0,2143
5,443
c Bei 1626 Pfd. (737k,55) wurde keine Ablesung gemacht. Gewichte wurden, wie folgt, schnell
nach einander zugegeben und zwar 4 bis 5 Stück in jeder Minute: 82, 25, 42, 15, 16,
10, 15,5, 16, 25, 25, 25, 13, 11,5, 16, 27, 62, 40,5, 61, 45, 62, zusammen 2260,5
Pfd. (1025k,36). Das Probestück senkte sich
rasch; sein Seitenzug spaltete das Holzfutter der Böcke, in welchen es eingespannt
war. Die bleibende Setzung nach Entfernung der Last betrug 2,5 Zoll (63mm,5.) Die totale Biegung berechnet sich,
wie folgt: Nachdem die Elasticität des Stückes dieselbe blieb, so ist die Größe der
Abbiegung über den Betrag der Setzung hinaus der Belastung direct proportional.
(Dies ist erwiesen durch den Parallelismus der elastischen Linien mit der
ursprünglichen Linie innerhalb der Elasticitätsgrenze.) So war bei 800 Pfd. (362k,88) die bleibende Setzung kaum
wahrnehmbar, die Durchbiegung 0,0858 Zoll (2mm 179), daher 800 : 0,058 = 2260 : 0,242. Demnach ist 0,242 (aus der
Proportion berechnet) + 2,5 (gemessene bleibende Setzung) = 2 742 Zoll (69mm
,65) die factische Durchbiegung.
VIII. Nr. 651 bei directer Belastung geprüft.
Belastung.
Durchbiegung.
Belastung.
Durchbiegung.
Pfd.
k
Zoll.
mm
Pfd.
k
Zoll.
mm
100
45,36
0,0158
0,401
Nach 48 St 30 M
1,9245
48,882
200
90,72
0,0275
0,698
2222
1007,90
1,9379
49,223
400
181,44
0,0489
1,242
2288
1037,84
2,1386
54,320
600
272,16
0,0709
1,801
Nach 12 M
2,9535
75,019
803
364,24
0,0913
2,318
2266
1027,86
2,9928
76,017
1000
453,60
0,1141
2,898
Nach 17 M
3,0157
76,599
1200
544,32
0,1394
3,541
Nach 3 St 37 M
3,0236
76,797
1400
635,04
0,1701
4,321
2288
1037,84
3,0290
76,937
1500
680,40
0,2465
6,261
2350
1065,96
3,0426
77,282
Nach 8 M
0,4307
10,940
2370
1075,03
3,0433
77,300
1600
725,76
0,4890
12,421
Nach 25 St 15
M
3,0677
77,920
Nach 6 M
0,6504
16,521
2422
1098,62
3,0701
77,981
Nach 5 St 46 M
0,6598
16,759
2452
1112,23
3,0732
78,059
1700
771,12
0,6700
17,018
2484
1126,74
3,0812
78,262
Nach 3 M
0,6716
17,059
Nach 39 St 40 M
4,2591
108,181
Nach 16 St
0,7615
19,342
Nach 43 St 20 M
4,2591
108,181
1800
816,48
0,7710
19,583
2513
1139,90
4,2623
108,262
1900
861,84
1,0904
27,696
2556
1159,40
4,2670
108,382
Nach 3 St 15 M
1,8567
47,140
Nach 4 St 20 M
4,2749
108,582
Nach 45 St 45 M
1,8709
47,521
2589
1174,37
4,2749
108,582
2005
909,47
1,8787
47,719
Nach 48 St
4,6591
118,341
Nach 3 St
1,8819
47,800
Nach 61 St 30 M
4,6701
118,621
2052
930,79
1,8886
47,970
Die Gewichte erreichten den Boden
2115
959,36
1,8921
48,059
und der Versuch wurde beendigt.
für welche ersteres als Typus angenommen wurde, wird die
Abnahme an Wiederherstellungsvermögen allmälig weniger und weniger rapid, erreicht
endlich eine Grenze, nach Erreichung welcher sich das Metall gestärkt erweist und
die Elasticitätsgrenze erhöht gefunden wird. In dieser Hinsicht werden die zwei
Metallgruppen in grade entgegengesetzter Weise durch die Zeitdauer des Zuges
beansprucht.
Die Diagramme zeigen besser als die tabellarischen Zusammenstellungen, daß die
intermittirend beanspruchten Probestücke sowohl eine Erhöhung der
Elasticitätsgrenze, als der Bruchfestigkeit erfahren. Der Parallelismus der
„elastischen Linien“, welche durch die zeitweisen
Entlastungen erhalten wurden, zeigt, daß der Elasticitätsmodulus durch die Erhöhung
der Elasticitätsgrenze nicht alterirt wird.
Die Evidenz des intermolecularen Flusses wurde in einer sich den Sinnen direct
kundgebenden Weise vorgeführt und zwar mit den an der Zinn-Gruppe
vorgenommenen Experimenten. Wenn eine Zinnstange gebogen wird, so ist das als
„Zinnschrei“ bekannte Geräusch wahrnehmbar. Dieses Geräusch
wurde, soweit es dem Verfasser bekannt ist, bisher nie wahrgenommen, wenn eine
Stange gebogen und hierauf vollkommen ruhig gehalten wurde. In einigen kürzlich vorgekommenen.
Fällen, beim Experimentiren auf Biegung mit den Metallen der zweiten Gruppe, zeigte
sich, daß Probestücke, welche bei constanter Durchbiegung erhalten wurden, dieses
Geräusch stundenlang wahrnehmen ließen, indem sie allmälig bleibende Setzung
annahmen und die Wiederherstellungskraft verloren. Während der Vornahme einiger
Experimente ereignete sich ein sehr markanter Fall von Verminderung der bleibenden Setzung bei länger dauernder Entlastung,
welcher von Prof. W. A. Norton beobachtet und beschrieben
wurde. Die Wiederherstellung an geraderichtender Kraft des gebogenen Probestückes
war manchmal in beträchtlichem Maße wahrzunehmen; sie belief sich auf nahe 30 Pfd.
(13k,61) in 15 Minuten. Die
Aufzeichnungen der Versuche sind in folgender Tabelle IX enthalten.
IX. Probestück Nr. 563 : 17,5 Th. Kupfer, 82,5 Th. Zinn.
0,986 × 0,993 × 22 Zoll (25,04 × 25,22
× 558mm,8).
Belastung.
Durchbiegung.
BleibendeSetzung.
Belastung.
Durchbiegung
BleibendeSetzung.
Pfd.
k
Zoll.
mm
Zoll.
mm
Pfd.
k
Zoll.
mm
Zoll
mm
10
4,54
0,0027
0,069
–
–
200
90,72
0,1798
4,567
–
–
20
9,07
0,0070
0,178
–
–
240
108,86
0,2503
6,358
–
–
40
18,14
0,0153
0,389
–
–
280
127,01
0,3762
9,555
–
–
60
27,22
0,0256
0,650
–
–
300
136,08
0,4597
11,676
–
–
80
36,29
0,0365
0,927
–
–
5
2,27
–
–
0,3084
7,833
100
45,36
0,0499
1,267
–
–
Bleibende Setzung fiel in
5
2,27
–
–
0,0092
0,234
–
–
2 St 20 M auf.
0,2845
7,226
140
63,50
0,0804
2,042
–
300
136,08
0,5332
13,543
–
–
180
81,66
0,1343
3,411
–
–
310
140,62
Probestück brach während des
200
90,72
0,1666
4,232
–
–
Aufsetzens von Gewichten.
5
2,27
–
–
0,0821
2,085
Nachdem das Probestück mit 300 Pfd. (136k,08) belastet und die Ablesung gemacht war, wurde die Schraube so weit
zurückbewegt, daß der Wagebalken bei 5 Pfd. (2k,27) balancirte. Der Pressionsblock der Schraube berührte das Probestück
hierbei kaum merklich. Die Setzung wurde, wie in der Tabelle IX verzeichnet, im
Betrage von 0,3084 Zoll (7mm,83) abgelesen,
worauf sich der Wagebalken langsam zu erheben begann. Nachher wurde die
Pressionsschraube abermals zurückbewegt, so daß der Wagebalken wieder bei 5 Pfd.
(2k,27) balancirte, und die Setzung in
der Größe von 0,3022 Zoll (7mm,68)
gemessen; die Zeit hierbei war 2 Minuten. Der Wagebalken erhob sich nun bei constant bleibender Setzung von Neuem, das Gewicht an ihm
wurde weiter hinausgeschoben und er selbst bei 10 Pfd. (4k,54) balancirt, wobei die Zeit wieder 2
Minuten betrug. Nach weitern 2 Minuten balancirte der Balken bei 14 Pfd. (6k,35). Die Pressionsschraube wurde wieder
so weit rückwärts bewegt, bis der Wagebalken bei 5 Pfd. (2k,27) balancirte, wobei die abgemessene
Setzung nunmehr 0,2998 Zoll (7mm,89)
betrug. Der Wageballen begann sich wieder zu erheben. Nach 2 Minuten balancirte er
bei 10 Pfd. (4k,54), nach 10 Minuten bei 16
Pfd. (7k,26) und nach 29 Minuten bei 23
Pfd. (10k,43). Der Balken wurde neuerdings
bei 5 Pfd. (2k,27) zum Balanciren gebracht,
die Setzung betrug nun 0,2902 Zoll (7k,37).
Der Wagebalken erhob sich nach 4 Minuten; nach 29 Minuten balancirte er bei 14 Pfd.
(6k,35) und in 65 Minuten darauf bei 20
Pfd. (9k,07). Der Balken wurde abermals bei
5 Pfd. (2k,27) zum Balanciren gebracht,
wobei die Setzung sich auf 0,2845 Zoll (7mm,23) belief. Die ganze Abnahme der Setzung während 2 Stunden 20 Minuten
betrug 0,3084 – 0,2845 = 0,0239 Zoll (0mm,61). Sodann wurden die 300 Pfd. (136k,08) wieder aufgesetzt wobei die Biegung mit 0,5332 Zoll (13mm,54) abgelesen wurde. Die Belastung wurde
weiter vergrößert; ehe sie jedoch 310 Pfd. (140k,6) erreicht hatte, brach der Probestab.
Tafeln