| Titel: | Ueber Gujer's neuen Ellipsographen; von G. Delabar. |
| Autor: | G. Delabar |
| Fundstelle: | Band 223, Jahrgang 1877, S. 461 |
| Download: | XML |
Ueber Gujer's neuen Ellipsographen; von G. Delabar.
Mit Abbildungen auf Taf.
XII [a. c/1].
Delabar, über Gujer's Ellipsograph.
Die Ellipse ist bekanntlich diejenige Curve, die neben dem Kreis und der geraden
Linie bei unsern graphischen Arbeiten am meisten vorkommt und auch in den Künsten
und Gewerben vielfältige Anwendung findet. Deshalb wurde denn auch schon oft
versucht, einen Ellipsographen, d.h. ein Instrument zu construiren, mit dem man die
Ellipse wie die Kreislinie mit dem Zirkel beschreiben könne. Dieses Problem
bezüglich der Construction eines vollkommenen, allen Anforderungen entsprechenden
Ellipsographen ist aber bis jetzt, so viele und verschiedenartige Lösungen auch
schon versucht worden sind, noch immer ungelöst und ein frommer Wunsch
geblieben.
Im Hinblick auf diese Thatsache verdient jede neue Construction, welche die erwähnte
Aufgabe in irgend einer Weise besser als die vorausgehenden Instrumente zu lösen
versucht, öffentlich bekannt zu werden. Bevor ich jedoch den neuen Ellipsographen,
der zu diesem Artikel den Anlaß gegeben, näher beschreiben und darstellen werde,
erlaube ich mir, auf eine Abhandlung von T. Rittershaus
in den Verhandlungen des Vereins zur Beförderung des Gewerbfleißes, 1874 Heft 3,
hinzuweisen, in welcher so ziemlich alle bis zu jener Zeit bekannt gewordenen
Constructionen von Ellipsographen zusammengestellt und vom allgemeinen Standpunkt
der Kinematik aus kritisch besprochen worden sind. Hiernach beruhen die meisten,
nämlich 9/10 sämmtlicher Ellipsographen, auf dem Problem der Cardanischen
KreiseWenn ein Kreis innerhalb eines andern rollt, so beschreiben seine sämmtlichen
Umfangspunkte Hypocycloiden, und sämmtliche übrigen Punkte seiner mit ihm
fest verbunden gedachten Ebene, sofern sie innerhalb seines Umfangs liegen,
verkürzte, sofern sie außerhalb desselben liegen, verlängerte Hypocycloiden.
Ist der Durchmesser des rollenden Kreises gleich dem Radius des ruhenden, so
gehen sämmtliche Curven in Ellipsen über und speciell diejenigen der
Umfangspunkte in Ellipsen mit der kleinen Achse Null und der großen Achse
gleich dem Durchmesser des ruhenden Kreises. Diesen längst bekannten Satz,
auf den, wie es scheint, der bekannte Mathematiker Cardano zuerst aufmerksam gemacht hat, wird nach dem Vorgange von
Reuleaux in seinen kinematischen
Mittheilungen (Verhandlungen zur Beförderung des Gewerbfleißes, 1872 S. 174)
das „Problem der Cardanischen Kreise“ genannt., wenn dieselben auch, wie gesagt, auf sehr verschiedene Art zur Ausführung
gebracht worden sind.
In dieser Beziehung können dieselben in folgende drei Klassen eingetheilt werden,
nämlich:
1) in Ellipsographen, wobei zwei bewegliche Punkte auf zwei sich
gewöhnlich rechtwinklig schneidenden festen Geraden geführt und die Ellipsen durch einen
dritten Punkt der bewegten Ebene beschrieben werden;
2) in Ellipsographen, wobei ein Punkt auf einer Geraden und ein
zweiter Punkt auf einem Kreis geführt und die Ellipse durch irgend einen dritten
Punkt der bewegten Ebene beschrieben wird;
3) in Ellipsographen, wobei ein Kreis in einem doppelt so großen
Kreis rotirt und die Ellipse von irgend einem Punkt des rollenden Kreises
erzeugt wird.
Zu einer 4. Klasse von Ellipsographen kann man alle diejenigen zählen, die so
eingerichtet sind, daß die Ellipse in ihrer Eigenschaft als Kegelschnitt beschrieben
wird und die deshalb auch „Conographen“ heißen.
Die älteste Construction von allen diesen verschiedenen
Ellipsographen ist jene mit der bekannten Kreuzführung, wie sie zuerst von Bion
Traité de la construction et des principaux
usages des instruments mathématiques. Nouvelle Edition. La
Haye 1723. beschrieben worden ist und im Grunde nur als eine Umkehrung des alten von
Leonardo da Vinci angegebenen Ovalwerkes zu betrachten
ist, welches dieser geniale Künstler zum Abdrehen elliptischer Arbeitsstücke in
Vorschlag gebracht hatte, und von den nachfolgenden Maschinenbauern wirklich, wenn
auch nicht immer in der vollkommensten Form, zur Anwendung gekommen ist.Reuleaux, Verhandlungen zur Beförderung des
Gewerbfleißes, 1873 S. 99 und 114.
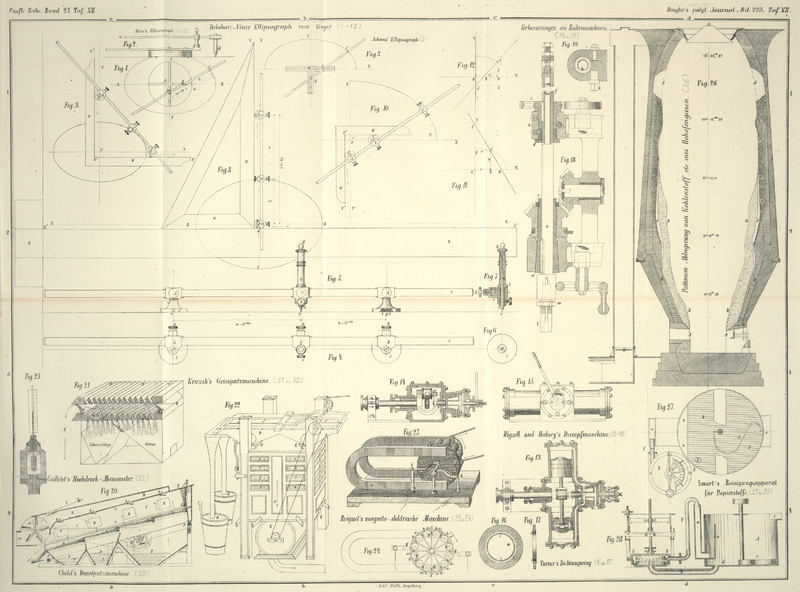
Bei diesem Ellipsographen, den wir in Fig. 1 und 2 [a/1] (nach einem der Kantonschule in St. Gallen angehörenden Modell)
mitabgebildet haben, gleiten in den sich rechtwinklig kreuzenden Führungsnuthen zwei
entsprechende schwalbenschwanzförmige Zapfen – prismatische Klötzchen, sogen.
Federn – die mittels Schrauben an der Stange, welche zugleich auch das
Stäbchen mit dem Zeichenstift trägt, befestigt sind. Je nach der Entfernung der
beiden geführten Punkte A, B unter sich und vom
beschreibenden Punkt C richtet sich die Größe und
Gestalt der zu beschreibenden Ellipsen. Die Entfernungen der Führungspunkte vom
beschreibenden Punkt sind bei dieser Einrichtung bekanntlich immer gleich den beiden
Halbachsen, nämlich AC = a und BC = b, und die Entfernung AB unter sich selbst
ist gleich der Differenz (a – b) derselben. Bei dieser allerdings sehr einfachen
Construction bildet jedoch der Kreuzungspunkt O der
beiden Führungsnuthen den schwachen Punkt; denn sind die in den Ruthen sich
verschiebenden Prismenzapfen zu lang, so hindern sie sich selbst bei der Bewegung;
macht man sie aber zu kurz, so wird die Führung unsicher, wenn ein Zapfen den Kreuzungspunkt
passirt, und in beiden Fällen fällt in Folge dessen die beschriebene Ellipse
natürlich unegal aus. Zudem liegt in der angewendeten Form des Führungskörpers, bei
welcher die Führungsnuthen mit der Stange des Zeichenstiftes auf der obern Fläche desselben angebracht sind, selbst ein
Hinderniß, auch solche Ellipsen beschreiben zu können, deren kleine Achse kleiner als die Arme des Führungskreuzes ist.
Beiden Uebelständen suchte im J. 1748 Adams
Geometrical and geographical Essays containing a
great description of the mathematical Instruments etc. 4. Edition. London 1813. dadurch abzuhelfen, daß er das Kreuzstück auf die T-Form reducirte und sich hierbei darauf beschränkte, statt der
vollen Ellipse je nur eine Hälfte derselben in einem zusammenhängenden Zuge zu
beschreiben, welche beide Hälften in ihrer Vereinigung dann erst die ganze Ellipse
ausmachen. Bei dieser Construction, die in Figur 3 skizzirt ist, gibt
es daher keinen Kreuzungspunkt, und der eine, im Querarm geführte Punkt A kommt in seinen beiden Endlagen allerdings bis zum
Vereinigungspunkt O der drei Arme, aber aus dem Querarm
kommt er nicht heraus. Mit diesem so modificirten Ellipsographen lassen sich alle
Ellipsen beschreiben, deren Halbachsendifferenz nicht größer als der kleinste Arm
der T-Form und deren kleine Halbachse nicht
besonders groß ist, die also mehr eine längliche Gestalt haben. Unsicher wird aber
mit demselben die Zeichnung solcher Ellipsen, deren Halbachsendifferenz sehr gering
ist, welche daher eine mehr runde, dem Kreis ähnliche Gestalt erhalten sollen.
Wird aber bei dieser so abgeänderten Construction die Stange mit dem Zeichenstift
entsprechend dem oben angeführten Ovalwerk von Leonardo da
Vinci unter dem T-förmigen Führungsstück
angebracht, so kann man den Zeichnungsstift auch zwischen den geführten Punkten
anbringen und somit Ellipsen beschreiben, für welche nicht mehr die Differenz,
sondern die Summe der Halbachsen durch deren Entfernungen vom beschreibenden Punkt
bestimmt ist, und die daher jede beliebige, dem Kreis ähnliche Form annehmen und
selbst in diesen übergehen können. Allein die praktische Ausführung dieser
Abänderung hatte wieder andere Uebelstände im Gefolge, und so war es denn auch mit
allen spätern Ellipsographen-Constructionen, unter denen mehrere, wie
namentlich jene von Farey
Transactions of the Society for the encouragement of
manufactures and arts, 1812 Bd. 35 S. 118., Cubitt
Transactions, Bd. 34 S. 131., Webb (1845 97
22)London Mechanics' Magazine, 1845 Bd. 42 S.
82., Göhl
Bayerisches Kunst- und Gewerbeblatt, 1861 S. 17. und Clements
Transactions, Bd. 36 S. 133. (die alle der
oben angedeuteten 1. Klasse angehören), jene von Eichberg
Polytechnisches Centralblatt, 1852 S. 669. und Bowly
Scientific American, 1868 Bd. 19 S. 8. (die zur 2. Klasse gehören), jene von Saladin
Bulletin de Mulhouse, 1847 Bd. 47 S. 190., Henry
Annales des ponts et chaussées, 1872 série 5, t. 3
p. 459., Hamann und Hempel
Brevets d'invention, 1845 t. 35. p. 231. und Thomas (* 1867 184
237)Bulletin d'encouragement, November 1866 S.
648. (der 3. Klasse zugehörig) und jene von Meyn
Civilingenieur, 1862 Bd. 8 S. 247. und Drzewiecki
Wochenschrift des n.-ö. Gewerbvereins, 1873., (der 4. Klasse angehörend) als sehr hübsche und ingeniöse Erfindungen
bezeichnet werden müssen, von denen aber gleichwohl noch keine in allgemeine
Aufnahme gekommen ist. Mit der vom Erfinder jeweilen angestrebten Veränderung oder
Verbesserung wurde das Instrument meistens auch complicirter und für den Gebrauch
schwieriger zu handhaben. Zudem ist noch bei keinem dieser Instrumente das
wichtigste und schwierigste Problem für jeden Ellipsographen, die Reißfeder beim Zeichnen stets tangential an den Ellipsenbogen und zugleich normal zu der Papierfläche
desselben einzustellen, in erwünschter Weise gelöst worden, obschon
dasselbe schon oft zu lösen versucht und auch schon auf die voraussichtlich
leichteste Lösung hingewiesen worden ist.Vgl. Rittershaus a. a. O. S. 391. Dieser
Abhandlung sind auch vorstehende Citate entnommen.
Auch der neue Ellipsograph, den ich nun im Folgendem unter Zugrundelegung der
Abbildungen Fig.
4 bis 10 beschreiben werde, macht in dieser Beziehung keinen Anspruch auf eine
vollkommene und allen Anforderungen entsprechende Lösung. Er ist darum auch nicht
zum Zeichnen der Ellipsen mit Reißfeder in Tusch, sondern nur zum Vorzeichnen
derselben mit dem Bleistift bestimmt. Für diese freilich ganz bescheidene Aufgabe
empfiehlt er sich aber sowohl durch seine zweckmäßige und höchst einfache
Einrichtung, als auch durch seine leichte und praktische Handhabung ganz
ausgezeichnet. Derselbe ist von Ingenieur Gujer (z. Z. im
Hause von Rieter und Comp.) in
Winterthur erfunden und wird vom Mechaniker Hommel-Esser in Aarau (bekannt durch
seine ausgezeichnet gearbeiteten mathematischen Zeichnungsinstrumente) sowohl in
Neusilber als in Messing in verschiedener Größe ausgeführt.Bei einer Länge des Stabes von 25cm
und für Ellipsen von 5 bis 86cm
totaler Achsenlängen kostet ein solcher Ellipsograph in Neusilber 24
Franken, in Messing 22,60 Franken.
Das Instrument selbst besteht, wie man aus den Figuren 4 bis 7
ersieht, in welchen es
in wahrer Größe im Grundriß, Aufriß und theilweise im Durchschnitt abgebildet ist,
aus einem prismatischen Stab S von quadratischem
Querschnitt mit drei verschiebbaren Hülsen A, B und C, von denen die mittlere C
die Bleistiftfassung G sammt Bleistift γ trägt (der unten möglichst genau centrisch
gespitzt sein soll) und die beiden äußern A und B unten mit elfenbeinernen Rollfüßen J versehen sind und sämmtlich mittels Klemmschrauben K an den Stab S so befestigt
werden, daß ihre Mitte von der Mitte der Bleistifthülse C genau die halben Achsenlängen a und b repräsentiren.
Zum genauen Einstellen der Hülsen dienen die an den Grundflächen der Rollen bei der
Umkehrung des Instrumentes sichtbaren zugespitzten, aber etwas zurückstehenden
Stahlachsen α und β (Fig. 5 und 6) und ein abgeschrägter
Millimeter-Maßstab, womit man die Entfernungen des Centrums (α und β) einer
jeden Achse bis zur Bleistiftspitze γ mißt. Dabei
wird der Bleistift, der genau 2mm dick ist,
oder dafür ein eben so starker Stahlstift, so weit in die Fassung (Fig. 7) eingesetzt und mit
der Schraube k festgeklemmt, daß er mit der Spitze das
Papier kaum berührt.
Sind die drei Hülsen auf die verlangten oder vorgeschriebenen Entfernungen, zum
Beispiel für a = 9cm und b = 6cm, wie in Fig. 4 und 5, richtig eingestellt und
mit den betreffenden Schrauben auf den Stab festgeklemmt, so wechselt man den
Stahlstift mit dem Bleistift wieder aus und klemmt ihn ebenso mit der Schraube k in die Bleistiftfassung G
der Hülse C leicht ein. Das Instrument ist dann zum
Zeichnen der betreffenden Ellipse vorbereitet. Dazu bedarf man nun noch einer
Reißschiene R, und eines Winkels W, und nachdem man zur größern Sicherheit vorher noch die beiden
Achsenlagen OX und OY, sowie die ihnen parallelen Aequidistanten O
'X
' und O
'Y
' als Tangenten an die Rollenumfänge (deren Radius genau 1cm beträgt) auf dem Papier vermerkt hat,
werden vor Allem Reißschiene und Winkel sammt Instrument in Bezug auf die
vorgezeichneten Ellipsenachsen eingestellt, wie in Figur 8 für das rechte
obere Viertel der Ellipse zu sehen ist. Dabei wird zuerst die Reißschiene vorwärts
geschoben, bis ihre obere (hintere) Kante mit der entsprechenden Parallelen O
'X
' zusammentrifft und die an derselben anliegende Rolle J mit ihrem Achsenstift β genau auf der
einen, hier der ersten Ellipsenachse OX steht;
alsdann wird die Schiene festgehalten und der Winkel gegen die Rollen nachgerückt,
bis seine Kante (zur Rechten) mit der entsprechenden Parallelen O
'Y
' zusammentrifft und die Rollenumfänge J, J genau
berührt, die Bleistiftspitze γ und die Spitzen
α und β
der Rollenachsen also auf der andern, hier der zweiten Ellipsenachse OY
genau centrisch
eingestellt sind. Nun hält man zugleich mit der linken Hand, welche die Schiene
hält, auch den Winkel fest und bewegt mit der andern Hand das Instrument längs der
Schiene und dem Winkel, wie durch Pfeile angedeutet ist, d.h. so, daß die eine Rolle
B stets an der Schiene R
und die andere A am Winkel W
genau anliegt und erstere zugleich in der Richtung von O' gegen X' und die andere von Y' gegen O' sich rollend
fortbewegt.
Ist die Bewegung so weit fortgeschritten, daß die Rolle A
an die Stelle der Rolle B gekommen ist und nun sowohl
die Schiene als den Winkel berührt, so hat inzwischen der Bleistift γ, der nach dem Einstellen rasch gelüftet
(losgeschraubt) und von der darüber befindlichen schwachen Spiralfeder mittels des
Kopfes des eingesetzten Bolzens an die Papierfläche angedrückt wird (wie sich am
besten aus der Durchschnittszeichnung in Fig. 7 ergibt), genau ein
Viertel der Ellipse und zwar den Bogen CD
beschrieben. Ohne die Schiene zu verrücken, legt man nun den Winkel auf die andere,
rechte Seite und stellt denselben mit dem Instrument genau wie vorher ein und zieht
auf gleiche Weise das zweite Viertel CE der
Ellipse, und indem man hierauf die Schiene weiter hinaufschiebt, den Winkel auf der
untern Seite einmal rechts und einmal links ansetzt und das Instrument gegen beide,
wie oben, richtig einstellt, erhält man nach einander auch die beiden andern Viertel
EF und FD
und damit die ganze Ellipse.
Kann man die Schiene und den Winkel durch Jemanden halten lassen oder mit Gewicht
beschweren, so erleichtert dies das Arbeiten; nöthig ist es aber schon darum nicht,
weil, wie Referent aus seinen Arbeiten mit dem Instrumente gefunden, die Reißschiene
überhaupt weggelassen werden kann, und ein offener Winkel, wie ihn die Steinmetze
und Zimmerleute gebrauchen, vollkommen genügt. Das Verfahren mit einem solchen
Winkel ist in Figur
9 noch besonders angedeutet. Dasselbe wird auf diese Weise, wie man aus
Erfahrung bald selbst finden wird, sogar noch bedeutend vereinfacht und erleichtert,
wie auch das Einstellen und Zeichnen mit dem neuen Instrument auf diese wie auf die
erste Art überhaupt bald erlernt ist und das Zusammensetzen der ganzen Ellipse aus
den vier Vierteln nach einiger Uebung leichter und schneller geht, als man zum
Voraus glaubt. Dasselbe darf daher für den angegebenen Gebrauch allen Zeichnern und
Lithographen etc., sowie namentlich auch den Schulen bestens empfohlen werden. Auch
Professor Culmann am Polytechnicum in Zürich, welchem
dasselbe vorgezeigt worden ist, sprach sich über die praktische Ausführung des
Instrumentes und dessen Brauchbarkeit sehr günstig aus. In der That verdient es,
wenn man erwägt, daß die Anwendbarkeit desselben sozusagen keine Grenzen hat, indem mit demselben –
in gehöriger Größe ausgeführt – jede der Gestalt und Größe nach ganz
beliebige Ellipse gezeichnet werden kann, alle Anerkennung.
Von besonderem Interesse ist endlich auch noch die weitere Eigenthümlichkeit des
neuen Instrumentes, daß man nach Belieben, wie in Figur 10, die Hülsen
versetzen, die Bleistifthülse C daher auch an das eine
Ende der Stange bringen und die beiden andern Hülsen A
und B mit den Rollfüßen sich beliebig nähern und auf
diese Weise mit dem Instrument sehr große Ellipsen blos mit Hilfe eines kleinen
Winkels (ohne Schiene) verzeichnen kann.
Zum Beweise endlich, daß das Instrument bei beiden Anwendungen (Fig. 9 und 10) mathematisch richtige
Ellipsen liefert, mögen zum Schlusse noch für beide Fälle die Gleichungen der vom
beschreibenden Punkt C erzeugenden Curven entwickelt
werden. Dazu seien in Fig. 11 und 12 [c/1] OX und OY die beiden zu einander rechtwinkligen
Coordinatenachsen, mit denen auch die Achsenlagen der zu beschreibenden Ellipsen
zusammenfallen, und AB irgend eine Lage der
beweglichen Stange mit den beiden geführten Punkten A
und B und dem beschreibenden Punkt C. Bezeichnet man nun die Abstände AC mit a, BC mit b und die
Coordinaten des beschreibenden Punktes C, nämlich OD mit x und CD mit y, so erhält
man für die Anordnung Figur 11, wenn man CE parallel und gleich DO zieht, aus den ähnlichen Dreiecken ACE und BCD:
b : a =
√(b² – y²) : x
b² : a² = (b² – y²) : x²
b² x² = a² b² – a² y²
a² y² + b² x² = a² b².
für die Anordnung Figur 12, wenn man CD rückwärts verlängert und AE parallel und gleich OD zieht, aus den ähnlichen Dreicken ACE und BCD:
b; a = y
: √(a² – x²)
b² : a² = y² : (a² – x²)
a² y² = a² b² – b² x²
a² y² + b² x² = a² y²,
also in beiden Fällen die bekannte Ellipsengleichung.
Tafeln