| Titel: | Notizen von der Weltausstellung in Philadelphia 1876; von Ingenieur Müller-Melchiors. |
| Fundstelle: | Band 224, Jahrgang 1877, Nr. , S. 19 |
| Download: | XML |
Notizen von der Weltausstellung in Philadelphia 1876; von Ingenieur Müller-Melchiors.
Mit Abbildungen auf Tafel
I.
(Fortsetzung von S. 567 des vorhergehenden
Bandes.)
Müller-Melchiors, Notizen von der Weltausstellung in
Philadelphia 1876.
72. Cosinus-Regulator von
Gebrüder Buß.
(Fig. 1 bis 6 [d/4].)
Schon bei Besprechung der interessanten Regulirungsvorrichtung von J. G. Bodemer (*1876 222 505) 592)
hatten wir auf ein zweites deutsches Ausstellungsobject aus der Klasse der
Regulatoren hingewiesen; es ist dies der Cosinus-Regulator von Gebrüder Buß, Erfinder des bekannten Buß'schen Regulators
(*1871 202 481) *1875 216
195). Beide Constructionen, jede in ihrer Art vortrefflich, sind völlig verschieden
und gradezu entgegengesetzt in ihrer principiellen Begründung, sowie in den damit
angestrebten Zielen.
Während es Bodemer gelungen ist, durch geistreiche
Anordnung des Stellzeuges und Anbringung seiner
Correcturvorrichtung einen Regulator zu schaffen, welcher zum ersten Male in der
Technik eine vollkommene Regulirung erreicht, in Folge dieses Vorzuges und seiner
indirecten Wirkungsweise zur Expansionsregulirung der größten Dampfmaschinen
geeignet und dabei fast unabhängig von der Construction des Geschwindigkeitsmessers ist, besteht der Cosinus-Regulator grade in
einer Verbesserung dieses letztern. Das Resultat dieser Verbesserungen ist zunächst
die Erzielung einer vollständig gleichen Empfindlichkeit
und nahezu constanten Energie des Regulators in allen
Kugelstellungen, ferner aber die Möglichkeit, mittels einer einfachen Vorrichtung
den Regulator aus einem vollständig astatischen in einen mehr oder weniger
statischen umzuändern. Wie wesentlich aber grade dieser Umstand in Betracht kommt,
sobald der Regulator direct und ohne Stellzeug zur Maschinenregulirung benutzt
werden soll, ist in der einleitenden Uebersicht zu Bodemer's Regulator erörtert
worden (Bd. 222 S. 507 und 512). Der Cosinus-Regulator hat somit bei der
ungeheuren Mehrzahl unserer einfachern Dampfmaschinen ein weites Feld seiner
Anwendung, so daß ein näheres Eingehen auf die Begründung seiner Wirkungsweise wohl
am Platze ist.
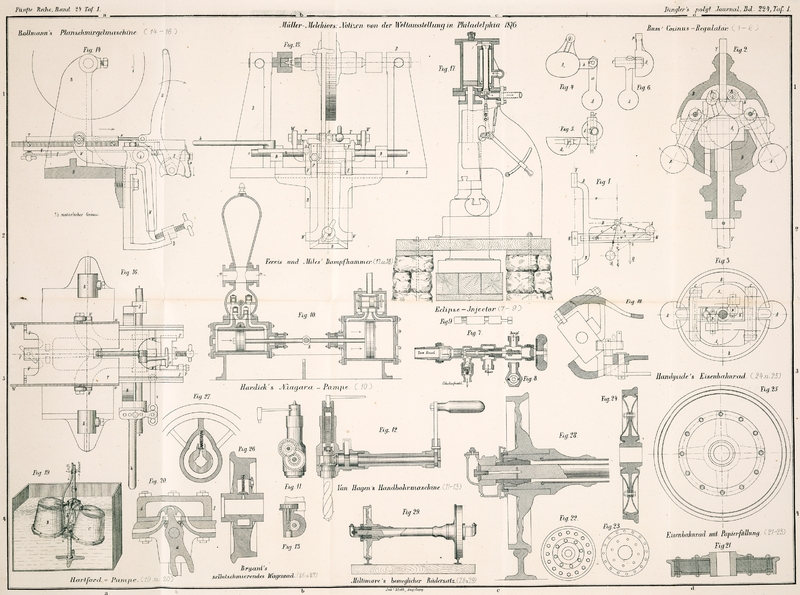
Die Skizze Figur
1 stellt den Cosinus-Regulator in principiellen Linien dar. Y ist die continuirlich rotirende Regulatorspindel, K ein darauf befestigter Arm, B eine gleichfalls mit Y rotirende, aber
auf- und abwärts
verschiebbare Hülse. In C enthält B die Drehungsachse eines Systemes dreier fest verbundenen Hebel a, b, c, von denen die beiden erstem je ein Gewicht A und A1
tragen, der dritte einen Gleitbacken p, welcher in der
Schleifbahn des Armes K geradegeführt ist.
Bei der Rechtsdrehung des Hebelsystemes a, b, c im Sinne des Pfeiles
der Figur 1
wird der Gleitbacken durch seine feste Bahn an der Abwärtsbewegung gehindert und
statt dessen die Drehungsachse C sammt der Hülse B nach aufwärts gehoben; das umgekehrte findet bei
Linksdrehung des Hebelsystemes statt, und die hieraus erfolgende Hülsenverschiebung
wird zur Bewegung des Regulatorstellzeuges verwendet.
In Folge des hier stattfindenden Zusammenhanges der einzelnen Theile tritt folgende
Gleichgewichtsbedingung für die bewegliche Hülse ein, sobald die Achse Y mit der Winkelgeschwindigkeit ω (g = Acceleration) zu rotiren beginnt:
Textabbildung Bd. 224, S. 20
In dieser Gleichung bedeutet das erste Glied das linkssinnige Drehmoment (nach dem
Pfeile der Figur
1) der Schwungkugeln A und A1, das zweite und
dritte Glied das Drehmoment ihres Eigengewichtes und des Hülsengewichtes, alles
bezogen auf die Drehungsachse C. Die beiden letztern
Ausdrücke sind im Hinblick auf Figur 1 leicht
verständlich. Der Schwerpunkt der Kugeln A. und A1 ist in S, ihr Gesammtgewicht Q, die
Verbindungslinie von S nach C hat die Länge s und den Winkel ψ mit
der Verticalen; somit besteht ein rechtssinniges Drehmoment um die Achse C von der Größe Qs sin ψ.
Das Gesammtgewicht G + Q von
Hülse und Kugeln findet ferner seinen einzigen Stützpunkt durch den Hebel c und Gleiklotz p in dem
Arme K; daher äußert sich der hier auftretende
Widerstand, die Achse C als fest gedacht, im gleichfalls
rechtssinnigen Momente
(G + Q)
c sin (β - ψ)
worin c die Länge des Hebelarmes
von C nach p und β den constanten Neigungswinkel desselben zur
Schwerpunktslinie s bezeichnet.
Der Ausdruck ω2/g
Q r s cos
ψ endlich, welcher das linkssinnige Drehmoment
der Fliehkraft beider Schwungkugeln ausdrückt, constituirt das eigentliche
Charakteristikon des Cosinus-Regulators, mag jedoch erst weiter unten
erörtert und vorläufig als richtig angenommen werden.
Zunächst werde die aufgestellte Gleichgewichtsbedingung aufgelöst in
Textabbildung Bd. 224, S. 20
Wird hier nun β so
gewählt, daß
Textabbildung Bd. 224, S. 21
so vereinfacht sich die Gleichgewichtsbedingung zu
Textabbildung Bd. 224, S. 21
woraus sich der variable Neigungswinkel ψ eliminirt und damit die Winkelgeschwindigkeit
ω gänzlich unabhängig von der Stellung der
Schwungkugeln darstellt. Dieselbe ist vielmehr für gegebene Construction eine
Constante, ausgedrückt durch die Gleichung
Textabbildung Bd. 224, S. 21
derart, daß der Regulator in jeder
Stellung, aber bei nur einer Geschwindigkeit im
Gleichgewicht, somit völlig astatisch ist.
Wird dagegen der Winkel β verändert, so verliert
auch der Regulator die vollkommene Astasie, wie sich aus Auflösung unserer
ursprünglichen Gleichgewichtsgleichung nach ω
ergibt. Hiernach ist nämlich allgemein
Textabbildung Bd. 224, S. 21
In der praktischen Ausführung, wo die Constanten feste Werthe
annehmen und G = 3 Q und c = 1,5s wird, vereinfacht
sich dieser Ausdruck zu
Textabbildung Bd. 224, S. 21
und wird dann nach der oben aufgestellten Bedingung
Textabbildung Bd. 224, S. 21
gesetzt, so wird ω = 40,8
Textabbildung Bd. 224, S. 21, und der Regulator ist astatisch. Der betreffende Winkel arc cos β = 1/6 ist
80° 24′ 21″; sobald derselbe nur um weniges verändert wird,
geht der Regulator der Astasie verlustig. So wird für β = 90° ω = 40,8 Textabbildung Bd. 224, S. 21 und daher die Winkelgeschwindigkeit abhängig vom Ausschlagwinkel ψ. Innerhalb der praktischen Grenzen desselben
von -30° zu +30° wächst ω von 95
auf 104:
für ψ = 0 wird ω = 100
für ψ = -arc tg 6 = -80°
32′ wird ω = 0
für ψ = +90° wird ω = ∞.
Hiernach ist es einleuchtend, wie durch Veränderung des Winkels β der Cosinus-Regulator aus einem völlig
astatischen zu einem beliebig statischen umgewandelt werden kann, und es erübrigt
nunmehr, vor Beschreibung der praktisch durchgeführten Construction, noch die Entwicklung des in unserer
Gleichgewichtsgleichung für Figur 1 aufgestellten
ersten Factors für das Moment der Fliehkraft:
Textabbildung Bd. 224, S. 22
Betrachten wir zunächst das Gewicht A am ersten Arme des
dreiarmigen Hebels der Figur 1. Wenn mit a dessen Hebellänge vom Punkte C, mit φ der Ausschlagwinkel aus der
Verticalen und mit r der feste Abstand der Drehachse C von der mit ω
Winkelgeschwindigkeit rotirenden Regulatorspindel Y
bezeichnet wird, so ist die Fliehkraft der Kugel A
gleich
Textabbildung Bd. 224, S. 22
Hieraus ergibt sich ein linkssinnig wirkendes Drehmoment um
die Achse C gleich
Textabbildung Bd. 224, S. 22
und in gleicher Weise von der Kugel A1 ein im selben Sinne wirkendes
Drehmoment
Textabbildung Bd. 224, S. 22
somit das combinirte Drehmoment beider Kugeln
Textabbildung Bd. 224, S. 22
Um nun ein Cosinuspendel zu bilden, d. h. eine solche
Combination von rotirenden Gewichten, bei welcher für
constante Winkelgeschwindigkeit das Moment der Centrifugalkraft nur dem Cosinus
des Ausschlagwinkels proportional ist, muß die zweite Hälfte des
vorliegenden Ausdruckes gleich Null gesetzt werden:
A a2sin φ cos φ = A1
b2
sin φ1
cos φ1
Dafür ergeben sich sofort die Bedingungen
φ + φ1 = 90°,
Aa2
= A1b2
als entscheidende Merkmale des Cosinuspendels, und das Moment
der Centrifugalkraft wird
Textabbildung Bd. 224, S. 22
Mit diesem Werthe waren wir oben in die Gleichgewichtsgleichung eingegangen und haben
daraus die charakteristischen Eigenschaften des Cosinus-Regulators
entwickelt.
Auf die constructive Durchführung dieses Principes übergehend, genügen wenige Worte
zur Beschreibung.Fig. 2 und 3 zeigt im Verticalschnitt
und Grundriß die Regulatorspindel Y Y, welche am obern
Theile in ein flaches Stück ausgeschmiedet ist, das die Stelle des Armes K der Figur 1 vertritt und mit
dem gleichen Buchstaben bezeichnet ist. Ueber Y
verschiebt sich die aus zwei halbkugelförmigen Hälften zusammengeschraubte Hülse B und wird von einem in K
eingenieteten Stift (linke Seite der Figuren 2 und 3) mitgenommen.
Die untere Hälfte von B trägt beiderseits zwei Lager,
durch welche die Wellen C gesteckt sind, welche je einen
dreiarmigen Hebel tragen. Derselbe muß sich hier dem beschränkten Raume der Hülse
B einfügen und ist daher der Deutlichkeit halber in
Figur 4
bis 6 (etwas
verkleinert) in seinen drei Ansichten herausgezeichnet. Die Anordnung der Gewichte
A und A1 an den Hebelarmen a
und b entspricht vollkommen der principiellen
Darstellung; dagegen ist statt des Gleitbackens p eine
Rolle eingeführt, die in einer Fortsetzung des Gewichtes A1 gelagert ist und auf dem Ansatze K der Regulatorspindel aufläuft. Der principielle
Zusammenhang des Hebelsystems bleibt dadurch selbstverständlich ungestört; indem
aber hier der Laufzapfen der Rolle p in einer
excentrischen Bohrung verdreht werden kann, ist dadurch die Möglichkeit gegeben, den
Winkel β zu verändern.
Die Hülse B findet ihren obern Anschlag in dem Ansatze
der Regulatorspindel, und die untere Begrenzung in einem Bundringe auf derselben;
hier ist auch der Hals in B eingedreht, von welchem die
Stellzeugverbindung zur Drosselklappe oder Expansionsstellung abgeleitet wird.
Die Vorzüge, welche den Cosinus-Regulator in Folge seiner principiellen
Grundlage auszeichnen, sind schon oben hervorgehoben worden; dazu kommt noch der
hier verwendbare große Ausschlagwinkel der Kugeln und entsprechende Muffenhub,
endlich vom constructiven Standpunkt aus die große Einfachheit, welche er selbst vor
dem Watt'schen Pendelregulator voraus hat.
Durch die hohle kugelförmige Hülse, welche den ganzen Mechanismus einschließt, erhält
der Cosinus-Regulator ein sehr gefälliges Aussehen, das ihn besonders
vortheilhaft von der unästhetischen Erscheinung des ältern Buß'schen Regulators
unterscheidet; letzterer ist außerdem bei gleicher Leistungsfähigkeit wesentlich
schwerer, hat geringern Muffenhub und nicht jene constante Energie und gleichmäßige
Empfindlichkeit, welche den Cosinus-Regulator auszeichnet.
Die Fabrikation des Buß'schen Cosinus-Regulators
wurde von der Eisengießerei und Maschinenfabrik H. Gruson
in Buckau bei Magdeburg übernommen.
73. Der Eclipse-Injector.
(Fig. 7
bis 9 [c/3].)
Entsprechend der geringen Anwendung der Injectoren in der amerikanischen Praxis waren
auch nur wenig Ausstellungsobjecte dieser Klasse erschienen. Der interessanteste ist
der so genannte „Eclipse“-Injector — ein
beliebtes Beiwort für „Alles übertreffende“ amerikanische
Erfindungen — welcher in Figur 7 bis 9 dargestellt
ist.
Beim ersten Anblick unterscheidet sich derselbe in nichts von einem gewöhnlichen
Giffard-Injector; — die Nadel ist jedoch nicht verstellbar, sondern
nur um ihre Längsachse drehbar und zieht, anstatt in die Düse einzudringen, dieselbe
mehr oder weniger nahe zu sich heran. Zu diesem Zwecke ist die Austrittdüse mit der
Fangdüse zu einem gemeinschaftlichen Gußstücke vereinigt (Fig. 9), welches in dem
Injectorgehäuse eingeschliffen ist und längs der Spindel dadurch verschoben werden
kann, daß eine rückwärtige Verlängerung eine Mutter trägt, welche das Gewinde der
Spindel umfaßt. Die Mutter und mit ihr der Düsenkörper ist durch zwei vorspringende
Rippen an der Drehung gehindert (Fig. 8) und muß sich daher
beim Drehen der Spindel vor- und zurückschieben.
Hierdurch ist die Stopfbüchsendichtung der Giffard'schen Nadel glücklich vermieden
und außerdem ermöglicht, nach Lösen einer Ueberwurfmutter den Injector zu zerlegen,
ohne die Rohrverbindungen zu stören.
74. Hardick's Niagara-Pumpe.
Figur 10
[b/3].
Besonders bemerkenswerth an dieser direct wirkenden Dampfpumpe ist die einfache
Construction der Saug- und Druckventile; dieselben sind in einem gemeinsamen
Ventilgehäuse zwischen Pumpenkörper und Windkessel angeordnet (Fig. 10) und bestehen aus
hohlen Metallwürfeln, welche in Querwänden des Ventilgehäuses geführt und durch
Anschläge im Hube arretirt werden.
Zu unterst sitzen die Saugventile; sie sind durch eine verticale Zwischenwand von
einander getrennt und communiciren einerseits mit dem Pumpencylinder, anderseits mit
den Eintrittöffnungen e, welche rechts und links am
Cylinder angebracht sind. Ueber den Saugventilen, auf einer horizontalen
Zwischenwand, sind die Drukventile angeordnet und vermitteln den Uebergang des
Druckwassers vom Pumpencylinder in die Austrittöffnungen a des Windkessels.
Durch Lösen eines einzigen, central angebrachten Schraubenbolzens wird der Deckel des
Ventilgehäuses entfernt und der Zugang zu den vier Ventilen hergestellt. Sobald sich
eine Seite der Ventile ausgeschlagen hat, werden sie auf eine andere umgedreht; sind
sie endlich ganz zerstört, so lassen sich neue leicht nachschaffen und in der
Zwischenzeit durch rechteckig behobelte Holzklötze ersetzen.
Der Pumpencylinder ist mit einer Metalllegirung ausgebüchst, der Kolben mit
Compositionsringen gedichtet.
Die Steuerung des Dampfcylinders endlich hat eine gewisse Verwandtschaft mit der Blake'schen Anordnung (*1875 218 14). Das Schiebergesicht trägt einen E-Schieber und neben diesem einen
kleinen, auf der Zeichnung nicht ersichtlichen Hilfsschieber. Im Rücken des E-Schiebers ist ein
Hilfscylinder angebracht, in welchem ein Kolben spielt, jedoch derart, daß der
Kolben durch seine Stange beiderseits im Schieberkasten gehalten ist, und sich daher
der E-Schieber
verschieben muß, sobald am einen oder andern Ende des Hilfscylinders Einströmung,
resp. Ausströmung stattfindet. Dies wird bedingt durch die Stellung des
Hilfsschiebers, welcher, als gewöhnlicher D-Schieber construirt, auf der
Seitenfläche des E-Schiebers sein Schiebergesicht hat und durch Hebelübersetzung
von einem Kreuzkopfe K der Kolbenstange aus hin und her
bewegt wird. In Folge dessen erhält die Pumpe eine größere Länge, gleichzeitig damit
aber auch eine positive Bewegung des Hilfsschiebers, so daß sie von jeder Stellung
aus angelassen werden kann.
75. Van Hagen's Handbohrmaschine.
(Fig. 11
bis 13 [b. c/4].)
Das in den Figuren
11 bis 13 durch drei Schnitte dargestellte Werkzeug, patentirt von demselben
Erfinder, dessen interessante Constructionen wir schon mehrfach (* 1876 222 108. 402) zu beschreiben Gelegenheit hatten,
vereinigt die Vorzüge bequemer Handhabung und schöner Arbeit in sich, welche
bekanntlich der gebräuchlichen Bohrratsche beide völlig abgehen.
Die Hagen'sche Maschine wird in gewöhnlicher Weise über
dem Arbeitsstücke eingespannt, indem der Obertheil entweder gegen einen Bohrwinkel
sich anstemmt, oder in einer Zwinge eingeschraubt wird. Dem entsprechend wird der
aus Fig. 11
und 12
ersichtliche Schlüssel auf die eine oder andere Weise in die aus dem Gehäuse
hervorragende Hülse eingesteckt und der in derselben gelagerte Kern so lange
gedreht, bis die Bohrerspitze in das Arbeitsstück einzudringen beginnt. Dann
ergreift der Arbeiter die in Figur 12 angedeutete
Kurbel und stellt durch continuirliche Drehung derselben das Bohrloch her, ohne sich
weiter mit der
Vorrückung des Bohrers befassen zu müssen, da diese von der Maschine automatisch
besorgt wird.
Zu diesem Zwecke hat die in einem langen Halse gelagerte Spindel der Handkurbel (Fig. 12) außer
dem am Ende befindlichen Kegelrade noch ein Stirnrad aufgesetzt, welches in ein
zweites, seitlich im Gehäuse gelagertes Stirnrad eingreift (Fig. 11) Die Spindel des
letztern trägt weiters eine Schnecke und diese endlich greift in ein Schneckenrad
(Fig. 13
und 12),
welches in der Verticalachse des Gehäuses über dem Bohrkopfe gelagert ist und den
Vorschub besorgt. Indem nämlich das Schneckenrad nach unten ein festes Widerlager
findet, nach oben dagegen mit einer Schraubenspindel verbunden ist, welche in das
Muttergewinde einer im Gehäuse geradegeführten Hülse eingreift, so ist klar, daß
letztere bei Rechtsdrehung der Handkurbel nach aufwärts sich aus dem Gehäuse
herauszuschieben strebt und, hieran durch den Bohrwinkel verhindert, den Bohrer in
das Bohrloch hineinpreßt. Das in die geradegeführte Hülse eingesetzte Mutterstück
muß dabei gleichfalls an der Drehung verhindert werden, was dadurch geschieht, daß
der Schlüssel, welcher zu dessen Einstellung dient, an einem Anschlage arretirt
wird. Ist dagegen die Bohrung vollendet, so wird durch Rückdrehung des Schlüssels
die geradegeführte Hülse wieder in das Gehäuse hineingeschoben, bis die
Handbohrmaschine frei unter dem Bohrwinkel herausgenommen werden kann.
Dieses nette Werkzeug, welches außer der Kurbel, der Bohr- und der
Geradführungshülse alle Bewegungstheile vollkommen geschützt und verborgen hält, ist
selbstverständlich in seinem Grundgedanken nicht neu; aber es zeigt durch die
vollendete Verkörperung dieses Gedankens unläugbar die Hand eines Meisters in
mechanischen Dingen.
(Schluß folgt.)
Tafeln