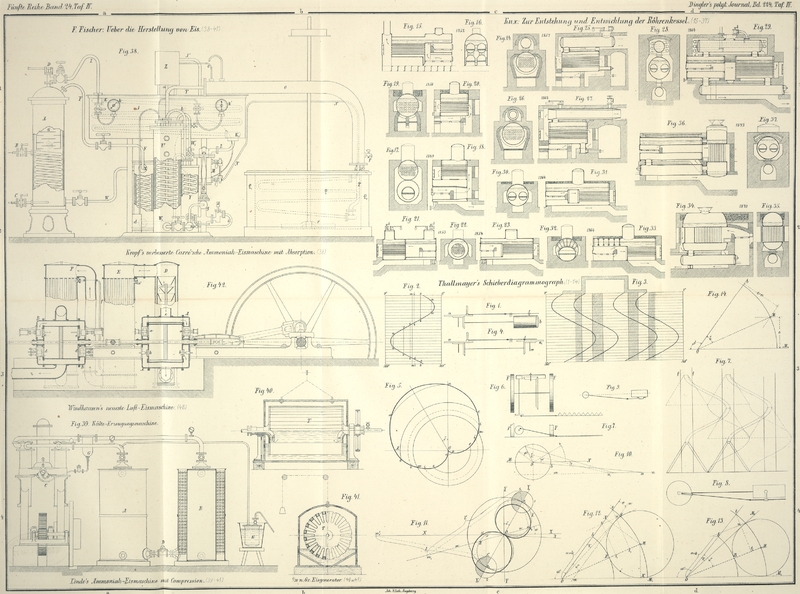
| Titel: | Schieberdiagrammograph von Ingenieur V. Thallmayer, Professor in Ungarisch-Altenburg. |
| Fundstelle: | Band 224, Jahrgang 1877, Nr. , S. 137 |
| Download: | XML |
Schieberdiagrammograph von Ingenieur V. Thallmayer, Professor
in Ungarisch-Altenburg.
Mit Abbildungen auf Taf.
IV [c. d/3].
Thallmayer's Schieberdiagrammograph.
Vornehmlich der Umstand, daß die mathematische Vorbildung der Besucher
landwirtschaftlicher Schulen zum größten Theile eine mangelhafte und der Lehrer
deshalb mehr oder weniger gezwungen ist, sich solcher Mittel zu bedienen, die mit
Umgehung des mathematischen Theiles ein oder das andere Thema aus dem Maschinenbaue
klar machen, veranlaßten mich zur Zusammenstellung des in Figur 1 versinnlichten
Apparates, mit welchem die Schieberbewegung einfach mit einem Stifte auf den
Papiermantel eines mit derselben Winkelgeschwindigkeit wie die Kurbelscheibe a rotirenden Cylinders b
abgeschrieben wird.
Die Excenterstange besteht aus zwei Theilen, um länger oder kürzer gemacht werden zu
können; ferner kann der Kurbelgriff auf verschiedene Excentricität und Voreilwinkel
eingestellt werden, und kann endlich die Kurbel auch bewegt werden, ohne eine
Drehung des Cylinders zu veranlassen, was alles so einfach zu erreichen ist, daß
eine nähere Anführung hier ganz überflüssig erscheint.
Der Apparat, den ich hauptsächlich zur Versinnlichung der Schieberbewegung überhaupt
benutze, kann auch zur Bestimmung der genauen Schieberwege bei kurzen
Excenterstangen gut verwendet werden. Umgibt man nämlich den Cylinder mit einem in
360 gleiche Theile getheilten Papiermantel, stellt ferner die Kurbel auf die
gegebene Excentricität (r) und den gegebenen
Voreilwinkel (δ) ein und beachtet, daß die 0° und 360°
entsprechende Linie, längs welcher der Papiermantel beim Aufsetzen auf den Cylinder
zusammengeklebt wird, unter den Stift s kommt, so erhält
man nach einer vollen Umdrehung der Kurbel und Aufschneiden des Papiermantels nach
der 0°- und 360°-Linie ein Diagramm von der in Figur 2
dargestellten Form.
Zieht man nun in diesem Diagramme die der mittlern Stellung des Schiebers
entsprechende Linie mm und trägt von dieser Linie nach
rechts und links,
wie in Figur
2, die äußere Ueberdeckung e die innere
Ueberdeckung i, sowie die Canalweite a auf, so geben die Entfernungen von den Linien ee, ii bis zur Curve,
bezieh, bis zur Linie aa die Eröffnungen für den
Dampfeintritt und Austritt. Ebenso leicht lassen sich die Winkel für Beginn der
Expansion, Compression etc. mit Leichtigkeit entnehmen.
Man kann auch Diagramme wie Figur 3, welche den ganzen
Schieber in seiner Bewegung darstellen, abnehmen, wenn man Laien die
Dampfvertheilung klar machen will.
Läßt man, wie in Figur 4, unter dem Stifte s eine mit Papier
bespannte Scheibe mit gleicher Winkelgeschwindigkeit wie die Kurbelscheibe rotiren,
so erhält man nach einer vollen Umdrehung der Kurbelscheibe, wenn der Stift s ursprünglich auf den Punkt A (Fig.
5) eingestellt war, auf der Papierfläche eine Curve von der in Figur 5
ersichtlichen Form. Der Punkt A ist von dem Mittelpunkte
der Welle w, um welche die Papierfläche rotirt, grade so
weit entfernt, als die Ausweichung des Schiebers zwischen dem Hubende und der durch
den Voreilwinkel bedingten Stellung beträgt; man stellt nämlich den Stift s zuerst über den Mittelpunkt der Scheibe a1 und führt den Stift
bei verhinderter Drehung der Scheibe a1 auf den Voreilwinkel, worauf er dann über den
Punkt A gelangt.
Beschreibt man nun in Figur 5 vom Punkte O als Mittelpunkt der
mittlern Stellung des Schiebers entsprechend einen Kreis mm und trägt außerhalb und innerhalb seiner Peripherie die Werthe von e, i, a. auf, so geben die radialen Entfernungen von den Kreislinien ee, ii bis zur Curve,
bezieh. Kreislinie aa die Eröffnung für den
Dampfeintritt und Austritt bei den betreffenden Winkeln. Dis Winkel, bei welchen
Beginn der Expansion, Compression etc. eintritt, ergeben sich ebenso einfach wie bei
andern Diagrammen.
Will man die Ausweichungen des Schiebers aus seiner mittlern Stellung in der
Zeuner'schen Diagrammform erhalten, so stelle man den Stift so ein, daß er sich (bei
auf die gegebene Excentricität und das gegebene Voreilen eingestellter Kurbel) vom
Mittelpunkte der Kreisscheibe a1 grade so weit befindet, als die Ausweichung aus
der mittlern Stellung unter diesen Umständen beträgt; nach der darauf folgenden
vollen Umdrehung der Kurbel erhält man die bekannte einem Achter ähnliche Schleife.
Hierbei ist es jedoch nothwendig, die Scheibe a1 zweimal bei verhinderter Drehung der Scheibe a in ihre Anfangslage zurückzuführen, und zwar jedesmal
dann, wenn der Stift s die mittlere Stellung erreicht;
vollführt man die Umdrehung in einem Zuge, so bekommt man auch ein richtiges
Diagramm, jedoch nicht in zweitheiliger Form.
Die Curven, die der Stift s während der Rotation der
Scheibe a1 beschreibt,
übergehen für 1 = ∞ bezieh, in Herzlinie und Kreis.
Der Apparat kann auch zur Verzeichnung jener Curven benutzt werden, in denen sich
jeder Punkt der Mähemaschinenmesser beim Schnitte bewegt. Bei Mähemaschinen wird
während des Fahrens die mit dreieckigen Messern besetzte Messerschiene von einer
Kurbelscheibe mit geringem Hube hin- und herbewegt. Die Kurbelscheibe, deren
Achse höher liegt als die Messerschiene (Fig. 6),wird von den
Fahrrädern F mittels Zahnradübersetzung getrieben. Aus
dem Ubersetzungsverhältnisse n von Fahrrad auf
Kurbelscheibe findet sich der Weg, welchen die Maschine im Fahren in gerader
Richtung während einer Umdrehung der Kurbelscheibe zurücklegt, durch die Formel
2πR/n, wenn R der Radius der Fahrräder ist. Ist nun der Umfang des
Cylinders grade so groß als der Weg 2πR/n, so zeichne man sich an die 0°- und
360°-Linie des Papiermantels die Messer und lasse den Stift aus den
Endpunkten der Messer die Curven beschreiben. Auf diese Weise erhält man ein
Diagramm von der Form der Figur 7, welches die
Schnittverhältnisse klar vor Augen führt. Es versteht sich von selbst, daß zur
Abnahme dieses Diagrammes die Schieberstange seitlich verstellt und der Stift an
einem Arme angebracht werden muß (Fig. 8),auf welche zwei
Erfordernisse der Apparat Figur 1 leicht
eingerichtet werden kann.
Ist der Umfang des Cylinders größer oder kleiner als 2πR/n, so lassen sich behufs Abnahme des
Diagrammes Excentricität und Messerdimensionen leicht dem Cylinderumfange
anpassen.Prof. Dr. Albert Wüst
an der Universität zu Halle a. S. theilte im Praktischen
Maschinenconstructeur 1874 eine Untersuchung des Schnittes der
Mähemaschinenmesser unter der Annahme mit, daß die Messer sich geradlinig im
Zickzack bewegen. Man kann sich den thatsächlichen Verhältnissen auch
dadurch nähern, daß man bei der analytischen Untersuchung die Schnittcurven
nach Umständen als verlängerte oder verkürzte Sinuslinien betrachtet,
worüber ich mir mit Nächstem etwas mitzutheilen erlauben
werde.
Auf der Weltausstellung zu Philadelphia 1876 habe ich an amerikanischen Locomobilen
und halbstationären Maschinen häufig die Beobachtung gemacht, daß die Verlängerung
der Schieberstangenrichtung über oder unter die Kurbelwelle traf, wie in Figur 9 Das
Diagramm der Schieberbewegung kann bei solchen Umständen vom Apparate leicht
abgenommen werden; doch folgt für diesen Fall auch die analytische Untersuchung.
Bedeutet in Figur
10
mn die Schieberstangenachse, MN die Kurbelwellen- resp. Cylinderachse, Ob = r die Excentricität und ba = 1 die Länge der Excenterstange, so befindet sich
der Schieber an einem seiner Hubenden, wenn ab = r mit Ob =1 in einer
Richtung zusammenfällt. Der Winkel, den die Richtung der Excentricität Ob hierbei mit der Cylinderachse bildet, werde mit φ bezeichnet. Der Voreilungswinkel sei δ.
Nach einer Drehung der Kurbel um den Winkel ω ist
aa1 der Schieberweg
vom Hubende a an gerechnet. Aus Figur 8 findet sich
leicht:
Textabbildung Bd. 224, S. 140
Der Schieberweg ξ von der
mittlern Stellung des Schiebers findet sich durch die Gleichung:
Textabbildung Bd. 224, S. 140
welcher Gleichung für ω =
0 und ω = 180 gleiche, dem Zeichen nach
verschiedene Werthe entsprechen.
Bestimmen wir noch den Hub des Schiebers; er ist das Maximum von aa1. Es ergibt sich aus
d (aa1)/d
ω = 0 die Gleichung (ω + δ) 1 + r/1 - r
sin φ zur Bestimmung
jenes Werthes von ω, bei welchem aa1 zum Maximum wird. Nach Einsetzung des Werthes cos (ω + δ) in
die Gleichung I ergibt sich der Hub h:
Textabbildung Bd. 224, S. 140
Aus Gleichung III ergibt sich, daß bei den in Rede
stehenden Verhältnissen der Hub des Schiebers grüßer ausfällt als wie die zweifache
Excentricität; denn Gleichung III wird, wie dies aus d(III)/d(φ) = 0 resultirt und wie es der zweite
Differentialquotient erkennen läßt, für φ = 0 zu
einem Minimum, nämlich zu 2r.
Bezeichnet man mit ωh den Winkel, welchen die Excentricität
durchlaufen muß, um den Schieber vom Hubende a auf das
andere Ende des Hubes zu bringen, so findet man zu seiner Bestimmung die
Gleichung
Textabbildung Bd. 224, S. 140
ωh nimmt für den Werth φ = 0 die Größe von 180° an; sonst ist
der Werth von ω kleiner als 180°, auch
ein Punkt, worin diese Anordnung von der gewöhnlichen abweicht.
Ist nun bei einem gewissen Werthe von φ (der stets klein ist) das Verhältniß
von r zu l so groß, daß der
Werth von l als ∞ betrachtet werden kann, so geht
nach Einsetzen von 1=∞ die Gleichung II zunächst
in die unbestimmte Form ∞×0 und dann in die Gleichung Textabbildung Bd. 224, S. 141 über, woraus zu ersehen, daß der Schieber unter den berührten
Verhältnissen sich so verhält wie ein Schieber, auf welchen die Excentricität r/cosφ und der Voreilwinkel (δ + ∞) einwirken.
Das entsprechende Kreisdiagramm läßt sich demnach für diesen Fall auf die
gewöhnliche Art verzeichnen. Für den Werth 1=∞ wird noch h=2r/cos φ und sin (ωh-φ) = rsinφ oder ωh =
180°
Kann das Verhältniß 1/r nicht als ∞ betrachtet
werden, so ergeben sich die genauen Schieberwege entweder mittels Berechnung aus
Gleichung II oder durch Construction dieser
Gleichung.
Man zeichne wie in Figur 11 zwei Linien XX und YY
unter rechtem Winkel und unter dem Winkel δ an YY die Linie Y1Y1 trage vom Scheitel dieses Winkels auf letzterer Linie nach beiden
Seiten die Excentricität r auf, beschreibe aus den
Endpunkten o1
o2 der Excentricität mit
dem Radius (1 + r) sinφ die zwei Kreise 1 und 2, schlage endlich über r als Durchmesser die zwei Kreise I und II.
Um den Schieberweg nach einer Drehung der Kurbel um den Winkel ω zu finden,
zeichne man an XX unter dem
Winkel ω die Linie m n, verbinde den Punkt s1 auf Kreis l mit o1 und verlängere diese Richtung, bis sie in s1 die Peripherie des
Kreises 1 schneidet. Vom Punkte s1 schneide man auf der Richtung mn mit der Länge der
Excenterstange l ein, um den Punkt m1 zu bekommen. Trägt
man von diesem an bis s2
die Länge
Textabbildung Bd. 224, S. 141
welche sich durch Construction leicht findet, auf, so ist O s2 die gewünschte
Ausweichung des Schiebers aus seiner mittlern Stellung. Der Beweis für die
Richtigkeit der Constrution ist leicht geführt; es ist:
Textabbildung Bd. 224, S. 141
und nachdem Os = r sin (ω + δ), ist
auch
Textabbildung Bd. 224, S. 142
was zu beweisen war.
Um nun weiter die Curve für den Hin- und Hergang des Kolbens zweitheilig zu
bekommen, bestimme man die übrigen Punkte s2 für die Winkelwerthe von ω = 0 bis
180° mit Beachtung des Umstandes, daß für die Punkte s1 stets solche Punkte zu nehmen sind, die
auf der von der Linie XX
links liegenden Hälfte des Kreises 1 gelegen sind, welche Hälfte in Figur 11 schraffirt
erscheint. Für die Werthe von ω = 180° bis 360° finden sich die
Punkte s2′ auf
dieselbe Weise und gilt bezüglich der Punkte s1′ und des Kreises 2 dasselbe wie oben.
Bei der gewöhnlichen Anordnung fallen die Punkte, wo die Curven die XX-Achse schneiden,
auf einen und denselben Ort, ob nun die Excenterstange unendlich lang oder ob sie
von endlicher Länge ist. Dies trifft bei der eben behandelten Anordnung nicht zu,
wie man sich durch Einsetzen von ω = 0 und ω = 180 in die Gleichung
II überzeugen kann. Je kürzer die Excenterstange,
desto weiter fallen die erwähnten Punkte aus einander, und sind sie einander am
nächsten, wenn 1 = ∞ wird. Hierüber gibt der erste und die weitern
Differentialquotienten der Gleichung II (nach Einsetzung
von ω = 0) Aufschluß; für 1 = ∞ wird nämlich bei ω = 0
Gleichung II zu einem Minimum.
Die Winkelwerthe, für welche sich der Schieber in seiner mittlern Stellung befindet,
ergeben sich aus Gleichung II, nachdem sie gleich Null
gesetzt wurde.
Mit Hilfe des besprochenen Apparates können die Diagramme bei bekannten
Schieberdimensionen namentlich für kurze Excenterstangen, die Steuerung mag nun aus
einem einfachen Schieber oder aus zwei Schiebern (Georges, Breval, Gonzenbach u. A) bestehen, leicht abgenommen werden, ebenso auch in
verjüngtem Maße das Diagramm für die Bewegung des Kolbens. Der Apparat kann, um in
der Längsausdehnung an Raum zu sparen, auch so eingerichtet werden, daß die
Schieberstange, statt vom Verbindungsgelenk an der Excenterstange sich weiter nach
vorwärts zu erstrecken, nach rückwärts geführt wird; auch können statt conischer
Räder Frictionsräder in Anwendung kommen.
Zur Bestimmung von gewissen Bedingungen entsprechenden Schieberdimensionen ist der
Apparat wohl nicht geeignet; doch können die gewöhnlichen, beim Entwürfe einfacher
Schiebersteuerungen vorkommenden Fälle auf sehr einfache Weise auch anderweitig
gelöst werden und zwar:Vgl. Zeuner: Schiebersteuerungen, 4.
Auflage.
1. Soll mit einem einfachen Schieber ein gegebenes Expansionsverhältniß ε bei
gegebenem Voreilen v erzielt werden und ist außerdem
noch die Canalweite a, sowie die Strecke k, um welche die äußere Schieberkante bei der größten
Ausweichung des Schiebers noch hinter die innere Kante des Eintrittscanales
zurückweichen soll, gegeben, so kann man sich behufs Bestimmung der Excentricität
r, des Voreilwinkels δ der äußern
Ueberdeckung e und des Voröffnungswinkels γ
folgenden einfachen Constructionsverfahrens bedienen: Man zeichne in Figur 12 den dem
Expansionsverhältnisse ε entsprechenden Winkel ω′ trage auf
seinen Schenkel Ot das Stück a + k auf und beschreibe damit als Radius den
Bogen bB, zeichne ferner in der Entfernung v, eine Linie parallel zu Ot. Legt man nun in den Winkel nmM1 einen Kreis, der die beiden Schenkel nm und nM1, sowie auch den Bogen bB berührt, so ist die Strecke MO von seinem
Mittelpunkte M bis zum Punkte O gleich r, ferner MOt=δ und MB = e, was in folgendem erwiesen ist.
Aus der Figur läßt sich entnehmen, daß: r = a + k + e und MN = tt1 + e + v = r
sin δ und MN1 = e = r
sin (ω1 + δ) ist. Ebenso ist noch ss1 = ut1,=e und tu = v, mithin alle Bedingungen erfüllt.
Als Voröffnungswinkel findet sich der Winkel γ=t
Og Ergänzt man die Figur zum Reuleaux'schen Diagramm, so läßt sich alles
Nöthige auch daraus unmittelbar entnehmen.
2. Ist a, und k, sowie der
Voröffnungswinkel γ und das Expansionsverhältniß ε gegeben, so ergeben
sich die andern Dimensionen, wie folgt: Man zeichne Figur 13 den dem
Expansionsverhältnisse entsprechenden Winkel ω′ und an seinen Schenkel
den Voröffnungswinkel γ, ziehe mit Ob = a +k als Radius den Bogen
bB, lege in den Winkel M0OM1 einen Kreis, der außer seinen beiden Schenkeln
auch noch den Bogen bB berührt, so ist, wenn M der Mittelpunkt dieses Kreises ist, MO = r, M B = ut1 = e,
tu = v und tOM=δ. Die Richtigkeit des Angeführten findet
sich wie oben.
3. Ist v, ε und e
gegeben, so zeichne man den Winkel ω′ (Fig. 14), ziehe in der
Entfernung e+v eine
Parallele zum Schenkel Ot, in der Entfernung e eine Parallele zum Schenkel OM1, und es ist dann, wenn M der Durchschnittspunkt der beiden Parallelen ist, M O = r und tOM=δ.
Tafeln