| Titel: | Cycloïdenzirkel von Prof. V. Thallmayer. |
| Fundstelle: | Band 224, Jahrgang 1877, Nr. , S. 386 |
| Download: | XML |
Cycloïdenzirkel von Prof. V. Thallmayer.
Mit Abbildungen auf Taf.
IX [a/4]
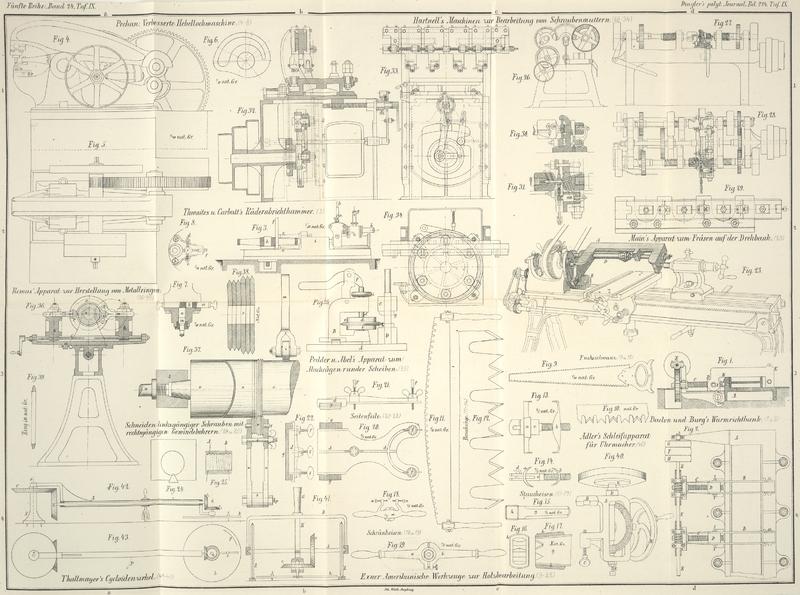
Thallmayer's Cycloïdenzirkel.
Im Anschluß an die Beschreibung des Epi- und Hypocycloïden-Zirkels von
Dr. Plettner in Stralsund
(*1876 219 304) erlaube ich mir nachstehend, die
Construction eines von mir entworfenen Cycloïdenzirkels anzuführen, ferner ein
Instrument, das zur Verzeichnung gemeiner Cycloïden verwendet werden kann.
Das Instrument zur Verzeichnung gemeiner (auch verkürzter und verlängerter gemeiner)
Cycloïden besteht, wie aus Figur 41 ersichtlich, aus
einer in den mit Griff G versehenen Bügel B eingelassenen Querachse A,
die an ihren Enden Laufräder L trägt. Ein aus zwei
gleich großen conischen Rädern c, c1 bestehendes Räderpaar überträgt die durch Ziehen
des Instrumentes auf Schienen eingeleitete Rotationsbewegung auf die Kreisscheibe
k. Von der Mitte des Bügels erstreckt sich ein Arm
H nach unten, welcher, in geeigneter Weise geformt,
das conische Rad c1
aufnimmt und auch der Welle A das Vorbeipassiren
gestattet. Der in der Kreisscheibe k befindliche Stift
s beschreibt nun je nach Umständen eine gemeine,
eine gemeine verkürzte oder eine gemeine verlängerte Cycloïde. Ist nämlich die
Entfernung des Stiftes s vom Mittelpunkte der Scheibe k (bei gleich großen Rädern c,
c1) gleich dem Halbmesser r der Laufräder, so beschreibt er bei der Rotation eine
gemeine Cycloïde; ist diese Entfernung kleiner als r, so
beschreibt er eine verkürzte, und ist sie größer als r
eine verlängerte Cycloïde.
Der Zirkel zur Verzeichnung von Epi- und Hypocycloïden (auch verkürzten und
verlängerten Epi- und Hypocycloïden) ist in Fig. 42 und 43 dargestellt
und hat folgende Einrichtung. Auf dem Ständer S ist ein
conisches Rad C befestigt; der horizontale Arm A mit den beiden conischen Rädern c und c1 ist
mittels eines Bügels drehbar um die senkrechte Achse des Ständers S aufgehängt und trägt an seinem Außenende noch das
conische Rad c2, sowie
die Kreisscheibe k, in der sich ein Stift in
verschiedenen Abständen vom Mittelpunkte einsetzen läßt.
Wird nun der Arm A im Kreise herumgeführt, so wälzt sich
das conische Rad c; am Rade C ab, und es wird auch die Scheibe k mit dem
Stifte s zur Umdrehung veranlaßt. Dreht man den Arm A in der Richtung des Pfeiles P, so kommt die Scheibe k in der durch Pfeil
p angedeuteten Richtung zur Rotation, d. i. so, als
ob sie am Arme A geführt, sich an dem innern Umfange
eines Kreises abwälzen würde, und es wird demnach der Stift s eine Hypocycloïde beschreiben.
Ist nun R der Halbmesser des Rades C, r der Halbmesser des Rades c, r1 der Halbmesser der Räder c1 und c2, ρ die
Entfernung des Stiftes s vom Mittelpunkte o1, der Kreisscheibe k und endlich die Entfernung os = ρ1, so ist nach einer Drehung des Armes A um
den Winkel φ die Abwälzung des Rades c am Rade
C gleich R φ und
auch Rφ = rφ1; hieraus folgt φ1 = R/r φ und die Verdrehung des Stiftes s aus seiner Anfangslage gleich ρφ1. Ist nun ρ1φ=ρφ1, so
wird der Stift s eine gewöhnliche Hypocycloïde
beschreiben; ist ρφ1
ρ1φ, so
wird er eine verkürzte, und ist endlich ρφ1ρφeine verlängerte Hypocycloïde beschreiben.
Ist das conische Rad C unterhalb des Rades c angebracht, so dreht sich bei derselben
Drehungsrichtung des Armes A wie vorher die Scheibe k so, als ob sie am Arme A
geführt, sich an der Außenperipherie eines Kreises abwälzen würde, und es wird der
Stift s eine Epicycloïde beschreiben. Das Uebrige
verhält sich ähnlich wie im vorigen Fall.
Es lassen sich beide Zirkel auch zu einem vereinigen; auch läßt sich durch Versetzen
des Stiftes und dadurch, daß man statt der Kegelräder cylindrische Frictionsteller
und Scheiben in Anwendung bringt, um die Uebersetzungsverhältnisse durch einfaches
Verschieben der Scheiben c und c2 an der Welle A ändern zu können, der Variation genug Spielraum eröffnen. Aehnliches gilt auch
in Bezug des Instrumentes zur Verzeichnung gemeiner Cycloïden. Ebenso ließe sich der
Arm A auch zum Verschieben einrichten, um ihn länger
oder kürzer machen zu können.
Tafeln