| Titel: | Die Beurtheilung der Reinheit des Schnittes von Mähemaschinen; von Prof. V. Thallmayer. |
| Autor: | V. Thallmayer |
| Fundstelle: | Band 224, Jahrgang 1877, Nr. , S. 573 |
| Download: | XML |
Die Beurtheilung der Reinheit des Schnittes von
Mähemaschinen; von Prof. V.
Thallmayer.
Mit Abbildungen auf Texttafel B.
Thallmayer, über die Reinheit des Schnittes von
Mähemaschinen.
Im Anschluß an die Bemerkung S. 139 dieses Bandes bringe ich nachstehend eine
eingehende Untersuchung über die Reinheit des Schnittes bei Mähemaschinen.
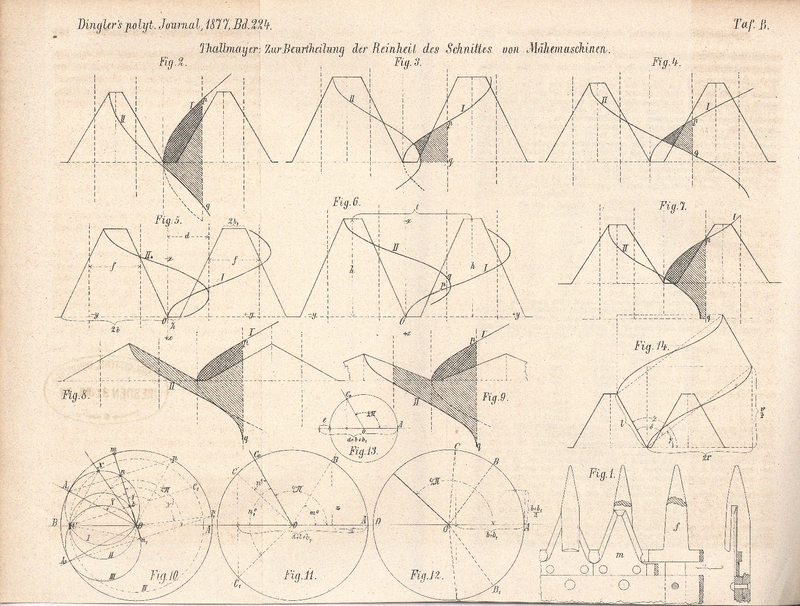
Figur 1
veranschaulicht die Messer m, welche während des
Vorwärtsganges der Maschine, durch eine Kurbel in hin- und hergehende
Bewegung versetzt, die Halme an den Kanten der Finger f
abschneiden. Die Kurbelscheibe, deren Welle zumeist höher liegt als die
Messerschiene, wird auf die früher näher angegebene Weise durch Zahnradübersetzung
vom Fahrrade der Maschine in Umdrehung versetzt.
Auf jede Kurbelumdrehung entfällt ein gewisser Vorwärtsgang der Maschine; bezeichnet
man ihn mit v, so ist v =
πD/n, wenn D den Durchmesser
des Fahrrades und n die Uebersetzungszahl vom Fahrrade
auf die Kurbelscheibe bedeutet. Da bei Mähemaschinen der Kurbelarm klein, die
Kurbelschiene in den meisten Fällen lang und die Höhe der Kurbelwelle über die
Messerschiene im Verhältnisse zur Kurbelschienenlänge nicht bedeutend ist, so kann
man annehmen, daß jeder Punkt des Messers beim Schneiden eine Sinuslinie
durchläuftAls Curicsum sei hier angeführt, daß in der Monographie „Die
Mähemaschinen“ von Emil Perels
(Jena 1869) diese Curve als Schraubenlinie bezeichnet wird.,
welche je nach dem Verhältnisse der Peripherie des Kurbelwarzenkreises zu dem auf
eine Kurbelumdrehung entfallenden Vorwärtsgange der Maschine eine verlängerte oder
verkürzte sein kann.
Jede der Figuren
2 bis 9 weist zwei Curven auf; die mit I
bezeichnete entspricht der Bewegung des Messers von links nach rechts, wobei die
rechtsseitige Messerkante schneidet; die mit II
bezeichnete Curve hingegen entspricht der grade vorher vollführten Bewegung des
Messers von rechts nach links, wobei die linksseitige Messerkante die schneidende
war. Aus den betreffenden Figuren ist zu ersehen, daß die auf der einfach
schraffirten Fläche stehenden Halme von dem Messer, namentlich wenn es nicht mehr
scharf sein sollte, statt abgeschnitten zu werden, von der Fingerkante blos
weggebogen werden, um dann im Vereine mit den auf der doppeltschraffirten Fläche
stehenden Halmen nach vorwärts gebogen und endlich an der Fingerkante abgeschnitten
zu werden. Fig.
5 und 6 weisen keine solchen, die Reinheit des Schnittes und die Gleichheit der
Stoppelhöhe beeinträchtigenden Partien auf, weil in dem einen Falle die zwei Curven
sich grade auf der Fingerkante schneiden und im andern Falle der Schnittpunkt q der Curve II mit der
Fingerkante höher liegt, als wie jener p der Curve I.
Um nun für irgend eine Mähemaschine angeben zu können, in wie weit die Reinheit des
Schnittes beeinträchtigt erscheint, erweist es sich als erwünscht, die Lage der
Durchschnittspunkte der Curven I und II, sowie die der Durchschnittspunkte der Curven mit der
Fingerkante zu kennen. Der Ort dieser Durchschnittspunkte läßt sich, wie aus
Nachfolgendem zu ersehen sein wird, auf leichte Weise durch Construction bestimmen.
Für die Bezeichnung der Messer- und sonstiger Dimensionen sind folgende
Bezeichnungen gewählt worden:
r die Länge des Kurbelarmes,
b die halbe untere Messerbreite,
b1 die halbe obere
Messerbreite,
z unterer Zwischenraum zweier Messerkanten,
h Messerhöhe,
d die Entfernung des untersten schneidenden Punktes der
Messer von der Fingerkante, wenn die Kurbel am todten Punkte steht,
f Breite der Finger,
t Fingertheilung,
v Vorwärtsgang der Maschine während einer
Kurbelumdrehung,
ψ Verhältnißzahl zwischen Messerhöhe (h) und halbem Vorwärtsganges(v/2).
Die Curven I und II sind im
Verlaufe der nachfolgenden Untersuchungen stets auf das in den Figuren 5 und 6 ersichtlich
gemachte rechtwinkelige Coordinatensystem bezogen. Zur Auffindung der Abscissen (xI. . xII. .) der
Durchschnittspunkte der Curven I und II mit der Fingerkante zeichne man einen Kreis mit dem
Radius r (Fig. 11), trage von A gegen den Mittelpunkt hin die Länge d auf und bestimme durch Errichtung einer Senkrechten
auf den Durchmesser im Endpunkte dieser Länge den Winkel AOB. Ist seine Größe in Graden m, so ist:
xI =
v m/360 und x′I = - v
m/360.
Trägt man ferner die Länge d + b + b1 von A. aus auf dem Durchmesser auf und bestimmt man auf
ähnliche Weise wie oben den Winkel COA und C1OA, so ist, wenn nach
Einzeichnung des Winkels ψπ die Differenz
COA. - ψπ
= n Grade, C1OA - ψπ = n′ Grade ausmacht:
xII =
v n/360 und x′II = v
n′/360.
Das Vorzeichen der zwei Werthe für xII bestimmt sich nach dem Vorzeichen der Differenz der beiden
Winkelwerthe COA und ψπ.Das Vorzeichen der Abscissen xII und x′II kann man übrigens
auch aus der Lage des Winkels ψπ
erkennen; ist in Figur 11 der
Werth von ψπ kleiner als AOC, so haben beide positives Vorzeichen; ist
ψπ gleich AOC, so ist eine von ihnen Null, die andere
positiv; ist ψπ größer als AOC und kleiner als 180°, so ist die
kleinere negativ, die größere hingegen positiv; ist ψπ gleich 180°, so sind beide gleich und
haben entgegengesetztes Vorzeichen; liegt ψπ zwischen 180 und AOC1, so ist die kleinere positiv,
die größere negativ; ist ψπ = AOC1, so ist
eine Null, die andere negativ; ist endlich ψπ größer als AOC1, so sind beide negativ. Ist die
Länge d + b + b1 größer als 2r, so ist (Fig. 13) die Entfernung
zwischen dem Fußpunkte der aus dem Punkte C0 auf den Durchmesser errichteten Senkrechten und
dem Endpunkte der Länge d + b + b1 gleich
dem Abstande des Schnittpunktes der Curve II mit der Y-Achse von der Fingerkante, und das Stück e gleich der Entfernung des Scheitelpunktes der Curve
II von der Fingerkante.
Um die Coordinaten der Durchschnittspunkte der Curven I
und II, von denen die Abscissen mit α1, α2 die Ordinaten
mit β1,β2 bezeichnet
sein mögen, zu erhalten, zeichne man einen Kreis mit r
als Halbmesser, trage an AO den Winkel ψπ auf, halbire den Winkel 180 —
ψπ und zeichne über seiner
Halbirungslinie in der Ausdehnung von OA1 = r als Durchmesser
den Kreis I, übertrage BA1 nach BA2 und zeichne ähnlich wie oben Kreis III. Dann zeichne man über OC als Durchmesser den Kreis II. Nimmt man nun
b + b1/2 in den Zirkel und schneidet es von O bis b als Sehne des
Kreises II ab, und verlängert man diese Sehne bis m und n1, so sind mn = β1 und mn1 = β2 die Ordinaten
der Durchschnittspunkte. Um nun auch die Abscissen der Durchschnittspunkte zu
bekommen, errichte man in den Punkten n und n2 Senkrechte auf n1m. Dieselben schneiden
die Kreisperipherie in den Punkten p
und p1. Ist γ das Maß des Winkels mOp, γ′ jenes des Winkels mOp1, in Graden, so
find die Abscifsen:
α1 = v
γ/360 und α2 = v
γ′/360.
Um nun die Lage der Durchschnittspunkte in Beziehung auf die Y-Achse zu erfahren, zeichne man (Fig. 12) einen Kreis mit
dem Radius r, trage von A
auf einer auf den Durchmesser in diesem Punkte errichteten Senkrechten das Stück b+b1/2 als Sinus eines Winkels auf, verdopple diesen
Winkel bis B und trage ihn gleichzeitig auch auf die
untere Seite bis B1,
über und ziehe die Radien OB und OB1. Gleichzeitig trage man von A auf dem Durchmesser AO das
Stück b + b1 auf, errichte im Endpunkte desselben auf AO eine Senkrechte und verbinde ihre Durchschnittspunkte
C und C1 mit der Kreisperipherie mit dem Mittelpunkte O. Zeichnet man nun an den Radius AO den Winkel ψπ in den Kreis,
so ergeben sich zwischen ψπ den Winkeln
AOB, AOB1, AOC, AOC1 bezüglich des
Vorzeichens der Abscissen α1, und α2, wenn unter α1 die numerisch kleinere und unter
α2 die
numerisch größere Abscisse verstanden wird, Relationen, die, wegen leichterer
Uebersicht in eine Tabelle zusammengefaßt, hier erscheinen:
Textabbildung Bd. 224, S. 576
Werth von ψπ; Vorzeichen von α1; Vorzeichen von α2;
Anmerkung.; Findet kein Schnitt statt.; Findet Berührung statt.; Die Curven
schneiden sich im Coordinatenursprunge.; Beide Abscissen an Größe gleich.; Die
Curven schneiden sich im Coordinatenursprung.; Findet Berührung statt.; Findet
kein Schnitt statt.
Die mit * bezeichneten Fälle sind für Mähemaschinen, da sie schlechte
Schnittverhältnisse geben, nicht gut verwendbar und womöglich auszuschließen. Es
zeigen dies auch die Figuren 2, 8 und 9.
Beim Entwürfe von Mähemaschinen können nur die übrigen Fälle Berücksichtigung finden,
davon die letzteren auch nur im beschränktem Maße, weil sonst die Messer zu lange
werden; es zeigt dies Figur 6, in welchem Falle
ψ = 1,48 oder ψπ = 266° ist.
Zur Bestimmung der bis jetzt gefundenen Größen ist es hinreichend, den
Kurbelwarzenkreis blos einmal aufzuzeichnen, indem sie alle aus einem Kreise
entnommen werden können; nur wurde hier der bessern Uebersicht wegen der Kreis
dreimal gezeichnet.
Die Richtigkeit der vorstehenden Behauptungen läßt sich folgendermaßen nachweisen.
Die Gleichungen der Curven I und II mit Bezug auf das oben angenommene Coordinatensystem sind, wenn man
unter m das Verhältniß des Umfanges des
Kurbelwarzenkreises zu dem während einer nämlich Kurbelumdrehung stattfindenden
Vorwärtsgange der Maschine versteht, m = 2πr/v nimmt,
für die Curve I
Textabbildung Bd. 224, S. 577
für die Curve II
Textabbildung Bd. 224, S. 577
Setzt man statt y den Werth d
in diese beiden Gleichungen und bezeichnet d/r mit γ, hingegen b+b1/r mit w, so findet man
leicht:
Textabbildung Bd. 224, S. 577
Setzt man x = 0 in die Gleichung (2), so findet man y =d+(b+b1) - r(1 - cosπψ), und setzt man für x den Werth (v/2 - h) in die Gleichung (2), wird y = 2r - (b+b1), womit alles in
Bezug auf die constructive Ermittlung der Werthe von xI und xII Behauptete erwiesen ist. Die Richtigkeit der
Ermittlung des Vorzeichens der Werthe von xII und x′II folgt unmittelbar aus dem obigen Ausdrucke für
xII.
Zur Bestimmung derjenigen Strecke pq (Fig. 2 bis 9), durch welche die den
Fingerkanten zunächst stehenden Halme nach vorwärts gebogen werden, hat man pq = xII + xII oder
Textabbildung Bd. 224, S. 577
Nachdem nach dieser Formel der Werth von pq zu Null wird,
wenn
Textabbildung Bd. 224, S. 577
wird, so ist dies gleichzeitig auch die Bedingung für das
Nichteintreffen des Borwärtsbiegens.
Ist der vorstehende Ausdruck > ψ so findet
Vorwärtsbiegen statt; ist hingegen derselbe < ψ, so wird pq negativ und es tritt kein
Vorwärtsbiegen ein, weil dann der Schittpunkt der Curve II mit der Fingerkante höher liegt als jener der Curve I.
Ist 1 - γ 1 - w > 1
oder r - d - (b + b1) r, d. h. schneidet
die Curve II die Fingerkante nicht, so ergibt sich pq, wie dies auch aus Figur 7 zu entnehmen:
Textabbildung Bd. 224, S. 578
Der Fall, daß Curve I die Fingerkante nicht schneidet,
kommt bei Mähemaschinen nicht vor.
Aus Gleichung (1) und (2) ergeben sich für die Coordinaten α1, β1, α2, β2 der Durchschnittspunkte der zwei
Curven I und II nach einigen
Reductionen der Werthe:
Textabbildung Bd. 224, S. 578
Berücksichtigt man, daß b + b1/r = w, mh/r = ψπ, r/m = v/2π ist und drückt die Functionen von ψπ durch jene des halben Winkels aus, so
erhält man nach einigen Reductionen:
Textabbildung Bd. 224, S. 578
Streng genommen ist:
Textabbildung Bd. 224, S. 578
wobei für n die Werthe von
0 bis α einzusetzen wären; hier aber kommt es nur auf die kleinsten
Werthe von α1 und α2 an.
Nun ist in Figur
10 Winkel A1OC = 90 - ψπ/2, und da OA1 = r ist, so ist OC = r
sin
ψπ/2, mithin, da Ob = b + b1/2 gemacht wurde,
Textabbildung Bd. 224, S. 578
Zieht man durch den Punkt C den Kreis IV, so ist leicht zu entnehmen, daß Winkel A1ON = A1OC = 90-ψπ/2,
sein müsse.
Bezeichnet man den Winkel A1On mit φ,
so wird Winkel mON = φ - 90 + ψπ/2, und
nachdem NCn = mON ist als
Peripheriewinkel, die auf demselben Bogen aufruhen, so ist auch nCN. = φ - 90 + ψπ/2.
Es ist NCC1 = A1On = φ, weil ihre Schenkel auf
einander senkrecht stehen, mithin nCC1 = NCC - = φ - φ + 90 -
φπ/2 = φπ/2 Demnach nb = C btg (90 - φ/2) = Cbcotg
φ/2 und nach Einsetzung des oben für Cb gefundenen Werthes: Textabbildung Bd. 224, S. 579
Nun ist mn = r - Ob - bn und nach Einsetzung
der Werthe für Ob und bn
Textabbildung Bd. 224, S. 579
Daß mn1 = β2 ist, erweist
sich auf ähnliche Art: COA2 = COA1 = 90
- φπ/2, mithin, da Cn1A2 = COA1 = 90 - φπ/2 ist, auch n1Cb = 90 - φπ/2, mithin bn1 = bn; da
ferner mn1 =r + On1 = r + bn1 - Ob, so ist auch
Textabbildung Bd. 224, S. 579
Weiters findet man
Textabbildung Bd. 224, S. 579
womit die Richtigkeit der früher zur Ermittlung von α1, β1, α2,
β2, angegebenen
Construction erwiesen ist.
Nun ist noch der Beleg für das im Vorstehenden angewendete Kriterium zur Beurtheilung
des Vorzeichens der Abscifsen α1 und
α2 zu geben; unter einem sei bemerkt, daß
die Ordinaten β1
und β2, wie dies
Gleichung (6) unmittelbar erkennen läßt, stets nur positives Vorzeichen haben
können.
Aus Gleichung (5) folgt, daß, wenn w = 2 sinφπ/2 oder
Textabbildung Bd. 224, S. 579
Berührung stattfindet.Streng genommen sollten diese Werthe eigentlich2nπ + arc cos (1 - w2/2) und 2
(n + 1)π
- arc cos (1 - w2/2),
ebenso2nπ + arc cos (1 - w) und 2 (n + 1) π - arc cos (1 - w)geschrieben werden, wobei für n alle Werthe von 0 bis ∞ einzusetzen wären; hier aber
kommen nur die kleinsten Bogenwerthe in Betracht. Nun ist in Fig. 12
AB = 2rarc sin
b + b1/2r = 2rarc sinw/2; mithin entspricht AOB =
ψπ und AOB1 = ψπ in der That der Berührung der Curven.
Aus (5) folgt ferner, dass wennTextabbildung Bd. 224, S. 579 und demnach,
wie man nach einigen Reductionen findet, w = 2 sin2ψπ/2
oder ψπ = 2 arc sinTextabbildung Bd. 224, S. 580 = arc cos (1 -
w) = 2 π
arc cos (1 - w) ift, bie Curven sich im Coordinatenursprunge
schneiden. Vgl. die Note 3 auf S. 479.
Da nun in Figur
12
Textabbildung Bd. 224, S. 580 ist, so findet für ψπ = AOC und ψπ =
AOC1 wirklich
Schnitt der Curven im Coordinatenursprunge statt. Ferner ergibt sich aus Gleichung
(5), daß für den Fall als ψ = 1 wird, die
Abscissen der Durchschnittspunkte gleich groß und entgegengesetzt im Vorzeichen
sind. Läßt man nun ψ kleinere Werthe als 1
annehmen, so wird die negative Abscisse kleiner, die positive größer, bis die
negative zu Null und die positive zum Maximum geworden ist (entspricht dem Schnitt
im Coordinatenursprung). Nimmt nun ψ noch weiter
ab, so fallen beide Durchschnittspunkte in das positive Viertel des
Coordinatensystemes, bis sie für Textabbildung Bd. 224, S. 580 in dem Berührungspunkte zusammenfallen. Wird nun ψ größer als 1, so findet grade das Entgegengesetzte des eben
Gesagten statt, und somit ist die Richtigkeit des in Anwendung gekommenen Kriteriums
auch erwiesen. Daß für den Fall, als der Schnitt im Coordinatenursprung stattfindet,
die Ordinate zum Maximum wird, findet man leicht durch Differentiation der Gleichung
(6); es erhellt dies übrigens auch aus den beiden Gleichungen α1 + α2 = v/2 und α1 + α2 = 2 r - (b + b1), welche man bei etwaiger Bestimmung der
Coordinaten der Durchschnittspunkte der Curven durch Rechnung mitbenutzen kann, und
von welchen Gleichungen letztere unmittelbar aus Gleichung (6) folgt, erstere sich
aber leicht aus Gleichung (1) und (2) herleiten läßt.
Das Kriterium für die Vorzeichen der Abscissen ließe sich, falls man den Weg der
Rechnung beträte, nach obigem leicht aufschreiben, doch um an Raum zu sparen,
unterbleibe es hier.
Beim Vergleiche verschiedener Mähemaschinen auf die Reinheit des Schnittes kann die
Fläche f, durch welche mangelhaftes Schneiden
stattfindet, in Verhältniß zu jener Fläche F gebracht
werden, welche von der Messerkante bei einem einfachen Hübe befahren wird. Für die
Fläche F findet man, wie dies aus Figur 14 leicht zu
entnehmen, Textabbildung Bd. 224, S. 580 wobei l die Länge der Messerkante bedeutet. Es
ist noch δ= ψ - φ und tgφ = v/4r.
Die Fläche f läßt sich, um Integrationen auszuweichen,
annähernd genug entweder als Dreieck oder als Polygon berechnen, nachdem man
letzteren Falles sich ein oder zwei Zwischenpunkte in den Curven bestimmt hat. Doch
gibt auch die alleinige Bestimmung der Strecke pq
zumeist einen richtigen Maßstab zur Beurtheilung der Reinheit des Schnittes bei
Mähemaschinen, und für diesen stellte zuerst Prof. Dr.
A. Wüst (Mähemaschinen der Neuzeit, Leipzig 1875) die
nachfolgenden Näherungsformeln auf, welche unter der aus Einfachheitsrücksichten
getroffenen Annahme, daß der Schnitt nach geraden Zickzacklinien stattfindet,
abgeleitet sind. Wüst findet nämlich:
Textabbildung Bd. 224, S. 581
und
Textabbildung Bd. 224, S. 581
Von diesen beiden Formeln soll die obere zur Anwendung kommen,
wenn r klein ist, d. h. wenn die Messer blos durch einen
Finger schneiden, die untere aber, wenn r groß ist, d.
h. wenn die Messer durch zwei Finger schneiden. Wäre nun
Textabbildung Bd. 224, S. 581
so wären die Formeln (8) und (9) mit der oben gefundenen
Formel (3) ganz identisch.
Will man nun eine Näherungsformel zur Bestimmung von pq
aufstellen, obwohl dies die Einfachheit der Formel (3) gar nicht nothwendig
erscheinen läßt, so verfährt man der Natur der Sache nach viel angemessener, wenn
man in Formel (3) die Werthe von arc
cos (1 - γ) und arc cos (1 - γ - w) durch ihre
Reihen ausdrückt und die dritten und weitern Potenzen von (1 - γ) und (1 - γ - w) vernachlässigt. Man bekommt dann
unmittelbar
Textabbildung Bd. 224, S. 581
welche Formel für alle jene Fälle, wo die Curve II die Fingerkante noch schneidet, was stets dann
eintreten wird, wenn 2r > d
+ b + b1, ist, für pq Werthe
gibt, welche den wirklichen Werthen sehr nahe kommen müssen, da die vernachlässigten
Glieder zumeist Potenzen echter Brüche sind. Aus dieser Formel folgt sofort, daß das
Vorwärtsbiegen gleich Null wird, wenn Textabbildung Bd. 224, S. 581 ist. Wird dieser Ausdruck > ψ, so
findet stets Vorwärtsbiegen statt; wird er < ψ, so ist pq negativ und es findet kein
Vorwärtsbiegen statt.
Sollte die Curve II die Fingerkante nicht schneiden, was
der Fall sein wird, wenn 2 r < d + b + b1 ist, so setze man in Formel (4) für arc cos (1 - γ) den Reihenwerth ein, und man erhält dann
unmittelbar
Textabbildung Bd. 224, S. 581
welche Formel auch für den Fall benutzt werden kann, wenn 2r = d + b + b1 ist, d. h. die Curve II die Fingerkante eben berührt.
Um nun entnehmen zu können, inwieweit die nach diesen verschiedenen Formeln
berechneten Werthe von pq, nämlich des Vorwärtsbiegens
beim Schnitte von links nach rechts, sich von einander unterscheiden, so sind, da
ein directer Vergleich der Formeln unter einander nicht gut thunlich erscheint, in
nachstehender Tabelle verschiedene theils extreme, theils gewöhnlich vorkommende
Messer- und sonstige Dimensionen angenommen, und es erscheinen die nach den
Formeln (8) und (9) berechneten Werthe von pq darin mit
fetten Zahlen gedruckt.
Textabbildung Bd. 224, S. 582
v; h; z; t; f; d; b; b1; r; pq (3); pq (8, 9); pq (10)
Aus dieser Tabelle ist, wie nicht anders zu erwarten war, zu ersehen, daß die nach
Formel (10) bestimmten Werthe von pq für die Zwecke der
Praxis mehr als ausreichend mit den nach Formel (3) bestimmten übereinstimmen. Man
kann wohl auch die nach Formel (8, 9) bestimmten noch als brauchbar hinnehmen; doch
gestattet diese Formel und ihre Herleitungsweise keinen besonders klaren Einblick in
die Verhältnisse die bei Behandlung des vorliegenden Themas berücksichtigt werden
müssen. Endlich erlaube ich mir noch zu bemerken, daß die am angeführten Orte
geäußerte Ansicht Dr. Wüst's,
daß die sachgemäße Behandlung dieses Themas, nämlich die Miteinbeziehung der
Kurbelbewegung in die Untersuchungen complicirte Formeln im Gefolge habe, dem
Vorstehenden nach eine nicht begründete ist.
Ist ω bedeutend größer als die Einheit, so ist es
angezeigt, den Werth von pq nach Formel (3) zu
berechnen.
Sonstiges auf dieses Thema Bezug habendes, sowie die Verwendung der im Vorstehenden
enthaltenen Diagramme und Gleichungen zur Gewinnung von passenden Verhältnißzahlen
zum Entwurfe von Mähemaschinen werde ich in einem nächsten Aufsatze folgen
lassen.
Ungarisch-Altenburg, April 1877.
Tafeln