| Titel: | Ueber das Taseometer und Versuche mit demselben; von Ingenieur Friedr. Steiner, Docent am Wiener Polytechnicum. |
| Autor: | Friedrich Steiner |
| Fundstelle: | Band 226, Jahrgang 1877, S. 283 |
| Download: | XML |
Ueber das Taseometer und
Versuche mit demselben; von Ingenieur Friedr. Steiner, Docent am
Wiener Polytechnicum.
Mit Abbildungen im Text und
auf Taf. VI [d/4].
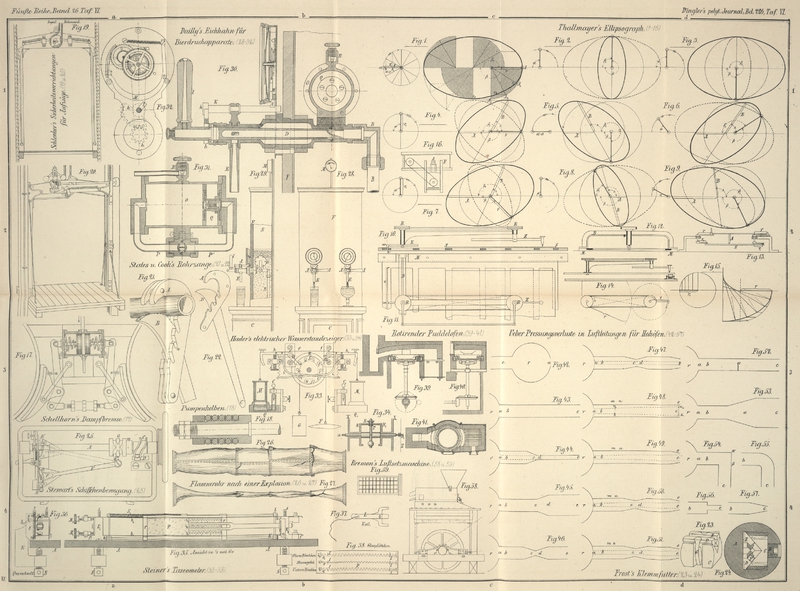
Steiner's Taseometer.
Die Unsicherheit, welche stets in der Berechnung und Prüfung
auszuführender Bauconstructionen liegt, gab wohl feit langem
Veranlassung, auf Methoden zu sinnen, die eine directe Messung
der auftretenden Kräfte gestatten. Besonders wichtig erscheint
diese Frage für den Brückenbau.
Man hat zu diesem Zwecke an Stelle einzelner Theile Dynamometer
eingeschaltet, oder wohl auch, wie dies durch Dupuy geschehen ist, mit Hilfe eines
Fühlhebels direct die Ausdehnung und Zusammenziehung einzelner
Stäbe gemessen und dadurch auf die Beanspruchung geschlossen.
Die Resultate, welche aus diesen Experimenten erhalten
wurdenVgl. Notice sur les dessins, modèles et
ouvrages etc. réunis par les soins du ministère
des traveaux publics. Exposition universelle à Vienne
en 1873 (Paris, Imprimerie
nationale), p. 430., zeigten, daß die in den Gitterstäben einer Brücke
hervorgerufenen Kräfte kaum die Hälfte der Werthe von jenen
betrugen, welche sich auf Grund der gewöhnlich zur Anwendung
kommenden Formeln ergaben, ja daß gegen die Mitte des Balkens
jene Stäbe, welche nach den Unterstützungspunkten hin abfallen,
Zugspannungen aufwiesen, während in den andern von
entgegengesetzter Neigung Druckkräfte zur Geltung kamen, was den
Hypothesen, welche die Theorie aufstellt, gradezu
widerspricht.
Auch ich habe mich seit langem mit der Idee getragen, irgend eine
empfindliche Methode für die directe Messung zu finden. Die
unharmonischen Töne eines Claviers, das bei plötzlich
eingetretenem Witterungswechsel durch Verziehen des Holzes
verstimmt worden war, riefen in mir den Gedanken wach, ob es
nicht möglich wäre, aus der Aenderung des Tones auf die
Veränderung der Inanspruchnahme des Holzes zu schließen. Dieses
Princip näher verfolgend, construirte ich zwei Klammern, die ich
an einen Stab schraubte, und über welche ich eine Saite spannte.
Versuche zeigten mir bald, daß die Aenderung der Belastung des
Stabes sofort Tondifferenzen hervorrief. Durch Prof. Rebhann, dem ich meine Versuche
mittheilte, wurde ich auf die mir damals noch unbekannten
Versuche und Schlüsse Göbbel's
aufmerksam gemacht, der es schon 1863 probirt hatte, die Größe
der Spannung einzelner Bestandtheile in Eisenconstructionen
durch die Töne daran angebrachter Eisendrähte direct zu
messen.Vgl.
Bericht über die 14. Versammlung Deutscher Architekten und
Ingenieure, abgehalten zu Wien 1864 (Verlag des österreichischen
Ingenieur- und Architektenvereines), S. 167. Die
Hauptresultate seiner Versuche waren, daß bei den Be- und
Entlastungen jeder bestimmten Belastung ein bestimmter Ton, der
mit der Belastung höher wurde, entsprach; daß die Temperatur
zwischen 12 und 16° ohne wesentlichen Einfluß blieb; und
daß um so kleinere Belastungsunterschiede merkbar wurden, je
tiefer der Ton war.
So interessant nun auch die vorgelegten Methoden sein mögen, so
leiden sie doch an zwei wesentlichen Gebrechen. Das erste
besteht darin, daß man zur Vergleichung der Tonhöhen an das
Gehör des Experimentators, welches nur bei wenigen Personen die
hierfür nöthige Empfindlichkeit besitzt, angewiesen ist, und daß
diese Methode bei über die Brücke rollenden Eisenbahnzügen,
deren Einfluß man constatiren will, absolut unbrauchbar sich
erweisen dürfte; das zweite, daß nur die Zusammenziehung oder
Ausdehnung des ganzen Stabes gemessen wird, nicht aber örtlich
auftretende Spannungen bestimmbar sind.
Indem ich das obgenannte Princip beibehielt, suchte ich beide
Uebelstände zu beseitigen und construirte nach manchen Versuchen
für das Polytechnicum zu Hannover den in Fig. 35
bis 38
skizzirten Apparat.Derselbe wurde in seiner gegenwärtigen Form von dem
Mechaniker Leo Elger, dem ich manche
praktische Idee hinsichtlich der Detaildurchführung verdanke,
hergestellt. Ein anderer in den Details bedeutend abweichender
Apparat wurde in der Wochenschrift des österreichischen
Ingenieur- und Architektenvereines, 1877 S. 13 ff.
beschrieben.
Auf dem zu untersuchenden Stabe oder Stabbestandtheil A werden zwei Klammern K₁ und K₂ durch Anziehen der Klemmschrauben S befestigt. Die Klammern sitzen mit
glatt gehobelten Flanschenflächen f
auf, während durch Feststellen der Schräubchen s, von denen je zwei hinter einander auf
jeder Klammer sich befinden, die Angriffspunkte bestimmt und
eine Ebene fixirt werden. (Es sei hier ein für allemal bemerkt,
daß natürlich die Form der Klammern und ihre Einspannung eine im
Allgemeinen veränderliche, nach dem Querschnitte der zu
untersuchenden Stabstelle sich richtende sein kann.) Ueber beide
Klammern legen sich zwei Stahlbändchen b₁ und b₂, aus
feinen englischen Uhrfedern gebildet; dieselben laufen über
ausgefeilte Stege, sind an einem Ende mittels Schräubchen
befestigt und können an dem andern durch die Mikrometerschrauben
M₁ und M₂, deren bewegliche Muttern die weiteren
Befestigungsschräubchen tragen, angespannt werden. An die
Bändchen sind zwei feine Stahlschreibfederchen z₁ und z₂ angelöthet. Die Klammer K₂ trägt eine Stimmgabel, deren eine Zacke
ebenfalls mit einem Schreibfederchen z versehen ist. Mit beiden Klammern steht ein Rahmen in
Verbindung, der mittels zweier in k
und k' lose sitzenden Kugelgelenke
eine Drehung um die Achse kk'
zuläßt und durch einen federnden Hebel h in beliebiger Lage erhalten werden kann. Der Rahmen
trägt einen Schlitten r, in welchen
man ein berußtes Glasplättchen P
(Fig. 38)
schiebt. Eine Spiralfeder zieht den Schlitten, wenn er sich frei
überlassen wird, stets gegen K₁.
Führt man den Schlitten ganz nach rechts, bringt das berußte
Glasplättchen zur leichten Berührung mit den Spitzen der
Federchen und steckt unmittelbar rechts neben den Federchen,
senkrecht zur Ansichtsfläche, einen Keil L (Fig. 37),
welcher, sich zwischen die Zacken der Stimmgabel und die
gespannten Bändchen klemmend, diese aus einander zwängt, so wird
hierdurch der Schlitten in seiner Lage erhalten. Zieht man dann
den Keil mittels einer daran angebrachten Schnur rasch heraus,
so gerathen sowohl die Bändchen als auch die Gabelzacken in
Schwingungen; die an den Federchen anliegende Glastafel wird im
Schlitten von der Spiralfeder rasch vorüber geführt, und es
entsteht auf der berußten Fläche ein Bild der
Schwingungsverhältnisse; man erhält ein Phonogramm.
Die Stimmgabel ersetzt die Uhr, sie dient als zeitmessendes
Instrument. Nimmt man ein Phonogramm vor, eines nach der im Stabe
A eingetretenen Beanspruchung auf,
so kann man aus beiden die Größe der Beanspruchung von A direct berechnen, wie ich in Folgendem
zeigen will.
Hat sich der Stab gedehnt, so wird die ursprüngliche
Schwingungszahl der Bändchen eine größere, hat er sich
zusammengedrückt, eine kleinere werden. Hat sich der Stab
gebogen, so wird, im Falle dies z.B. nach abwärts geschehen ist,
das obere Bändchen verhältnißmäßig mehr an Tonhöhe, bezieh.
Schwingungszahl abnehmen als das untere.
Fig. I und II (S. 286) zeigen Theile zweier
Phonogramme, wie dieselben thatsächlich gelegentlich eines
Versuches erhalten wurden, bei dem das Instrument an einem Stabe
befestigt war.
Die Sinuslinie 0 zeigt in beiden Fällen die Schwingungen der
Stimmgabel, 1 jene des obern, 2 jene des untern Bändchens. Im
ersten Falle kommen auf 40 Schwingungen der Stimmgabel 25
Schwingungen des obern, 20 Schwingungen des untern Bändchens, im
zweiten auf 40 Schwingungen der Stimmgabel 20,5 des obern, 20,3
des untern Bändchens. Der Stab hat sich daher – in
horizontaler Lage betrachtet – jedenfalls nach abwärts
gebogen, gleichzeitig hat derselbe aber auch, da sich die
Schwingungszahl des untern vermehrt, einen Zug
erlitten. Die nähere Berechnung der factischen Beanspruchung
müßte nach den später zu entwickelnden Formeln erfolgen.
Fig. 1., Bd. 226, S. 286
Fig. I;
Phonogramm für den unbelasteten Zustand.
Fig. 2., Bd. 226, S. 286
Fig. II;
Phonogramm im belasteten Zustande.
Durch Anfertigung eines dritten Phonogrammes nach entschwundener
Beanspruchung wird man sich überzeugen, ob die Bändchen nicht
etwa durch ein Nachgeben an den Einspannungsstellen ihre
ursprüngliche Schwingungszahl verändert haben, was bei präciser
Ausführung des Instrumentes nicht zu erwarten steht und auch bei
meinen Versuchen nicht eintrat.
Theorie des Instrumentes. Wir wollen
annehmen, daß das Instrument an einem Stabe befestigt sei,
dessen Querschnittsfläche gegen jene der StahlbändchenHierbei
sind, um einen richtigen Maßstab für die Beurtheilung des
Fehlers zu gewinnen, die Querschnittsflächen der Bändchen noch
mit dem Verhältniß des Elasticitätscoefficienten des Stahls zu
jenem des Stabmateriales zu multipliciren; ein Coefficient, der
bei Schmiedeisen 1,25, bei Holz 21 beträgt. sehr
groß ist, und daß dasselbe hinsichtlich des Trägheitsmomentes
des Stabquerschnittes in Betracht zu den Trägheitsmomenten der
Bandquerschnittsflächen, bezogen auf die Stabquerschnittsachse,
gelte; es ist dann gestattet, jenen Theil der innern Kräfte,
welcher von den Bändchen bei der Beanspruchung des Stabes
aufgenommen wird, gegen jene des Stabes zu vernachlässigen, was
in den allermeisten praktischen Fällen eintritt.
Betrachten wir zunächst ein Bändchen b₁. Es bedeute in Figur
III:
P₁ die
Kraft, mit der dasselbe ursprünglich angespannt wurde,
g die
Beschleunigung der Schwere,
G₁ das
Gewicht des Bändchens innerhalb der Stege,
l₁ die
Länge des Bändchens zwischen den Stegen,
l'₁ und l''₁ die über die Stege
greifenden Längen.
Fig. 3., Bd. 226, S. 287
Fig. III.
Die Anzahl der Hin- und Herschwingungen n₁ in der Secunde sind dann gegeben durch
1) n₁
= 1/2 √(gP₁)/(G₁ l₁).
Macht die Stimmgabel n Schwingungen in der Secunde, und
setzen wir n₁/n = v₁, so ergibt sich aus (1) sofort, daß
2) v₁² = g/(4 G₁ l₁ n²) P₁.
Bedeutet nun ferner P'₁ die
Kraft, womit das Bändchen während der Beanspruchung des Stabes
angespannt wird, so ist die Verlängerung Δl₁, die dasselbe erfährt, gegeben durch
3) Δl₁ = (P'₁ – P₁)/E₁f₁ (l₁ + l'₁ + l''₁),
wenn E₁
den Elasticitätscoefficienten, f₁ die Querschnittsfläche des Bändchens ausdrückt.
Macht der zwischen die Stege gespannte Theil nun n'₁ Schwingungen in der Secunde,
so ist n'₁ = 1/2 √(gP'₁)/(G₁ l₁). Quadrirt
man diese Gleichung, dividirt sie beiderseits durch n² und zieht Gleichung (2) davon
ab, so erhält man, das Verhältniß n'₁/n mit v₁ bezeichnend:
4) v'₁² – v₁² = g/4G₁l₁n² (P'₁ – P₁),
oder mit Rücksicht auf (3)
5) Δl₁ = C₁ (v'₁² – v₁²),
wenn man unter C₁ = (4 l₁(l₁ + l'₁ + l''₁) G₁ n²)/(gE₁ f₁) eine vom Material und den
Dimensionen des Bändchens abhängige Constante versteht.
Fig. 4., Bd. 226, S. 288
Es sei nun (Fig. IV) wieder A der zu beanspruchende Stab, an welchem
das Instrument befestigt wurde; I, II zeige die gegenseitige
Lage der Einspannungsquerschnitte vor
der Beanspruchung von A; I, II' die
gegenseitige Lage derselben nach
eingetretener Beanspruchung des Stabes. Hierbei sind abweichend
von der Figur in Wirklichkeit die Aenderungen natürlich sehr
klein gegen die ursprüngliche Länge, so daß es gestattet ist,
den Bogen für die Sehne zu setzen. Bezeichnet man den
KrümmungsradiusStrenge genommen, ist natürlich diese Größe der
Krümmungsradius der elastischen Linie der eingespannten Strecke
nur, wenn dieselbe ein Kreisbogen, angenähert dann, wenn l gegen die Länge des Stabes klein
ist. des Stabes nach eingetretener Beanspruchung mit
r, die Verlängerung, welche das
obere Bändchen erlitten, mit Δl₂, jene des untern mit Δl₁, die Abstände der
Bänder von der Oberfläche des Stabes mit a₂ und a₁, so
ist, wie sich aus der Aehnlichkeit der Dreiecke abo und acO sofort ergibt: l/r = (Δl₂ – Δl₁)/(a₂ – a₁). Bezeichnet man wie früher mit
v₁ und v₂ die Verhältnisse der Schwingungszahlen der
Bändchen 1 und 2 zu den Stimmgabelschwingungen vor, mit v'₁ und v'₂ die
analogen Verhältnisse nach
eingetretener Beanspruchung von A,
mit C₁ und C₂ die diesbezüglichen
Constanten, so ergibt sich, mit Rücksicht auf (5):
Textabbildung Bd. 226, S. 289
ein Ausdruck, welcher uns direct
gestattet, aus den beobachteten Größen v'₂, v₂, v'₁, v₁ auf die Krümmung des Stabes zu schließen. Sind
die beiden Bändchen gleich lang und aus demselben Material, so
ist C₁ = C₂. Der Ausdruck wird positiv,
wenn der Krümmungsmittelpunkt unter,
negativ, wenn er über den
schwingenden Bändchen liegt.
Die Längenänderung Δl
z einer Faser, die den
Abstand z von dem obern Bändchen
hat, ist, wie sich aus der Figur leicht ergibt: Δl z = Δl₂ – (l/r) z.
Die Beanspruchung K z auf die Quadrateinheit in
dieser Faser ergibt sich demnach, wenn E den Elasticitätscoefficienten des Stabes bezeichnet,
Kz = (Δl z/l) E,
oder
7) K z = (v'₂²
– v₂²) C₂ E/l – l/r E/l z.
Ist die Dicke des Stabes an den Einspannungsstellen d, so ergibt sich hieraus speciell als
Beanspruchung
der obersten Faser: K' = (v'₂²
– v₂²) C₂ E/l – l/r E/l a₂ und
für die
unterste: K'' = (v'₂² – v₂²) C₂
E/l
– l/r E/l (a₂ + d).
Man ist hiernach im Stande, direct aus den beobachteten Größen
die Beanspruchung irgend einer Faser des Querschnittes zu
berechnen. Dem positiven Zeichen entspricht Zug, dem negativen
Druck.
Einfluß der Temperatur. Wenn möglich,
wird es sich empfehlen, die nöthigen Versuche bei nahe gleicher
Temperatur anzustellen. Sind jedoch Temperatursdifferenzen
unvermeidlich, so läßt sich denselben in nachstehender Weise
Rechnung tragen.
Es sei t die Temperatur, bei der man
den ersten Versuch (A unbeansprucht)
gemacht; t' die Temperatur im
Momente des zweiten Versuches bei beanspruchtem Stabe. Die
Differenz t' – t werde mit Δt bezeichnet. Wir setzen wieder voraus, und dies
wird in den meisten praktischen Fällen zutreffen, daß die
Querschnitte der Bändchen sehr klein gegen den Querschnitt des
Stabes seien; es wird sich dann der Einfluß der Bändchen auf den
Stab vernachlässigen lassen.
In Folge der Temperatursänderung hat sich l am Stabe geändert um Δl = αl
Δt, wenn α den Ausdehnungscoefficienten
des Stabes bezeichnet; das Bändchen würde sich frei ausdehnen um
αl' = α'l Δt;
durch die Differenz beider Ausdehnungen Δl – Δl'
wird demnach in dem Bändchen l eine
thatsächliche Längenänderung erzeugt, welche gegeben ist durch
(α – α') Δtl₁. Hierdurch erleidet aber das Quadrat
der Schwingungszahl des Bändchens einen Zuwachs, welcher, in
Verhältniß zu n gesetztMit sich
ändernder Temperatur wird allerdings auch die Schwingungszahl
n der Stimmgabel eine andere. Die
Abweichung ist jedoch eine ganz verschwindende und wird auch bei
feinen physikalischen Untersuchungen innerhalb gewöhnlicher
Temperatursverhältnisse wohl kaum in Betracht gezogen. und mit Δ (v'₁²) bezeichnet, nach (5)
gibt: Δ (v'₁²) = (α – α')Δtl₁)/C₁.
Sind die Länge, das Material und der Querschnitt des Bändchens 2
dieselben wie jene des ersten, so ist der Zuwachs, welchen die
Länge des ersten Bändchens durch die Temperatur erfährt, gleich
dem des zweiten. Unter obiger Annahme, die sich bei jedem
Instrumente erfüllen läßt, bleibt der Werth l/r
unverändert derselbe, da die Correctionsglieder sich aufheben.
Auf Formel (6) ist daher die Temperatur ohne Einfluß; (7) aber
geht mit Rücksicht auf die Temperatursdifferenz Δt über in:
8) K z = (v'₂²
– v₂²) C₂ E/l – l/r E/l z – (α – α')
Δt E.
Besteht das Versuchsstück aus Schmiedeisen, das schwingende
Bänderpaar aus Stahl, so ist α = 0,00001232, α' = 0,00001239, E =
2000000 (für Kilogramm und Qudratcentimeter). Dies gibt für die
Größe des Correctionsgliedes + 0,14 Δt, oder für eine Temperatursdifferenz von
10° 1k,4 für
1qc, d. i. 1/3000 des
Festigkeitscoefficienten, also eine hier wohl nicht zu
berücksichtigende Größe.
Bedeutender wird der Einfluß, wenn das Versuchsmaterial Holz ist;
setzt man hier α = 0, E = 120000, so erhält man + 1,49 Δt; dies gibt für eine Differenz
von 10° 14k,9
oder 1/57 des Festigkeitscoefficienten. In diesem Falle wäre
also wohl auf den Temperaturwechsel Rücksicht zu nehmen.
Bestimmung der Constanten. Die
Ermittlung der in den Formeln auftretenden, von der
Beschaffenheit der schwingenden Bändchen abhängigen
Constanten kann in verschiedener Weise geschehen, am einfachsten
wohl dadurch, daß man sich direct der Mikrometerschräubchen zur
Anspannung der Bändchen bedient. Die am beschriebenen
Instrumente befindlichen Schrauben besitzen eine Ganghöhe von
genau 0mm,5. Nach
Formel (5) ist aber Δl₁ = C₁
(v'₁² – v₁²); dies gestattet
direct eine Bestimmung der Größen C₁ und C₂.
Betrachten wir zunächst ein Bändchen. Nimmt man für eine
bestimmte Stellung der Mikrometerschraube, die eine hinreichende
Anspannung des Bändchens erzielt, ein Phonogramm auf und
ermittelt v₁, verlängert dann
das Bändchen um 0mm,5,
indem man die Mikrometerschraube um eine volle Windung dreht,
und nimmt abermals ein Phonogramm auf, so ist die Verlängerung,
die das Bändchen innerhalb der Stege erfahren: 0,5 – C₁ (v'₁² – v₁²). Daraus berechnet sich aus den
bekannten Werthen von v'₁ und
v₁ unmittelbar C₁ =
0,5/(v'₁² – v₁²) Millimeter. In ganz
ähnlicher Weise erfolgt die Bestimmung von C₂.
Am vorliegenden Instrumente ergab sich aus 2 Versuchen
folgendes.
Oberes Bändchen.
Erster
Versuch.
Zweiter
Versuch.
Ursprünglicher
Stand:
n₂ = 24,5
n
= 60,5
n₂
= 30,5
n
= 74,8
Schraube um
360° gedreht:
n'₂ = 28,8
n'
= 45,9
n'₂
= 49,8
n'
= 79,0.
Unteres Bändchen.
Ursprünglicher
Stand:
n₁ = 25
n
= 60,5
n₁
= 30,5
n
= 74,8
Schraube um
360° gedreht:
n'₁ = 28,8
n'
= 45,9
n'₁
= 49,2
n'
= 79,0.
Daraus berechnen sich die Werthe für den
ersten Versuch:
Oberes Bändchen.
v'₂
=
n'₂/n' =
28,8/45,9
=
0,6274 und v₂ = n₂/n =
24,5/60,5 = 0,4033.
C₂
=
0,5/(v'₂² – v₂²)
=
0,5/(0,3937 – 0,1627) = 2mm,165.
Unteres Bändchen.
v'₁
=
n'₁/n' =
28,8/45,9
=
0,6274 und v₁ = n₁/n = 25/60,5
= 0,4132.
C₁
=
0,5/(v'₁² – v₁²)
=
0,5/(0,3937 – 0,1707 = 2mm,242.
Für den zweiten Versuch:
Oberes Bändchen.
v'₂
=
n'₂/n' =
49,8/79,0 = 0,6304 und v₂ = n₂/n =
30,5/74,8 = 0,4077.
C₂
=
0,5/(v'₂² – v₂²) = 0,5/(0,3974 – 0,1662)
= 0,5/0,2312 = 2mm,163.
Unteres Bändchen.
v'₁
=
49,2/79,0 = 0,6228 und v₁ = 30,5/74,8 =
0,4077.
C₁
=
0,5/(v'₁² – v₁²) = 0,5/(0,3879 – 0,1662)
= 0,5/0,2217 = 2mm,255.
Als mittlere Werthe ergeben sich demnach: C₂ = 2mm,164 und C₁ = 2mm,248. Da a₂ – a₁ = 47 – 11,75 = 35mm,25 ist, ergibt die
Formel (6):
l/r = 0,0614 (v'₂² – v₂²) – 0,635 (v'₁² – v₁²).
Mit Hilfe des bekannten Werthes der Constanten ist es nunmehr
auch leicht, die Ausdrücke, nach denen die Berechnung der
Beanspruchung K' und K'' der obersten und untersten Faser an
der Einspannungsstelle zu geschehen hat, anzugeben.
Die Substitution der früher erhaltenen Werthe
in die Formel für K' und K'' gibt für die oberste, bezieh.
unterste Faser:
K' = [0,00746 (v'₁² – v₁²) – 0,00180 (v'₂² – v₂²)] E, beziehungsweise
K'' =
[(0,00746 + 0,000159 d) (v'₁² – v₁²) – (0,00180 +
0,000154 d) (v'₂² – v₂²)] E.
Beispiel. Um den
Gebrauch des Instrumentes zunächst an einem einfachen Versuche
zu erproben, wurde nachstehendes Experiment gemacht. Ueber zwei
auf festen Unterlagen ruhenden Schneiden von 1m Entfernung wurde ein
Stahlstab von 80mm
Breite, 8mm Höhe und
1500mm Länge
symmetrisch gegen den Halbirungspunkt der Auflagerdistanz
gelegt. Je 50mm von den
Enden des Stabes wurden zwei Wagschalen aufgehängt, unmittelbar
neben jede der Klammern des Instrumentes kam je eine
empfindliche Libelle, nun wurde das Taseometer (ebenfalls
symmetrisch gegen die Stabmitte) an demselben angeschraubt,
jedes der Bändchen angezogen, der Stand der beiden Libellen
beobachtet und notirt, und ein Phonogramm aufgenommen; dasselbe
ergab n₁ = 45,2, n₂ = 34,5 und n = 80. Hierauf wurde in die Wagschalen
je ein Gewicht von 3k
gelegt, der Ausschlag der Blasen an den Libellen markirt und
abermals ein Phonogramm aufgenommen; dasselbe ergab n₁ = 46,5, n₂ = 40,2 und n =
80.
Um über den Winkel ins Klare zu kommen,
welcher der Differenz der Ausschläge entspricht, wurde derselbe
Ausschlag mit Hilfe eines Justirbretchens erzeugt. Die
dreimalige Beobachtung und Berechnung dieses Winkels ergab:
Libelle 1.
Libelle 2.
4' 52''4' 45''4'
52''
4'
50''5' 8''5' 00''
im Mittel
588''
oder0,00285.
Die Berechnung dieses Werthes nach
Formel (6) aber liefert unter Berücksichtigung der oben
gefundenen Werthe:
v'₁² =
0,3379
v₁² = 0,3185
v'₂² = 0,2525
v₂² = 0,1860.
Daraus findet man φ = 0,0614
× 0,0665 – 0,0635 × 0,0194 = 0,00285, was
mit dem oben ermittelten Werthe vollständig übereinstimmt.
Einfluß der Fehler. Es möge im
Weiteren die Genauigkeit etwas näher untersucht werden, welche
sich mit dem vorliegenden Instrumente erreichen läßt. Setzen wir
zunächst den Fall voraus, daß wir es mit der Untersuchung eines
Stabes zu thun haben, der nur auf Zug beansprucht wird. Man
braucht sich dann nur eines Bändchens zu bedienen, und hat K = C₂ (v'₂²
– v₂²) E/l für l/r = 0; für
unser Instrument ist C₂ =
2mm,164 und l = 400mm.
Setzen wir ein Versuchsstück aus Eisen voraus und dabei E = 20000, so wird
(α) K = 108 (v'₂² – v₂²).
Die beiderseitige Differenzenbildung gibt
ΔK = 216 (v'₂ Δv'₂ – v₂ Δv₂).
Nun ist aber v₂ = n₂/n,
daher Δv₂ = (Δn₂ n – Δnn₂)/n².
Die Länge einer Stimmgabelwelle beträgt durchschnittlich 2mm, wobei 80 Wellen noch
mit voller Schärfe auf die Tafel kommen. Nimmt man den Werth der
Schätzung in der Längenmessung mit 0mm,1 an, so ist Δn = ± 0,05 einer
Stimmgabelwellenlänge. Die Wellenlänge eines Bändchens ist 1/v mal so groß als jene durch die
Stimmgabel erzeugte; wir können daher näherungsweise Δn₂ = ∓ v₂ Δn setzen. Δv₂ erreicht seinen größten Werth, wenn sich
beide Einflüsse summiren, und wir erhalten Δv₂ = ∓ (Δnv₂ n + Δnn₂)/n²
oder, wenn wir Zähler und Nenner durch n dividiren, Δv₂
= ∓ 0,1 v₂/n. In analoger Weise erhalten wir für
Δv'₂ = ± 0,1
v'₂/n und ΔK = 216 (v'₂² + v₂²/n) 0,1. Führt man n wie oben
in beiden Fällen mit 80 ein, so ergibt sich ΔK = 0,27 (v'₂² + v₂²).
Nimmt man als kleinstes, praktisch brauchbares Verhältniß v₂ = 0,25 an, wobei das Bändchen
noch eine solche Spannung aufweist, daß die Wellen sehr deutlich
ausfallen, wovon man sich leicht durch Versuche überzeugt, und
berechnet das Verhältniß v x, welches für die größte im
Bauwesen vorkommende Spannung auftritt, indem man als
Maximalinanspruchnahme 10k für 1qmm in
Rechnung zieht, so ist nach Formel (α) : 10 = 108 (v x² – 0,0625),
daraus v x = 0,394, und man erhält
hiernach für ΔK = 0k,058 auf 1qmm oder 0,58 Proc. des
Werthes. Setzt man als Grenzwerth für die Abschätzung nicht 0mm,1, sondern 0mm,5, so nimmt der Ausdruck
das 5fache des Werthes an, und man erhält als Fehler 3 Proc. des
Werthes.Die
Differenz der bei der Constantenbestimmung erhaltenen Resultate
findet ihre Ursache in erster Linie wohl nicht in der
Unsicherheit der Ablesung der einzelnen Schwingungszahlen, als
vielmehr in dem Umstande, daß eine Drehung der
Mikrometerschraube um eine volle Windung sich am benutzten
Apparate nicht mit der nöthigen Präcision ausführen ließ. Diesem
Uebelstande soll bei einem künftigen Instrumente abgeholfen
werden, indem es an den Mikrometerschrauben in Grade getheilte
Köpfe mit Ablesemarken erhalten soll.
Um die oben angegebene Fehlergrenze von 0k,058 durch directe Messung
der Längenänderung des Stabes von 400mm Länge zu finden, müßte
man diese Messung bis auf 0mm,001 genau anstellen. Der Apparat ersetzt also hier
gewissermaßen einen Fühlhebel von 100facher Vergrößerung, bei
dessen Ablesung 0mm,1
als Fehlergrenze angenommen wird. Aus dem Ausdrucke für den
Fehler sieht man ferner, daß die Genauigkeit um so größer wird,
je größer man n nimmt und je kleiner
v₁ und v₂ ausfallen, je tiefer also der Ton ist. Man wird
daher starke Spannungen möglichst vermeiden.
Bei eintretender Biegung werden die Bändchen oft größere
Inanspruchnahme erfahren als der Stab selbst. Bei dem größten
Werth, den v überhaupt annehmen
kann, soll die Elasticitätsgrenze des Materials der Bändchen
nicht überschritten werden.
Wenn man für die Beanspruchung an der Elasticitätsgrenze 60k auf 1qmm annimmt, so ist nach
Formel (α) 60 = 108 v'₂² max und v'₂² = 0,5555, v = 0,746. Für diesen Werth wird der
äquivalente Werth für den Fehler bei directer Längenmessung etwa
0mm,003, wobei v₁ = 0,25 gesetzt wurde. Durch
Rückschluß auf diesen Fehler ist es auch leicht, nach Formel l/r = (Δl₂ – Δl₁)/(a₂ – a₁) Anhaltspunkte für die Größe
des bei Ermittlung des Krümmungsmaßes auftretenden Fehlers im
einzelnen Falle zu gewinnen.
Praktische
Durchführung. Zum Zwecke der nähern Beschreibung der
Durchführung mögen hier noch einige Bemerkungen Platz
finden.
Der Transport des Instrumentes erfolgt am
leichtesten mit Hilfe eines Bretchens, das mittels Schrauben an
die Klammern befestigt wird und in der Zeichnung weggelassen
wurde. Man kann dann die Bändchen stets befestigt erhalten und
hat immer die Entfernung der Klammern fixirt.
Das Anbringen des Apparates an dem zu
untersuchenden Stabe hat mit einiger Vorsicht zu geschehen; vor
Allem ist daraus zu achten, daß die glatten Flächen der Backen
gut anliegen; durch allfälliges Glattfeilen der Unebenheiten des
Stabes kann nachgeholfen werden. Im Weitern ist bei gelüfteten
Schrauben, mittels denen die Klammern am Transportbretchen
befestigt sind, eine Klammer durch Anziehen von S festzustellen und nun die zweite
Klammer in die richtige Entfernung l
zu bringen und parallel zu stellen. Ist dies geschehen, wird
auch die zweite Schraube S
angezogen. Diese ganze Manipulation hat bei schlaffen Bändchen
zu geschehen.
Durch Anziehen der Stifte s werden nun die Klammern vollends
fixirt, dann die Bändchen durch Drehen der Mikrometerschrauben
gespannt, bis jedes derselben einen hellen Ton gibt. Wie weit
man hierin gehen darf, muß die Uebung zeigen. Tritt im zu
untersuchenden Stabe voraussichtlich Druck ein, so wird man die
Anspannung schärfer, also den Ton höher, im entgegengesetzten
Falle tiefer machen. Es ist keineswegs nothwendig, jedoch
nützlich, beide Bändchen dem Gehöre nach auf den gleichen Ton zu
bringen.
Nun wird, wie oben erklärt, ein berußtes
Glasplättchen in den Schlitten gesteckt, derselbe nach rechts
geschoben, die berußte Fläche gegen die Federchen bis zur
leichten Berührung gebracht. Liegt eines derselben
nicht gut an, so kann durch eine mittels des Fingers zu
bewirkende, kleine Biegung desselben leicht nachgeholfen werden.
Hierauf wird der Keil zwischen die Zacken der Stimmgabel und die
gespannten Bündchen gesteckt, wodurch zugleich der Schlitten
Widerhalt findet. Der Keil ist so eingerichtet, daß die
Entfernung seiner Theile geändert werden kann, damit stets ein
gleichmäßiges Anspannen beider Bändchen, deren Entfernung von
den Zacken der Stimmgabel sich ändert, wenn die
Keilflanschenfläche nicht stets ganz parallel zu den Bändchen
aufsitzt, möglich sei.
Soll der Versuch gemacht werden, so braucht
man nur den Keil mittels der daran hängenden Schnur rasch
herauszuziehen. Ist letztere hinreichend lang, so ist der Platz,
an dem man sich zu diesem Ende aufzustellen braucht, ziemlich
gleichgiltig – ein Umstand, der namentlich bei Versuchen
an Brücken während des Darüberfahrens von Zügen nicht werthlos
sein dürfte. Ist das Phonogramm verzeichnet, entfernt man durch
Niederdrücken des Hebels den Rahmen mit dem Schlitten von den
Federchen und zieht das Plättchen heraus.
Zum Aufbewahren der Platten kann man sich
eines kleinen, mit Coulissen versehenen Kästchens bedienen, das
zugleich stets den nöthigen Vorrath an berußten Gläsern enthält.
An Stelle der Glasplättchen ist auch feines Papier, das
entsprechend versteift ist, benutzbar. Das Berußen geschieht am
einfachsten, indem man die Platte über eine freie Oel- oder
Kerzenflamme hält und mehrmals hin und her bewegt. Es ist nicht
nöthig, den Ruß sehr dick aufzutragen; die Curven fallen im
Gegentheile auf leicht berußten Flächen schärfer und feiner aus.
Papier wird vor dem Berußen schwach mit Wasser befeuchtet.
Um die Phonogramme zu fixiren, läßt man
Collodium oder einen schnell trocknenden Firniß, dessen sich die
Photographen bedienen, über das Plättchen fließen. Ist es
trocken, so kann man mittels eines Stahlstiftes auf der berußten
Fläche wie mit Bleistift auf einer Papierfläche zeichnen.
Bestimmung von v.
Wichtig ist die genaue Abzählung der in gleichen Zeiten
gemachten Schwingungen. Die ersteren Schwingungen sind hierzu
unbrauchbar, da sie der geringen Anfangsgeschwindigkeit des
Plättchens wegen zu nahe an einander liegen. Nach Erfahrungen,
die ich hierüber gewonnen, geht man wohl am besten, wie folgt,
vor: Man markirt sich mit Zuhilfenahme der Loupe die höchste
Spitze des letzten Wellenberges I
(Fig. 38)
der Bändchenschwingung, die vollkommen scharf erkennbar
erscheint, und zählt nur eine Anzahl von Wellenbergen ab, die
vollkommen deutlich erscheinen; ihre Zahl sei m₁. Dadurch, daß das Plättchen
zur Ruhe kommt, noch ehe die Schwingungen aufgehört haben,
markirt sich der Endpunkt der Schwingungscurve ganz genau als
kleiner verticaler Strich O. Die
Striche O der drei Curven würden
genau über einander stehen, wenn die Spitzen der Federchen genau
in einer Verticalen stünden, was praktisch kaum erreichbar ist,
aber bedeutungslos wird, wenn man die Strecke OI auch vom Punkte O der Stimmgabelcurve aus aufträgt;
ebenso nimmt man den Abstand des Punktes O vom ersten der markirten Wellenberge I' aus und trägt ihn von O der Stimmgabelcurve aus auf. Zählt man
nun die Zahl m der Wellenlängen der
Stimmgabelcurve, die zwischen I und
I' liegen, ab, wobei man Zehntel
derselben noch abschätzen kann, so gibt m₁/m das Verhältniß der
Schwingungszahlen zweier in gleichen Zeiten beschriebenen
Curven, also v₁.
Sind die Federchen nicht in der Mitte der
Bändchen befestigt, so zeigen die Curven nicht reine
Sinuslinien, sondern eigenthümliche secundäre Berge und Thäler,
die zwischen den Maxima und Minima liegen. Sie rühren neben
anderem von dem Umstande her, daß die Bändchen nicht nur als
Ganzes, sondern auch in Theilen schwingen, d.h. Obertöne
entstehen. Auf die Bestimmung der Hauptschwingungszahl, die hier
allein in Betracht kommt, ist dies ohne Einfluß.
Ich wählte Bändchen, an Stelle von
ursprünglich projectirten schwingenden Saiten, weil diese
während des Schwingens keine seitlichen Oscillationen machen,
daher die Phonogramme viel genauer ausfallen.
Vortheile der
Anwendung. Die Anwendung des vorbeschriebenen Apparates
dürfte eine Reihe von Vortheilen mit sich bringen, die im
Nachstehenden kurz beleuchtet werden sollen.
1) Da der Apparat bei geringer Modification
der Klemmschraube sich an beliebigen Stellen einer beanspruchten
Construction anschrauben läßt, ist man im Stande, örtlich
auftretende Spannungen zu messen. Man vermag z.B. leicht zu
untersuchen, in welcher Weise sich die Spannung des Gurtes auf
die Decklamellen und die Stehbleche vertheilt, wie die
Spannungen der Gitterstäbe an den Befestigungsstellen sich
verhalten etc. Welche große Vortheile die Theorie der Brücken
aus solchen Versuchen schöpfen kann, braucht wohl nicht näher
beleuchtet zu werden.
2) Da die ganze Manipulation während der
Beanspruchung nur darin besteht, den Keil herauszuziehen, kann
man die Versuche vornehmen, während Züge die zu prüfende Brücke
passiren, und ist dadurch im Stande, den Einfluß der
Geschwindigkeit und Stöße auf die Beanspruchung zu
constatiren.
3) In den berußten Plättchen, deren
Phonogramme fixirt sind, besitzt man Documente, die jederzeit
über den gemachten Versuch Rechenschaft geben. Die Ermittlung
der Beanspruchung aus den Phonogrammen kann in aller Ruhe zu
Hause geschehen und jederzeit controlirt werden, was namentlich
für die staatliche Inspection von Werth ist.
4) Bei der Montirung wird sich die Verwendung
empfehlen, um zu constatiren, ob sich die Spannungen zu gleichen
Theilen auf einzelne Constructionsglieder, die hierfür berechnet
sind, übertragen; so z.B. auf die Glieder einer Kettenbrücke,
eines gezogenen Gurtes etc.
5) Von großem Werthe dürfte es sein, daß uns
der Apparat in den Stand setzt, die geringste Biegung und den
Sinn derselben an einzelnen Constructionstheilen sofort zu
constatiren. Es wäre dies namentlich bei allen Versuchen, die
mit Knickfestigkeit im Zusammenhange stehen, von Bedeutung.
6) Auch den Versuchsanstalten über
Baumaterialien dürfte vielleicht manches Nützliche aus den
angegebenen Principien erwachsen, um Beanspruchung und Biegung
zu messen etc. Die Nachtheile, die dem Apparate anhaften, sind
wohl vor allem die, daß man bei ausgeführten Brücken nur die
relative, durch die zufällige Belastung hervorgerufene
Beanspruchung messen kann, und daß die Federchen etwas
empfindlicher Natur sind, daher besonders sorgfältig behandelt
werden müssen. Der erstere Nachtheil ließe sich allerdings
dadurch einigermaßen beseitigen, daß man den Einfluß des
Eigengewichtes in indirecter Weise erprobt, indem man auf die
Construction eine gleichmäßig vertheilte, ruhende Belastung
bringt, die einen bekannten Theil des Eigengewichtes ausmacht,
und aus den Beanspruchungen welche sich hierbei ergeben, auf die
durch das Eigengewicht hervorgerufenen schließt. Ein weiterer
Nachtheil, den die Methode mit allen ähnlichen theilt, die
direct oder indirect auf die Messung der Längenänderung
hinauslaufen, liegt in dem Umstande, daß in der Formel für die
Inanspruchnahme der Elasticitätscoefficient des Versuchsstückes
erscheint, mithin das Resultat nur bis auf jene Grenzen
verläßlich sein kann, innerhalb welcher letztere Erfahrungsgröße
liegt. Dasselbe ist aber auch bei dem Verfahren Göbbel's, Dupuy's, sowie beim Messen der
Durchbiegung der Fall. Ob und welche Uebelstände noch in der
Methode liegen, muß die Erfahrung lehren.
Tafeln