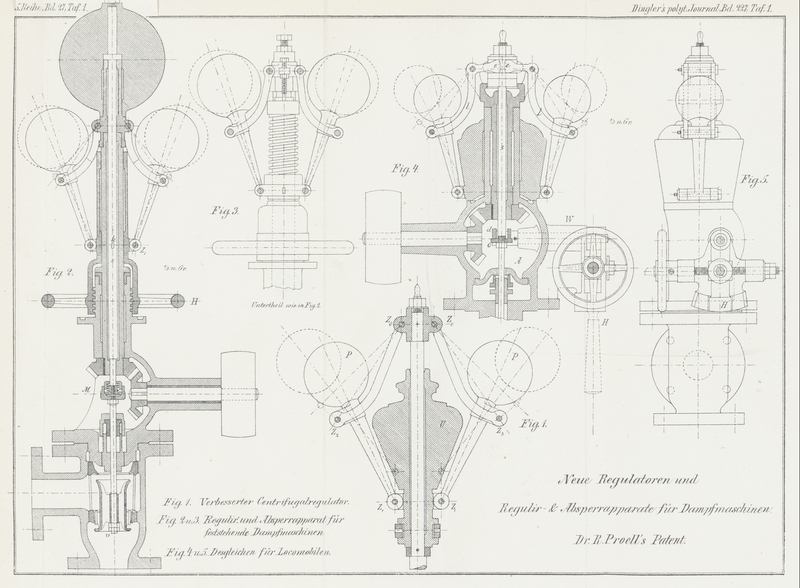
| Titel: | Ueber neue Regulatoren und vollständige Regulir- und Absperrapparate für Dampfmaschinen. Dr. Pröll's Patent. |
| Autor: | R. |
| Fundstelle: | Band 227, Jahrgang 1878, S. 113 |
| Download: | XML |
Ueber neue Regulatoren und vollständige Regulir-
und Absperrapparate für Dampfmaschinen. Dr. Pröll's Patent.
Mit Abbildungen im Text und auf Tafel 1.
(Schluss von S. 16 dieses Bandes.)
Ueber Pröll's Regulatoren.
D) Zur Theorie der Pröll'schen Regulatoren. Man kann von
den Regulatoren in theoretischer Beziehung folgendes verlangen:
1) eine entsprechend grosse Beweglichkeit innerhalb eines
bestimmten Ausschlages.
2) die Entwicklung einer dem Widerstände in der
Regulirungsvorrichtung entsprechenden Energie bei geringer
Tourenänderung.
3) Die relativ geringste räumliche Ausdehnung bei
grösstmöglichenn Arbeitsvermögen.
4) Eine derartige Wahl zwischen Kugel- und Belastungsgewicht,
dass die schädliche Einwirkung der Trägheit ein Minimum werde.
Die Erfüllung dieser Forderungen ist allgemeiner Natur. Wir werden daher so weit als
thunlich aus den weiterhin gefolgerten Resultaten auch den Cosinusregulator auf
seine angebliche Ueberlegenheit verwandten Constructionen gegenüber prüfen.
1) Die Beweglichkeit eines Centrifugalregulators ist
offenbar um so grösser, je mehr sich derselbe der Astasie nähert. Während die
astatische Curve, d. h, diejenige Curve, in welcher sich der Kugel-Mittelpunkt
bewegen müsste, wenn bei einer constanten unveränderlichen Geschwindigkeit der
Regulator in jeder Lage sich im Gleichgewicht befände, rechnerisch leicht aus dem im
Mechanismus des Regulators wirkenden Kräften hergeleitet werden kann, ist das
vortheilhafteste Mass der Annäherung an die Astasie durch die Praxis
festgestellt.
Die vorhin unter A beschriebene eigenthümliche zwangläufige Führung der Kugel bringt
es mit sich, dass bei den in der Ausführung gewählten Dimensionen die Bahncurve des Kugelmittelpunktes im Betrage des durch
die Praxis vorgeschriebenen Ungleichförmigkeitsgrades von etwa 2 Proc. von der
astatischen Curve abweicht.
Bei der Berechnung der Regulatoren, wurde aus der angenommenen Führung des
Kugelträgers, dessen Dimensionen und einem aus der angenommenen mittlern Tourenzahl bestimmten
Verhältniss von Kugelgewicht, dividirt durch Belastungsgewicht, rückwärts auf
graphodynamischem Wege und mittels einer besonders hierzu berechneten Tabelle die
Tourenzahlen n für verschiedene Lagen des Regulators
ermittelt und aus dem Anwachsen derselben ein Schluss auf die zweckentsprechende
Abweichung der Bahncurve des Kugelmittelpunktes von der astatischen Curve
festgestellt. Diese Untersuchung wurde sowohl für eine constante als variable
Belastung des Regulators angestellt. Durch eine besondere Correcturrechnung wurde
schliesslich noch der Einfluss der Gelenkverbindung auf die Wirkungsweise des
Regulators bestimmt – eine Rechnung, die nothwendig war, da bei Bestimmung des
Gleichgewichtszustandes die Einwirkung der in den Massentheilchen der
Gelenkverbindung auftretenden Schwer- und Centrifugalkräfte vernachlässigt
wurde.
Nach Darlegung des Ganges der Berechnung sollen nun im Folgenden die wichtigsten
Gleichungen und Constructionen, mit denen dieselbe geführt wurde, hergeleitet
werden. Wenn man sich vorstellt, dass sich der Regulator in Fig. 6 in Umdrehung befindet, so treten an demselben
drei Kräfte in Wechselwirkung und zwar:
P die Schwere der Schwungkugeln,
C die in denselben auftretende Centrifugalkraft,
2 G die Schwere des Belastungsgewichtes bez. Spannung
der Feder.
Fig. 6., Bd. 237, S. 114
Man findet bekanntlich das Gleichgewicht dieser Kräfte durch Ansetzen der
Momentengleichung in Bezug auf den Pol \frakfamily{P}
(Momentancentrum). Es wird hierbei nur die Hälfte des Regulators in Betracht
gezogen.
Mit Berücksichtigung der in Fig. 6
eingeschriebenen Bezeichnungen ist Gb=Cc-Pp, ferner
C=\frac{P}{g}\,\omega^2r worin ω
die Winkelgeschwindigkeit um die Regulatorachse, g die
Beschleunigung der Schwere bedeutet. Demnach folgt:
Gb=P\left(\frac{\omega^2rc}{g}-p\right), also
\frac{Gb}{P}+p=\frac{\omega^2rc}{g} oder
\frac{r}{\frac{g}{\omega^2}}=\frac{\frac{Gb}{P}+p}{c}.
Aus dieser Gleichung kann folgende geometrische Construction
des Werthes
\left(\frac{g}{\omega^2}\right) gefolgert werden: Man ziehe durch
den Pol \frakfamily{P} eine Verticale und mache auf derselben
\frakfamily{P}E=P, ferner auf der Horizontalen durch
\frakfamily{P} Strecke \frakfamily{P}H=G
und verbinde EH. Dann drehe man die Strecke
\frakfamily{P}C=b um \frakfamily{P} in die
Verticale, so dass \frakfamily{P}K=b ist, ziehe durch K eine Parallele zu EH,
welche auf der Horizontalen durch \frakfamily{P} den Punkt L bestimmt. Der durch L
und den Kugelmittelpunkt D gezogene Strahl gibt die
Richtung der Resultante aus Centrifugalkraft und Schwere der Kugel und schneidet auf
der Regulatorachse oberhalb der Horizontalen durch D
eine Strecke OS=\frac{g}{\omega^2} ab. Der Beweis für die
Richtigkeit der Construction folgt sehr leicht aus der Aehnlichkeit der Dreiecke OSD und DVL.
Auf Grund dieser ausserordentlich bequemen geometrischen Construction des
WerthesDie graphische Construction des Werthes \frac{g}{\omega^2}
ist unabhängig von dem Gesetz, nach welchem sich das Belastungsgewicht 2G mit dem Hube ändert. Sie bleibt also
dieselbe, ob 2G constant oder variabel ist. Im
letztern Falle kann die Variabilität nach irgend einem Gesetze gegeben
sein.
\frac{g}{\omega^2} ist für den Regulator III der Lauchhammer'schen Scale die Tabelle (a. f. S.)
bestimmt. Der Hub des Regulators III von 60mm
wurde in vier gleiche Theile getheilt und die fünf Theilpunkte numerirt.
Aus umstehender Tabelle folgt der Unbeweglichkeitsgrad
\xi=\frac{90,8-89,5}{90}=\frac{1,3}{90}=0,0144.
Die Gelenkverbindung macht nach den Correcturrechnungen, die
wir wegen ihrer Weitläufigkeit hier nicht mittheilen können, den Regulator ein wenig statischer,
so dass sich der Unbeweglichkeitsgrad auf ξ auf rund
0,02 stellen dürfte.
Lage
1
2
3
4
5
Gemessen
\frac{g}{\omega^2}
111
110,5
110
109
107,5
in Millimeter
n
89,50
89,75
90,00
90,30
90,80
Touren in 1 Min.
H
196
194
191
186
182
in Millimeter
E
1,53
1,515
1,50
1,48
1,46
in Kilogr. bez. auf1/50 Tourenänderung
Die Werthe n sind aus
\frac{g}{\omega^2} mit Hilfe der von Dr. Pröll im Civilinqenieur,
1876 Bd. 22 S. 270 berechneten Tabelle bestimmt. Die Bedeutung der Werthe h und E folgt später.
2) Was die Energie des Pröll'schen Regulators anbelangt,
so ist zu erwähnen, dass dieselbe ebenfalls auf graphischem Wege auf Grund folgender Construction ermittelt wurde.
Wenn die Winkelgeschwindigkeit der Regulatorspindel auf ω1 steigt, so erhält der Regulator das
Bestreben, seine Lage zu verändern. Er wird daran durch eine Mehrbelastung 2K der Hülse behindert, die aequivalent der Energie E
des Regulators ist. Aus der Gleichgewichtsgleichung
Gb+Pp=\frac{P}{g}\,\omega^2rc folgt
\frac{\omega^2}{g}=\frac{p}{rc}+\frac{G}{P}\frac{b}{rc} also
auch
\frac{{\omega_1}^2}{g}=\frac{p}{rc}+\frac{G+K}{P}\frac{b}{rc}.
Beide Gleichungen von einander subtrahirt gibt:
\frac{{\omega_1}^2-\omega^2}{g}=\frac{Kb}{Prc}, woraus
K=\frac{rc}{b}\,\frac{{\omega_1}^2-\omega^2}{g}\,P. Es kann
der Werth \frac{rc}{b} als graphische Grösse der Zeichnung Fig. 6 entnommen werden.
Wenn man nämlich durch den Kugelmittelpunkt D eine
Horizontale bezieh. Verticale legt und vom Pol \frakfamily{P}
Strecke \frakfamily{P}J=MC=a macht und JS zieht, so ist die durch diese Linie auf der Verticalen durch D abgeschnittene Strecke
DN=\frac{rc}{b}. Bezeichnen wir dieselbe mit h so folgt \frac{h}{r}=tang\
\delta=\frac{c}{b}, also h=\frac{rc}{b}. Die
Gleichung für die Energie lautet demnach
E=2\,hP\left(\frac{{\omega_1}^2-\omega^2}{g}\right).
Dividiren wir beide Seiten der Gleichung durch
\frac{2\omega^2}{g}, so folgt
\frac{E}{\frac{2\,\omega^2}{g}}=2\,hP\left(\frac{{\omega_1}^2-\omega^2}{2\,\omega^2}\right).
Bekanntlich ist
\frac{{\omega_1}^2-\omega^2}{2\,\omega^2}=\varepsilon dem
Unempfindlichkeitsgrad. Setzen wir diesen Werth ein, so können wir aus der
erhaltenen Gleichung
\frac{Eg}{\omega^2}=4\,hP\varepsilon die Proportion bilden
E:h=4\,P\varepsilon:\frac{g}{\omega^2}. Der Werth
\frac{g}{\omega^2} ist als geometrische Strecke SO gefunden, ε = 1/50 wird angenommen, P und h sind bekannt,
somit folgt graphisch E.
Wenn wir somit in Fig. 6 auf der
Regulatorachse von O die Strecke OT = 4Pε auftragen, die
Strahlen LO und JS in U zum Schnitt bringen und UT ziehen, so schneidet die Richtung von UT
auf der Schwerrichtung des Kugelmittelpunktes die Strecke DW = E ab, also die Energie des Regulators,
gemessen in dem Massstabe, in welchem OT = 4 Pε aufgetragen wurde.
Wiederholt man diese graphische Construction der Energie
für die in obiger Tabelle angenommenen fünf Lagen des Regulators, so bestimmen die
fünf Punkte W eine Curve, deren verticale Abstände von der
Bahncurve des Kugelmittelpunktes proportional der Energie sind. Genaue
graphische Aufzeichnungen dieser Curve haben gezeigt, dass diese fast ganz die um eine constante Strecke abwärts gerückte Bahncurve ist, mit andern Worten, dass
die Energie des Pröll'schen Regulators fast ganz
constant ist, jedenfalls bedeutend constanter als bei dem Cosinusregulator,
bei welchem die Veränderlichkeit der Energie innerhalb des verwendeten Ausschlages
etwa 10 Proc. beträgt. Dies zeigt auch die Tabelle, welche die den 5 Theilpunkten
entsprechenden und nach den angegebenen Constructionen ermittelten Werthe von h und E enthält. Hiernach
beträgt die Energie des Pröll'schen Regulators Nr. III in mittlerer Lage 1k,5 bezogen auf 1/30 Tourenänderung. Die Veränderlichkeit
in der Energie ergibt sich aus den Grenzlagen, indem wir den Quotienten
\frac{1,53-1,46}{1,50}=0,046 bilden. Sie beträgt also nur 4,6
Proc.
3) Die dritte Forderung der Praxis dürfte bei den Pröll'schen Regulatoren ebenfalls
erfüllt sein. Die Wirkung der Kräfte ist unabhängig von der Art und Weise, wie der
Kugelmittelpunkt gezwungen wird, sich in einer geeigneten Bahn zu bewegen. Die
Schwungkugel gehört einem zwangläufig geführten System an. Auch bei dem
Cosinusregulator ist dies der Fall. Während sich bei dem Pröll'schen Regulator der
Kugelmittelpunkt, der nahezu mit dem Schwerpunkt des Kugelträgers zusammenfällt, in
einer Curve höheren Grades bewegt, wird der Schwerpunkt des Pendels im
Cosinusregulator in einer Ellipse geführt. Heide Regulatoren bilden somit eine
besondere Klasse denjenigen Regulatoren gegenüber, bei welchen der Kugelmittelpunkt
(bezieh. Schwerpunkt des Pendels) in einer Kreisbahn geführt wird.
Die Untersuchung, bei welchem der beiden hier gegenüber gestellten Regulatoren die
zur Herbeiführung grosser Beweglichkeit und grossen Arbeitsvermögens (Energie) bei
geringster räumlicher Ausdehnung aufgewendeten Mittel die einfachsten und
zweckentsprechendsten sind, dürfte wohl nur zu Gunsten des Pröll'schen Regulators
ausfallen.
4) Die Erfüllung der vierten Forderung ist in scharfer Weise durch Rechnung kaum zu
bewerkstelligen, da die Verhältnisse zu verwickelt sind. In der Praxis beseitigt man
den schädlichen Einfluss der Trägheit durch Verbindung des Regulators mit einer
Oelbremse (Katarakt). Dieselbe ist vom Standpunkt der Theorie aus sogar geboten, wie
in einem im Civilingenieur, 1877 S. 95 ff. erschienenen
sehr interessanten Aufsatz von Wischnegradski, betitelt
„Ueber direct wirkende Regulatoren“,
gezeigt wird.
Bei Regulatoren, die indess ohne Oelbremse als Specialartikel in den Handel gebracht
werden, hat dagegen die Frage: ob es nicht möglich ist,
durch geeignete Wahl des Verhältnisses von Kugelgewicht zum Belastungsgewicht
den üblen Einfluss der Trägheit so viel als möglich herabzumindern, eine
gewisse Bedeutung. Folgende elementar geführte Untersuchung dürfte vielleicht
geeignet sein, diese Frage in bestimmter Weise zu beantworten.
Bezeichnen wir in Fig. 6 mit l die Entfernung des Kugelmittelpunktes D vom untern zwangläufig geführten Zapfenmittel C, mit r und r1 die
Geschwindigkeitsradien der Punkte C und D, mit Mündig die in C und
D concentrirt gedachten Massen des halben
Belastungsgewichtes und der Kugel, und reduciren wir die Masse M1, nach M, so ist das polare Trägheitsmoment der reducirten
Masse \frakfamily{M}, welche äquivalent den beiden Massen M und M1 ist:
\frakfamily{M}r^2=Mr^2+M_1\,{r_1}^2, woraus
\frakfamily{M}=M+M_1\,\left(\frac{r_1}{r}\right)^2.
Wenn die Geschwindigkeit ω den unendlich kleinen Zuwachs
dω erhält, so tritt in der Hülse die Energie
E=2\,K auf oder für die eine Hälfte des Regulators die
Energie K. Während die Regulatorhülse den Weg ds zurücklegt, nimmt K bis
Null ab, also ist angenähert die eine Ansammlung von lebendiger Kraft im Kugelträger
verursachende Elementararbeit =K\,\frac{ds}{2}. Die lebendige
Kraft der reducirten Masse \frakfamily{M} ist
\frac{\frakfamily{M}v^2}{2}, daher muss sein
\frac{\frakfamily{M}v^2}{2}=\frac{Kds}{2}, also
\frakfamily{M}v^2=Kds. Es bedeutet v die Tangentialgeschwindigkeit in der Bahncurve des
Kugelmittelpunktes.
Wir hatten vorhin berechnet:
\frakfamily{M}=M+M_1\left(\frac{r_1}{r}\right)^2, somit
folgt:
\left[M+M_1\left(\frac{r_1}{r}\right)^2\right]v^2=Kds, also
r=\sqrt{\frac{Kds}{M+M_1\left(\frac{r_1}{r}\right)^2}}.
Die während einer unendlich kleinen Verschiebung des Systems statthabende Bewegung
ist eine harmonische. Die Zeit, welche vergeht, bis das Zapfenmittel C (Fig. 6)
den unendlich kleinen Weg ds zurückgelegt hat, ist
hiernach t_1=\frac{\pi}{2}\frac{ds}{v}. Sehen wir für den
Augenblick von allen Reibungswiderständen in den Gelenkverbindungen und im Stellzeug
ab, so wird der Punkt C in Folge der auftretenden
Energie K eine volle Schwingung vollführen. Der Weg
dieser Schwingung ist 2ds und die Zeit, welche vergeht,
ehe der Punkt C wieder in seine ursprüngliche Lage
kommt, ist t=\frac{2\pi ds}{v}. Diejenigen Gewichtsverhältnisse werden die günstigsten sein, für welche der
Werth t ein Minimum wird. Setzen wir den Werth für v ein, so folgt:
t=\frac{2\pi
ds}{\sqrt{\frac{Kds}{M+M_1\left(\frac{r_1}{r}\right)^2}}} oder
t=2\pi
\,\sqrt{\frac{M+M_1\left(\frac{r_1}{r}\right)^2}{K}}\,\sqrt{ds}
Nun ist die unter (2) hergeleitete Gleichung für die Energie
K=\frac{2\,P}{g}h\,({\omega_1}^2-\omega^2);
ω hatte den Zuwachs dω erhalten, daher folgt
\omega_1=\omega+d\omega, also
{\omega_1}^2=\omega^2+2\,\omega\,d\omega+(d\omega)^2 Das
letzte Glied vernachlässigen wir als ein unendlich kleines Glied zweiter Ordnung. Es
folgt somit {\omega_1}^2-\omega^2=2\,\omega\,d\omega, somit
K=\frac{4\,P}{g}\,h\omega\,d\omega=4\,M_1\,h\omega\,d\omega.
Die Gleichung für t geht somit über in
t=2\pi\sqrt{\frac{M+M_1\left(\frac{r_1}{r}\right)^2}{4\,M_1\,h\omega\,d\omega}}\,\sqrt{ds}=\pi\sqrt{\frac{M+M_1\left(\frac{r_1}{r}\right)^2}{M_1\,\omega
h}}\,\sqrt{\frac{ds}{d\omega}}.
Diese Gleichung ist nun einer interessanten Discussion fähig. Je astatischer ein
Regulator ist, desto mehr nähert sich \sqrt{\frac{ds}{d\omega}}
dem Werthe = ∞; denn bei einem vollkommen astatischen Regulator würde eine
unendlich kleine Geschwindigkeitsvermehrung bereits einen endlichen Ausschlag
herbeiführen. Der Zähler wäre eine endliche Grosse, der Nenner eine unendlich kleine
Grösse, also \frac{ds}{d\omega}=\infty. Die Schwingungszeit
wächst aber proportional \sqrt{\frac{ds}{d\omega}}, somit folgt,
dass die Zeit des Pendelns bei einem Regulator um so
grösser ausfällt, je astatischer er ist, Dies erklärt die unruhige und
darum unbrauchbare Wirkung der astatischen RegulatorenRegulalatoren in der Praxis (selbstverständlich ohne Verbindung mit der Oelbremse). Die
Reibungswiderstände verbessern indess die Wirkung der asiatischen Regulatoren ganz
bedeutend. So ausserordentlich schlimm, als die Theorie lehrt, steht es darum noch nicht mit den
astatischen Regulatoren. Immerhin verwirft man sie mit Recht in der Praxis. Der
günstige Einfluss der Reibungswiderstände erklärt aber auch andererseits wieder die
Möglichkeit, sich in der Construction der Regulatoren bis auf 2 Proc. der Astasie zu
nähern.
Umgekehrt folgt aus obiger Darstellung, dass je astatischer
ein Regulator ist, desto kleiner \frac{ds}{d\omega}
ausfällt. In dieser Beziehung functioniren daher die statischen Regulatoren
gut.
Man kann das Belastungsgewicht auch durch eine gespannte Feder ersetzen. Da letztere
keine Trägheit besitzt, so lässt sich erwarten, dass ein Vergleich zweier
Regulatoren, die dieselbe Winkelgeschwindigkeit \omega=\omega',
dieselben Dimensionen r, r1, h und dieselben Schwungmassen M1 haben und sich nur
dadurch unterscheiden, dass bei dem Belastungsgewicht 2\,G=2\,Mg
durch eine Feder ersetzt ist, deren Masse gleich Null ist, interessante Resultate
geben wird. Sind t, M1,
ω (M = 0) die Werthe
für einen Regulator I mit Federbelastung, t', M', M1, ω' diejenigen für
einen Regulator II mit Gewichtbelastung, so folgt:
Für Regulator I
t=\pi\sqrt{\frac{M_1\left(\frac{r_1}{r}\right)^2}{M_1\,\omega
h}}\,\sqrt{\frac{ds}{d\omega}}.
„ „ II
t'=\pi\sqrt{\frac{M'_1+M_1\left(\frac{r_1}{r}\right)^2}{M_1\,\omega
h}}\,\sqrt{\frac{ds}{d\omega}}.
Durch Division erhält man
\frac{t'}{t}=\sqrt{\frac{M'r^2+M_1{r_1}^2}{M_1{r_1}^2}}\,\sqrt{\frac{d\omega}{d\omega}}.
Der schädliche Einfluss der Tätigkeit
wird bei demjenigen Regulator am kleinsten sein, bei welchem t den kleinsten
Werth annimmt.
Nun lässt sich aus der hergeleiteten Gleichung für \frac{t'}{t}
erkennen, dass M'r^2+M_1{r_1}^2>M_1{r_1}^2 ist, d.h. der Wegfall der trägen Masse des Belastungsgewichtes
verkleinert die Schwingungszeit t. Aus diesem Grunde functionirt also der
Federregulator besser als der Gewichtsregulator, und unter den letzteren verdient
derjenige den Vorzug, bei welchem der Quotient
X=\frac{M'r^2+M_1{r_1}^2}{M_1r^2\omega h} ein relatives
Minimum wird. Setzen wir \frac{M'}{M_1}=\frac GP, so folgt
X=\left[\frac GP+\left(\frac{r_1}{r}\right)^2\right]\frac{1}{\omega
h}. Führen wir G+P=Q, ein, so folgt
G=Q-P, also X=\left[\left(\frac
QP-1\right)+\left(\frac{r_1}{r}\right)^2\right]\frac1{\omega h}.
Von zwei Regulatoren, bei welchen die Werthe r, r1, ω, h und Q dieselben sind, verdient also derjenige den Vorzug,
bei welchem \frac QP den kleinsten Werth hat.
\frac QP nimmt den kleinsten Werth 1 an, wenn
Q=P, d.h. somit, wenn G+P=P oder
G=0 ist. Je mehr Masse also in den
Kugeln und je weniger Masse in dem Belastungsgewicht concentrirt wird, desto
kleiner wird die Schwingungszeit t. In dieser Beziehung ist es daher
schädlich, ein sehr grosses Verhältniss von \frac QP der
Construction des Regulators zu Grunde zu legen.
Zur Erzielung einer gewissen Energie muss die gesammte schwingende Masse 2 Q des Regulators eine gewisse Grösse erhalten. Dann
kann, da der Werth P durch den für die Schwungkugel
verfügbaren Raum als gegeben zu betrachten ist, ein grösserer Werth von
\frac QP doch nicht umgangen werden.
In der Lauchhammer'schen Scale erhielten darum die
schwächeren Regulatoren den Werth \frac
QP=2,15\,\,\text{bis}\,\,2,6, die stärkeren Regulatoren den Werth
\frac QP=2,9\,\,\text{bis}\,\,4,2.
Vorstehende Untersuchung ist unmittelbar auch auf den Cosinusregulator anwendbar, weil in ihm ebenfalls ein zwangläufig
geführtes Pendel rotirt. Dieser Regulator besitzt eine sehr hohe Tourenzahl und
einen selbst bei schwächeren Nummern relativ grossen Werth von \frac
QP\geq4, während dies bei dem Pröll'schen Regulator nicht der Fall
ist. Die Behauptung, der Cosinusregulator sei der einzig
vollkommene Centrifugalregulator entbehrt daher der wissenschaftlichen
Begründung, abgesehen von andern ihm anhaftenden Unvollkommenheiten, deren
ganze Darlegung uns hier zu weit führen würde.
Weiter folgt, dass d\omega>d\omega' ist, weil die Spannung der
Belastungsfeder mit dem Hube wächst, während dies beim Belastungsgewicht nicht der
Fall ist. Es bedarf also bei dem Federregulator einer grössern
Geschwindigkeitsvermehrung, um ihn zur Hubänderung ds
zu veranlassen, als beim Gewichtsregulator. Also auch aus
diesem Grunde functionirt der Federregulator besser als der
Gewichtsregulator.
Unter Umständen kann es aber zweckmässig erscheinen, um einen möglichst grossen
Beweglichkeitsgrad zu wahren, die Aufhängung für einen Federregulator derartig von
derjenigen eines Gewichtsregulators verschieden zu machen, dass gleichen Werthen ds auch gleiche Werthe dω
entsprechen, also dω = dω' ist. Dann bleibt nur der
vorher begründete Vortheil bestehen, der allein schon recht bedeutend ist.
Wir dürfen nicht unerwähnt lassen, dass die mit Vernachlässigung der Reibung
hergeleitete Gleichung und die aus dieser gezogenen Folgerungen auch sehr angenähert
ihre Bedeutung behalten, wenn wir für ds und dω endliche Werthe Δs und
Δω setzen. Die Gleichung lautet dann
T=\pi\,\sqrt{\frac{M+M_1\left(\frac{r_1}{r}\right)^2}{M_1\omega
h}}\,\sqrt{\frac{\Delta s}{\Delta\omega}}. Endliche Werthe Δs und Δω treten auf, wenn
die Reibung der Ruhe grösser ist als diejenige der Bewegung, was in der Praxis im
Allgemeinen zutreffen dürfte.
Bei dem in Fig.
3 Taf. 1 abgebildeten Regulir- und Absperrapparat für feststehende
Dampfmaschinen ist ein nach vorstehend hergeleiteten Resultaten construirter
Federregulator zur Anwendung gelangt. Die in Lauchhammer stattgehabten VersucheIn der mit dem Eisenwerk Lauchhammer zu
Lauchhammer verbundenen Maschinenfabrik ist eine Versuchsstation errichtet,
in welcher jeder Apparat vor seiner Ablieferung auf seine Leistungsfähigkeit
geprüft wird. haben gezeigt, dass derselbe fast momentan und
schneller den Geschwindigkeitsänderungen der Maschine folgte, als der auf demselben
Apparat befindliche und unter denselben Verhältnissen arbeitende Regulator mit
Kugel- (Gewichts-) Belastung (Fig. 2 Taf. 1), trotzdem
ersterer etwas statischer construirt war als letzterer – ein schöner Beweis für die
Richtigkeit der vorausgeschickten Theorie. Die Regulirapparate mit Federbelastung im
Regulator eignen sich daher vorzüglich für sehr genaue Regulirung.
R.
Tafeln