| Titel: | Ueber die constructiven Erfordernisse und die nöthige Armirung der Saug- und Druckpumpen mit Rücksicht auf deren gehörige Wirkungsfähigkeit; von J. Illeck in Wien. |
| Autor: | J. Illeck |
| Fundstelle: | Band 227, Jahrgang 1878, S. 217 |
| Download: | XML |
Ueber die constructiven Erfordernisse und die
nöthige Armirung der Saug- und Druckpumpen mit Rücksicht auf deren gehörige
Wirkungsfähigkeit; von J. Illeck
in Wien.
Mit Abbildungen auf Tafel
14.
Illeck, über Construction der Saug- und Druckpumpen
Es ist eine ziemlich häufig vorkommende Erscheinung und bekannte Thatsache, dass die
Saug- und Druckpumpen in ihrer Wirksamkeit zeitweilig unverlässlich sind und ihre
Dienste, namentlich bei der Ingangsetzung, oftmals versagen. Die zunächst liegenden
Ursachen solcher manchmal ganz räthselhaft scheinender Störungen können verschiedene
sein, doch lassen sich diese in letzter Reihe stets auf die im Pumpenstiefel und in
der Saugrohrleitung enthaltene oder irgendwie angesammelte Luft zurückführen, welche
diese Räume theilweise oder auch ganz erfüllt und aus denselben selbstthätig durch
das Spiel der Pumpe allein entweder schwer oder gar nicht zu entfernen ist. Es wird
also von Wichtigkeit sein, die in den erwähnten Räumen enthaltene Luft auf
zweckentsprechende Weise vollständig auszutreiben, und hieraus ergibt sich von
selbst ein nahezu unfehlbares Mittel, eine versagende Pumpe zur momentanen Wirkung
zu bringen; man hat nämlich einfach den Pumpenstiefel als auch die Saugrohrleitung
direct mit Wasser zu füllen und der hierbei entweichenden Luft freien Auslass zu
verschaffen; allein diese Methode ist nichts weniger als bequem zu nennen und ist
lange nicht so einfach, als es den Anschein hat.
Empfehlenswerther wird es daher jedenfalls sein, schon bei der Construction der
Pumpen darauf Bedacht zu nehmen, dass deren Ansetzen womöglich mit Luft in allen
Räumen sicher und schnell zu bewerkstelligen ist, zu welchem Ende dieselben nebst
den gehörigen Abmessungen mit einer entsprechenden Armirung zu versehen sind, deren
Angabe und Besprechung an diesem Orte bezweckt wird. Zu bemerken ist hierbei, dass
die erwähnten und in der Folge zu erörternden Hilfsmittel keineswegs originell,
sondern dem Wesentlichen nach wohl mehr oder weniger bekannt sind; allein deren
Kenntniss und Verbreitung ist lange nicht so allgemein, als dass eine
zusammenhängende Darstellung derselben nebst theoretischer Begründung nicht einigen
Nutzen stiften könnte; wenigstens findet man häufig genug Pumpen, denen derlei zwar
unscheinbare, nichts destoweniger aber sehr wichtige Erfordernisse entweder gänzlich
mangeln, oder, wo es leicht ersichtlich ist, dass dieselben erst nachträglich
angebracht werden mussten, und dieser Umstand ist es eben, welcher mir zu der
vorliegenden Arbeit die Anregung gegeben hat.
Zunächst lasse ich einige theoretische Vorbetrachtungen folgen, an welche sich dann
die hierauf gestützten, praktischen Folgerungen anschliessen sollen, und zwar sei
vorerst der einfachste Fall, nämlich
Pumpen ohne oder mit geringer
Saughöhe
einer Betrachtung unterzogen. Es bezeichne für eine einfach
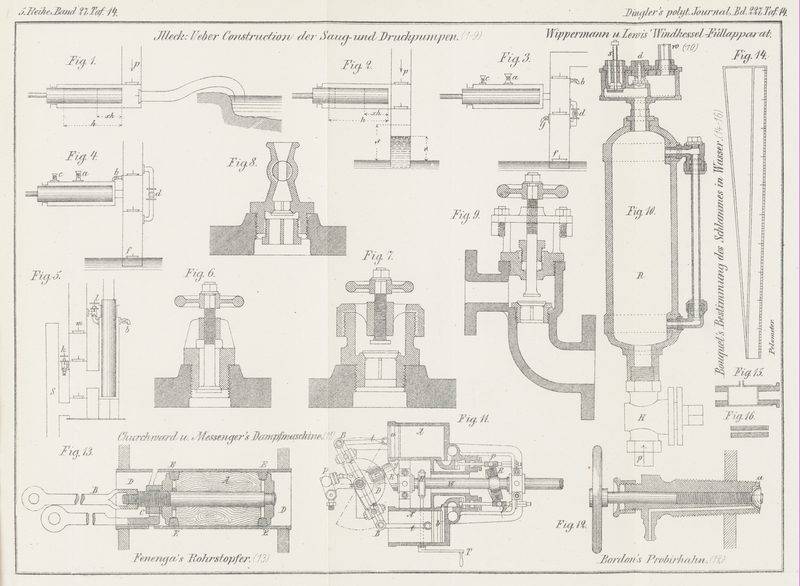
wirkende horizontale Plungerpumpe (Fig. 1 Taf. 14):
v das vom Plunger für jeden Hub beschriebene Volum;
v0 das Volum des
schädlichen Raumes;
V das Volum des Saugrohres;
h den Plungerhub;
p die Druckhöhe der Steigwassersäule (eingeschlossen
Luftdruck);
\frakfamily{H} die Druckhöhe einer Atmosphäre;
k=\frac{v_0}{v} den schädlichen Raum, in Procent des
Plungervolums.
Beim ersten Anhub des Plungers wird das Luftvolum v
angesaugt und beim nächstfolgenden Rücklauf desselben die gesammte Luftmenge
(v+v_0) im Pumpenstiefel auf das Volum v0 comprimirt; die
Compression y ergibt sich aus der Gleichung
\frakfamily{H}\,(v+v_0)=y\,v_0 zu
y=\frac{v+v_0}{v_0}\,\frakfamily{H}=\frac{1+k}{k}\,\frakfamily{H}
. . . . . . . (1)
Findet sich aus Gleichung (1) die Compression y\leqq
p, so kann eine solche Pumpe, wenn die comprimirte Luft nur durch das
Druckventil entweichen kann, gar niemals selbstthätig zur Wirksamkeit gelangen, weil
das fortgesetzte Spiel des Plungers nichts weiter zur Folge hat, als dass die im
Pumpenstiefel eingeschlossene Luft abwechselnd innerhalb derselben Grenzen
comprimirt und expandirt wird, ohne dass die beiden Ventile hierbei jemals zur
Hebung gebracht werden. Setzen wir z.B. k=1, was bei kleinen
Pumpen häufig getroffen wird, so findet sich aus Gleichung (1)
y=2\,\frakfamily{H}; daher
p<2\,\frakfamily{H}; d.h. die Druckhöhe der Pumpe muss
weniger als 2at betragen. Bei grösseren Pumpen
kann k=0,1 gesetzt werden; damit berechnet sich aus Gleichung (1)
y=11\,\frakfamily{H}, folglich
p<11\,\frakfamily{H}. Aus diesem Beispiel ist zu
entnehmen, dass eine Pumpe mit 10 Proc. schädlichem Raume, bei geringer Saughöhe, in
den meisten praktischen Fällen ohne weitere Vorkehrungen selbstthätig zur Wirkung
kommen wird.
Bisher haben wir vorausgesetzt, dass der Pumpenstiefel vollständig mit Luft erfüllt
ist; anders stellt sich der Fall, wenn sich in diesem Raume beim Anlassen der Pumpe
ein Gemenge von Luft und Wasser befindet. Es sei \frakfamily{V}
die genannte Wassermenge und \frakfamily{V}<v_0
angenommen; wenn sich
nun das Druckventil vor Ablauf des Hubes heben soll, so besteht hierfür die
Relation:
\frakfamily{H}\,(v+v_0-\frakfamily{V})>p\,(v_0-\frakfamily{V});
hieraus folgt:
\frac{\frakfamily{V}}{v_0}>1-\frac{\frakfamily{H}}{k\,(p-\frakfamily{H})}
. . . . . . (2)
Diese Gleichung zeigt, dass je nach der Grösse der Wassermenge
\frakfamily{V} im schädlichen Raum jeder beliebig hohe
Ventildruck überwunden werden kann; dieser Umstand wird u.a. bei den sogen. nassen
Luftcompressionspumpen mit Vortheil benutzt. Setzen wir z.B.
k=0,5 und p=5^{at}, so findet sich aus der
letzten Gleichung \frac{\frakfamily{V}}{v_0}>\frac12; d.h. wenn
das Druckventil mit 5at Gegendruck gehoben werden
soll, so muss, k=0,5 vorausgesetzt, mehr als die Hälfte des
schädlichen Raumes mit Wasser gefüllt sein.
Unsere weitere Aufgabe besteht jetzt darin, die Anzahl Touren oder Doppelhübe zu
ermitteln, welche zu machen ist, bis alle Raume vollständig mit Wasser gefüllt sind.
Diese Tourenzahl lässt sich in zwei principiell verschiedene Theile zerlegen, welche
sich auf die Saugrohrleitung einerseits und auf den Inhalt des Pumpenstiefels
andererseits beziehen.
Entfernung der Luft aus der Saugrohrleitung. Hiernach
ist die Tourenzahl n zu bestimmen, bei welcher das
Wasser vom untern Wasserspiegel bis zum Saugventil gelangt. Unter der Voraussetzung,
dass die Compression y>p ist, haben wir uns zu Beginn jedes
Anhubes den schädlichen Raum mit Luft von der Spannung p erfüllt zu denken; sobald der Plunger vorläuft, expandirt die Luft und
erreicht schliesslich die Spannung \frakfamily{H}=1^{at}, wobei
der Plunger den Weg xh (Fig. 1) zurückgelegt haben
soll, in welchem Augenblicke sich das Saugventil zu heben beginnt und von da an
durch den Rest (1-x)\,h des Hubes Luft von der Spannung
\frakfamily{H}=1^{at} angesaugt wird. Die Unbekannte
x<1 findet sich aus der Relation
p\,v_0=\frakfamily{H}\,(v_0+x\,v):
x=k\,\left(\frac{p}{\frakfamily{H}}-1\right). . . . . . . (3)
Die auf jede Tour angesaugte Luftmenge ist hierbei
(1-x)\,v. Demnach wird nach n
Touren zu setzen sein n\,(1-x)\,v=V, woraus die gesuchte
Tourenzahl unter Einsetzung des Werthes x aus Gleichung
(3) folgt:
n=\frac{V}{(1-x)\,v}. . . . . . . (4)
Für k=0, oder auch für
p=\frakfamily{H} ist nach Gleichung (3)
x=0, somit aus Gleichung (4):
n=\frac Vv. . . . . . (5)
Die Gleichung (5) gibt das Minimum der Tourenzahl n an, welches in zwei Fällen
eintritt, wenn die Pumpe keinen schädlichen Raum besitzt und wenn die Belastung des
Druckventiles blos 1at beträgt.
Setzen wir als allgemeines Beispiel: p=5^{at},
k=0,1, V=9\,v, so berechnet sich aus den
Gleichungen (3) und (4) x=0,4 und n=15. Diese
Pumpe muss also 6 Doppelhübe über die Minimalzahl 9 machen, bis das Wasser vom
untern Spiegel bis zum Saugventil vorrückt.
Entfernung der Luft aus dem Pumpenstiefel. Um die Anzahl
m der Doppelhübe zu bestimmen, welche nothwendig
sind, die Luft aus dem Pumpenstiefel zu entfernen, nehmen wir an, dass sich in
letzterem die Luftmenge U<v_0 von der Spannung p befinden soll. Bei einem gewissen Weg xh des Plungers hebt sich das Saugventil, und es tritt
Wasser in den Stiefel ein. Die Unbekannte x findet sich
ähnlich wie früher aus der Relation
p\,U=\frakfamily{H}\,(U+x\,v):
x=\left(\frac{p}{\frakfamily{H}}-1\right)\,\frac Uv. . . . . . .
(6)
Die Gleichung (6) ist mit (3) bis auf den Umstand übereinstimmend, dass dort das
Verhältniss \frac{v_0}{v}=k constant ist, während hier
\frac Uv ein von Tour zu Tour wechselndes Verhältniss
bedeutet.
Im weitern Verlaufe des Hubes wird die Wassermenge (1-x)\,v
angesaugt; hingegen wird beim Rücklaufe des Plungers dem Volum nach dieselbe Menge
comprimirter Luft aus dem Stiefel durch das Druckventil geschafft, und die übrig
bleibende Luftmenge ist demnach: U_1=U-(1-x)\,v, oder mit
Rücksicht auf Gleichung (6):
U_1=\frac{p}{\frakfamily{H}}\,U-v. . . . . . (7)
Mittels dieser Gleichung finden wir nun die von Tour zu Tour
im Pumpenstiefel zurückbleibenden Luftmengen der Reihe nach, Kürze halber
\frac{p}{\frakfamily{H}}=\beta gesetzt:
v_1=\beta v_0-v
nach
der
1.
Tour
v_2=\beta v_1-v
„
„
2.
„
v_3=\beta v_2-v
„
„
3.
„
. . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
v_m=\beta v_{m-1}-v
„
„
m.
„
oder nach gehöriger Substitution:
\begin{array}{rcl}v_1 & = & \beta v_0-v\\v_2 & = & \beta^2
v_0-(1+\beta)\,v\\v_3 & = & \beta^3 v_0-(1+\beta+\beta^2)\,v\\\ldots
&.\,.& \ldots \ldots \ldots \ldots \ldots \ldots \ldots\\v_m & =
& \beta^m v_0-(1+\beta+\beta^2+...+\beta^{m-1})\,v.\end{array}
Nun ist für \beta>1 die Summe der Reihe
1+\beta+\beta^2+...+\beta^{m-1}
=\frac{\beta^m-1}{\beta-1}; daher einfacher
v_m=\beta^mv_0-\frac{\beta^m-1}{\beta-1}\,v oder wegen
\frac{v_0}v=k und
\frac{p}{\frakfamily{H}}=\beta schliesslich:
v_m=\frac{k\left(\frac{p}{\frakfamily{H}}\right)^{m+1}-(k+1)\,\left(\frac{p}{\frakfamily{H}}\right)^m+1}{\frac{p}{\frakfamily{H}}-1}\,v
. . . . . . . (8)
Soll die Luft mit dem m ten Doppelhube aus dem Stiefel
vollständig entfernt sein, so ist hierfür v_m=0 zu setzen, wonach
sich aus (8) die Bedingungsgleichung ergibt:
k\left(\frac{p}{\frakfamily{H}}\right)^{m+1}-(k+1)\,\left(\frac{p}{\frakfamily{H}}\right)^m+1=0
. . . . . . (9)
welche giltig ist, so lange
\frac{p}{\frakfamily{H}}>1 verbleibt. Für
k=0,25 und \frac{p}{\frakfamily{H}}=5
berechnet sich aus Gleichung (9) die gesuchte Tourenzahl m=3.
Für den Fall, dass die Luft mit dem ersten Doppelhube aus dem Stiefel entfernt werden
soll, gilt nach Gleichung (9) mit m=1 die einfachere
Bedingung:
k\left(\frac{p}{\frakfamily{H}}\right)^2-(k+1)\,\frac{p}{\frakfamily{H}}+1=0
. . . . . . (10)
Die eine Wurzel dieser quadratischen Gleichung ist:
\frac{p}{\frakfamily{H}}=\frac 1k . . . . . . (11)
Die Relation (11) drückt also die erforderliche Bedingung aus,
damit die Luft mit einem Doppelhub aus dem Stiefel getrieben wird, welche Bedingung
sich übrigens auch leicht unmittelbar ableiten lässt. Für
k<\frac{p}{\frakfamily{H}} wird nicht nur die ganze
Luft, sondern auch nebst bei Wasser aus dem Stiefel gefördert. Als zweite Wurzel
folgt aus Gleichung (10) \frac{p}{\frakfamily{H}}=1; dieser Werth
ist unbrauchbar, da für denselben Gleichung (9) ihre Giltigkeit verliert; wir müssen
deshalb auf Gleichung (8) zurückgreifen, nach welcher v_m für
p=\frakfamily{H} die Form \frac00
annimmt.
Den wahren Werth von vm
findet man aus Gleichung (8) auf bekannte Weise:
v_m=(k-m)\,v. . . . . . (12)
Setzen wir jetzt wieder v_m=0, so findet
sich aus Gleichung (12) die einfache Bedingung:
m=k, . . . . . . (13)
welche zeigt, dass für k=1 die Luft mit dem
ersten Hube aus dem Stiefel entfernt wird, vorausgesetzt, dass die Belastung des
Druckventiles blos 1at beträgt.
Pumpen, bei welchen die Saughöhe in Betracht zu ziehen
ist. Mit gleichen Argumenten findet man hier ähnliche Resultate, wie
früher, nur sind diese, zum Theile, etwas complicirter herzuleiten, weshalb der
einfachere Fall, Pumpen ohne Saughöhe, vorangeschickt wurde. Es sei in Fig. 2 Taf. 14
H der Abstand des Saugventiles vom untern
Wasserspiegel; im Saugrohr soll das Wasser bereits auf die Höhe z gestiegen sein, und der Plunger befinde sich
gleichzeitig ganz aus dem Stiefel hervorgezogen. In diesem Augenblicke befindet sich
im Plungerstiefel verdünnte Luft von der Spannung
(\frakfamily{H}-z); denken wir uns jetzt den Plunger ganz
vorgeschoben, so wird die eingeschlossene Luft auf die Spannung y verdichtet, welche sich aus der Relation
(\frakfamily{H}-z)\,(v_0+v)=y\,v_0 zu
y=\frac{1+k}{k}\,(\frakfamily{H}-z) gibt. Soll sich also das
Druckventil früher als vor zurückgelegtem Hub erheben, so muss die Druckwassersäule
(eingeschlossen Luftdruck)
p<\frac{1+k}{k}\,(\frakfamily{H}-z) sein. Diese
Beziehung gilt für ein beliebiges z; für den
ungünstigsten Fall z=H findet sich als Relation zwischen der
Saughöhe H und der Druckhöhe p:
\frac{1+k}{k}\,(\frakfamily{H}-H)>p . . . . . . (14)
Für H=\frakfamily{H} folgt daraus
p<0. An die theoretische Saughöhe
H=1^{at} ist also nicht entfernt zu denken; im günstigsten
Falle ist p=\frakfamily{H}, wenn nämlich ein entlastetes
Druckventil beim Anlassen der Pumpe gebraucht wird, oder die Druckhöhe überhaupt
gleich Null ist. Daher muss jedenfalls nach Gleichung (14)
\frac{1+k}{k}\,(\frakfamily{H}-H)>\frakfamily{H} sein, woraus
sich die Maximalsaughöhe zu:
H_{max}<\frac{\frakfamily{H}}{1+k} . . . . . (15)
ergibt, falls die Pumpe zur Wirksamkeit gelangen soll, ohne
dass vorher Stiefel und Saugrohr mit Wasser gefüllt werden müssen. Es berechnet sich
für k=0,1 und k=1 aus Gleichung (15)
H_{max}<0,9\frakfamily{H} bezieh.
H_{max}<0,5\frakfamily{H}. Der letztere Werth wird
besonders für kleinere Pumpen, welche grosse schädliche Räume besitzen und wie
gewöhnlich möglichst hoch ansaugen sollen, zu beachten sein.
Entfernung der Luft aus dem Saugrohr. Um die Anzahl
Touren zu finden, nach welchen das Wasser im Saugrohr bis zum Säugventil steigt,
wollen wir uns, um grösseren Complicationen auszuweichen, mit einer annähernden
Rechnung begnügen. Wir denken uns auch hier wieder den schädlichen Raum v0 der Pumpe mit Luft
von der Spannung p entsprechend der Druckwassersäule
erfüllt; im Saugrohr sei das Wasser auf die Höhe z
(Fig. 2)
gestiegen. Der Plunger wird nun den Weg xh zurücklegen,
bis die Spannung der Luft auf (\frakfamily{H}-z) gefallen ist, in welchem Momente
sich das Saugventil öffnet. Aus der Relation
p\,v_0=(\frakfamily{H}-z)\,(v_0+x\,v) findet sich die
Unbekannte:
x=k\,\left(\frac{p}{\frakfamily{H}-z}-1\right) . . . . . .
(16)
Es soll nun angenommen werden, dass durch den Rest des
Plungerhubes, während der Plunger den Raum (1-x)\,v durchläuft,
die gleiche Wassermenge angesaugt wird, was insofern nicht genau richtig ist, als
durch das Ansteigen des Wassers im Saugrohr die Spannung der Luft im Stiefel unter
(\frakfamily{H}-z) fällt. Unter der gemachten Annahme ist
(1-x)\,v=(z_1-z)\,\frac VH; wobei z1 die Höhe der Wassersäule im Saugrohr am
Ende des Hubes bedeutet. Mit Rücksicht auf Gleichung (16) findet sich nun
allgemein:
z_1=z+\left[1-k\,\left(\frac{p}{\frakfamily{H}-z}-1\right)\right]\,\frac{Hv}{V}
. . . . . . (17)
Die Gleichung (17) erlaubt uns, die Höhe der Wassersäule im Saugrohr von Tour zu Tour
festzustellen; diese Höhen sind:
z_1=\left[1-k\,\left(\frac{p}{\frakfamily{H}}-1\right)\right]\,\frac{Hv}{V}
nach
der
1.
Tour
z_2=z_1+\left[1-k\,\left(\frac{p}{\frakfamily{H}-z_1}-1\right)\right]\,\frac{Hv}{V}
„
„
2.
„
z_n=z_{n-1}+\left[1-k\,\left(\frac{p}{\frakfamily{H}-z_{n-1}}-1\right)\right]\,\frac{Hv}{V}
„
„
n.
„
Man gelangt auf diese Art, allmälig fortschreitend, zur
Kenntniss der Tourenzahl, bei welcher das Wasser bis zum Saugventil gestiegen ist,
da es nicht angeht, dafür in diesem Falle eine directe Formel aufzustellen. Dieser
Weg ist aber in der Regel so langwierig, dass wir uns lieber mit einer weitern
Annäherung begnügen wollen, welche darin besteht, die fraglichen Differenzen der
Wasserspiegel im Saugrohr blos für die äussersten Grenzen zu bestimmen; diese
sind:
z_1=\left[1-k\,\left(\frac{p}{\frakfamily{H}}-1\right)\right]\,\frac{Hv}{V}
zu Beginn des Ansaugens;
z_{n+1}-z_n=\left[1-k\,\left(\frac{p}{\frakfamily{H}-H}-1\right)\right]\,\frac{Hv}{V}
am Ende des Ansaugens.
Setzen wir als Beispiel:
\frac{V}{v}=9,\;H=3^m,\;p=50^m,\;\frakfamily{H}=10^m und
k=0,1, so findet sich z_1=0^m,2, und
z_{n+1}-z_n=0^m,1286. Die mittlere Differenz ist also:
\Delta z=1/2\,(0,2+0,1286)=0^m,1643, und damit berechnet sich
die gesuchte Tourenzahl n annähernd zu
n=\frac{H}{\Delta z}=\frac{3}{0,1643}=18,26. Die fragliche
Tourenzahl erhöht sich also von der Minimalzahl \frac{V}{v}=9 auf
etwa 18, während sie für dasselbe Beispiel, bei der Pumpe ohne Saughöhe, 15
betrug.
Entfernung der Luft aus dem Pumpenstiefel. Die
Berechnung der Tourenzahl m, welche zur Entfernung der
Luft aus dem Pumpenstiefel nöthig ist, stellt sich insofern bedeutend einfacher, als
hierfür die Gleichungen (8) und (9) unverändert giltig bleiben; nur ist in denselben
(\frakfamily{H}-H) statt \frakfamily{H} zu
setzen. Damit findet sich auch hier, unter sonst gleichen Umständen, die Tourenzahl
m erheblich grösser, als bei den Pumpen ohne
Saughöhe.
Mit den obigen Betrachtungen hätten wir das theoretische Material hinreichend
erschöpft und können jetzt, darauf gestützt, auf den Boden der Praxis übergehen.
Praktische Folgerungen. Zunächst theilen wir die Pumpen
in zwei Gruppen ein:
a) In solche, welche nicht selbstthätig, sondern nur dann zur Wirksamkeit gelangen
können, wenn die Räume des Saugrohres und Pumpenstiefels früher vollständig, auf
directem Wege, mit Wasser gefüllt werden. Diese Gattung Pumpen macht sich nach
Gleichung (15) durch die Relation (k+1)\,H\geq\frakfamily{H}
erkenntlich; dieser Bedingung entsprechen beispielsweise die Werthe
H=5^m und k=1.
Solche Pumpen müssen mit folgenden Vorrichtungen ausgerüstet werden, welche in Fig. 3 Taf. 14
angedeutet erscheinen:
1) Eine beliebige Füllvorrichtung a mit Absperrhahn,
welche so beschaffen sein soll, dass die Füllung des Pumpenstiefels mit Wasser
bequem und schnell zu bewerkstelligen ist.
2) Ein Ablasshahn b für die entweichende Luft, welcher
an der obersten Stelle des Pumpenstiefelraumes anzubringen ist. Zuweilen wird für
den gleichen Zweck noch ein zweiter Ablasshahn c, oder
vielleicht, je nach der Constructionsart der Pumpe, werden auch deren mehrere
erforderlich sein.
3) Ein Verbindungsrohr mit Absperrhahn d zwischen dem
Pumpenstiefel und dem Saugrohr, um auch dieses mit Wasser füllen zu können.
4) Ein zweites Saugventil f am Unterende des Saugrohres,
welches dazu dient, die Füllung des letzteren mit Wasser anstandslos durchzuführen;
auch verhindert dieses Ventil, dass die Saugwassersäule bei längerem Stillstande der
Pumpe herabfällt. Für kleine Pumpen, mit enger Saugrohrleitung, kann dieses Ventil
natürlich entfallen; das Wasser zur Füllung muss aber dann in solcher Menge oder so
rasch nachgegossen werden, dass der Querschnitt des Saugrohres vollständig
ausgefüllt wird.
5) Ein Ablasshahn g, welcher an der obersten Stelle des
Saugrohres anzubringen ist, damit die Luft aus letzterem bei der Füllung mit Wasser
entweichen kann. Wenn das Verbindungsrohr d weit genug
ist, so dass dessen Querschnitt von dem zur Füllung bestimmten Wasser nur theilweise
eingenommen wird, dann kann die entweichende Luft auch durch das Rohr d
aufsteigen; der untere Ausgangspunkt des letztern muss aber dann an die oberste
Stelle des Saugrohres verlegt werden. Uebrigens kann dem Ablasshahn g, wie wir später sehen werden, noch eine andere
Function zugewiesen werden.
Für grosse Pumpen mit bedeutender Druckhöhe wird es angezeigt sein, vor der
Ingangsetzung auch die Druckrohrleitung mit Wasser zu füllen, um den
Beharrungszustand der Bewegung und das Gleichgewicht zwischen Kraft und Widerstand
möglichst schnell herbeizuführen. Da man überdies annehmen kann, dass das Druckrohr
für gewöhnlich, mit Ausnahme der ersten Ingangsetzung, stets mit Wasser gefüllt sein
wird, so ist folgende in Fig. 4 Taf. 14 angedeutete
Anordnung im Allgemeinen zweckmässiger und einfacher: Durch das Verbindungsrohr mit
Absperrhahn d wird die Füllung des Saugrohres mit
Wasser von der Druckleitung aus ohne weitere Umstände bequem bewerkstelligt; die
Luft entweicht hierbei durch das obere Saugventil in den Pumpenstiefel und von da
durch den Ablasshahn b ins Freie; sobald dies geschehen
ist, füllt sich auf gleichem Wege auch der Pumpenstiefel mit Wasser, wobei auch der
Hahn c zur vollkommenen Luftentleerung gute Dienste
leistet.
Vorrichtungen zum Abstellen der Pumpen. In den meisten
Fällen ist es nöthig, eine Pumpe bei fortlaufendem Gange der Betriebsmaschine
abstellen zu können. Wird die Pumpe durch eine Transmission angetrieben, so stellt
man sie auf dieselbe Art wie jede andere Arbeitsmaschine ab; andernfalls wird bei
längeren Pausen der Plunger oder Kolben von der Betriebsmaschine ausgekuppelt. Für
kürzere Pausen wäre aber diese Operation, besonders bei grösseren Pumpen, etwas zu
umständlich; man lässt deshalb den Plunger lieber fortlaufen und sorgt auf andere
Weise dafür, dass die Pumpe wirkungslos arbeitet. Bei kleinen Pumpen ist der Plunger
überhaupt selten zum Abstellen eingerichtet und wird letzterer deshalb ohne
Unterbrechung im Gange gelassen.
Um die Wirkung einer Pumpe bei fortlaufendem Gange derselben aufzuheben, kann man
sich verschiedener Mittel bedienen, von denen die am meisten gebräuchlichen folgende
sind:
1) Durch Oeffnung des Hahnes d (Fig. 4), wodurch die
Druckleitung mit der Saugleitung verbunden wird; die Pumpe saugt dann Wasser aus der
Druckleitung durch das obere Saugventil an und presst es durch das Druckventil
wieder in das Druckrohr zurück; hierbei findet wohl kein erheblicher Arbeitsverlust
statt, allein es besteht der Uebelstand, dass die beiden Ventile beständig
fortklappern. Besser ist es daher, das Druckrohr mit dem Pumpenstiefel in Verbindung
zu setzen, wodurch man das erwünschte Resultat erzielt, ohne dass die beiden Ventile
zur Hebung gelangen; es verbleibt aber noch der Nachtheil, dass die Druckwassersäule in
beständige, periodische Bewegung versetzt wird. – Wenn das untere Saugventil nicht
angebracht ist, so kann man auch das Saugrohr mit dem Pumpenstiefel in Verbindung
bringen, wobei sowohl die beiden Ventile, als auch die Druckwassersäule in Ruhe
verbleiben. Ist das untere Saugventil vorhanden, so wird diese Verbindung
unbrauchbar, da dann die Pumpe fortwirkt, nur mit dem Unterschiede, dass statt des
obern Saugventiles das untere in Thätigkeit tritt.
2) Wohl am häufigsten wird das Abstellen der Pumpen dadurch bewerkstelligt, dass man
den Lufthahn g (Fig. 3) öffnet; dies ist
aber die am wenigsten empfehlenswerthe Methode. Erstlich fällt hierbei die
Saugwassersäule jedesmal herab, wenn das untere Saugventil f, wie gewöhnlich, nicht vorhanden ist; in Folge dessen versagt dann die
Pumpe leicht beim Anlassen. Ferner wirkt die Pumpe auf diese Art als Luftpumpe mit
beständigem Spiele der Ventile fort, saugt nämlich Luft durch den Hahn g an und presst diese in die Druckleitung. Daher ist
zum Leergange der Pumpe eine gewisse Arbeit E0 erforderlich, welche sich zu der beim Vollgange
nöthigen Arbeit E, wie leicht nachweisbar, in folgendes
Verhältniss stellt:
\frac{E_0}{E}=\frac{x}{x-1}\,\frac{\left(\frac{p}{\frakfamily{H}}\right)^{\frac{x-1}x}-1}{\frac{p}{\frakfamily{H}}-1},
wobei x=1,41 das bekannte Verhältniss der
beiden Wärmecapacitäten der Luft bedeutet. Setzen wir z.B. für eine
Kesselspeisepumpe p=6^{at} und
\frakfamily{H}=1^{at}, so findet sich nach der obigen Formel
E_0=0,47\;E. Die Arbeit zum Leergange der Pumpe beträgt also
hier ungefähr die Hälfte von jener, welche zum Vollgange erforderlich ist.
3) Das beste Mittel zum Abstellen der Pumpe besteht in der Oeffnung des Hahnes a (Fig. 3) oder des
Lufthahnes b, wenn dieser gross genug ist. Die Pumpe
saugt dann durch den geöffneten Hahn Luft an und treibt diese beim Rücklauf des
Plungers auf demselben Wege wieder hinaus; hierzu ist weder ein Arbeitsaufwand
erforderlich, noch treten die beiden Ventile in Thätigkeit; auch bleibt der
schädliche Raum mit Wasser gefüllt und somit kann die Pumpe meistens ohne Anstand in
vollen Betrieb gesetzt werden. Statt eines Absperrhahnes kann man für diesen Zweck
mit Vortheil ein stellbares Ventil verwenden, wie solches in Fig. 6 Taf. 14 dargestellt
ist; dasselbe öffnet sich nach innen, damit der Luftabschluss beim Gange der Pumpe
vollkommen erfolge.
Wir gelangen nun zur zweiten Gruppe der Pumpen, nämlich:
b) Solche, welche selbstthätig, ohne vorherige Füllung mit Wasser, zur Wirksamkeit gelangen können.
Diese Pumpen bestimmen sich nach Gleichung (15) durch die Relation
(k+1)\,H<\frakfamily{H}, welcher Bedingung z.B. eine
Pumpe mit der Saughöhe H=5^m und dem schädlichen Raume
k=0,1 (10 Proc.) genügt. Diese Pumpen, die mit Luft in allen
Räumen durch das Kolbenspiel allein zum Wasserschöpfen gebracht werden können,
bedürfen folgender Armirung:
1) Das zweite Saugventil f (Fig. 3) kann
entfallen.
2) Hingegen muss, mit dem Innern des Pumpenstiefels an der höchsten Stelle verbunden,
ein Hilfsdruckventil, etwa wie Fig. 7 Taf. 14 näher
zeigt, angebracht werden, welches mit der äussern Atmosphäre in Verbindung steht.
Auf diese Weise wird nämlich die Compression der aus dem Stiefel auszutreibenden
Luft auf die Spannung, welche der Druckhöhe entspricht, vermieden; die Luft wird
also nicht mehr durch das Druckventil in die Druckleitung gepresst, sondern gelangt
ohne Verdichtung in die äussere Atmosphäre, womit ein Uebelstand beseitigt wird,
welchem in den meisten Fällen das Versagen der Pumpen beizumessen ist. Dem
angeführten Zwecke entsprechend, lässt man das obige Hilfsdruckventil so lange
thätig, bis der Stiefel vollständig mit Wasser gefüllt ist und durch das Ventil
Wasser ausspritzt; hierauf wird das Ventil, durch eine Stellschraube auf seinen Sitz
niedergedrückt, bezieh. geschlossen. Während dieser Zeit kann man die Pumpe ohne
Anstand schnell laufen lassen, wenn sich in der Druckrohrleitung blos Luft befindet.
Ist hingegen, wie gewöhnlich, die Druckrohrleitung mit Wasser gefüllt, so wird man
gut daran thun, die Pumpe langsam angehen zu lassen, besonders in jenem Augenblick,
wo das Hilfsdruckventil geschlossen und darauf unmittelbar die ganze
Druckwassersäule in Bewegung gesetzt wird, um einen gefährlichen Stoss zu vermeiden;
diese Vorsicht wird um so nöthiger, wenn kein Druckwindkessel vorhanden ist.
3) Für das Abstellen dieser Art Pumpen gelten dieselben Grundsätze und sind die
gleichen Vorkehrungen anwendbar, welche bei den Pumpen der ersten Gruppe namhaft
gemacht wurden.
Verschiedene andere Erfordernisse der Pumpen. Zu diesen
gehören vor Allem der Druck- und Saugwindkessel, deren Zweck hier keiner Erörterung
bedarf; es wird blos einiges über die Speisung der Druckwindkessel mit Luft zu
bemerken sein. Die Windkessel sind nämlich niemals vollkommen luftdicht; bei solchen
aus Schmiedeisen entweicht die Luft durch die Nieten und Ueberlappungen der Bleche,
bei den gusseisernen Windkesseln aber durch die Poren des Metalles. Der hierdurch
bedingte Luftabgang wird zwar zum Theil durch den Luftgehalt des Wassers ersetzt,
der beim Ansaugen frei und in der Folge an den Windkessel abgegeben wird; trotzdem
zeigt es sich, dass der Luftgehalt im Windkessel nach und nach abnimmt weshalb es
nöthig wird, demselben
entweder ununterbrochen oder zeitweilig Ersatzluft zuzuführen. Diesen Zweck erreicht
man am einfachsten durch ein kleines, freifallendes Ventil, welches sich, wie Fig. 8 Taf. 14
zeigt, gegen das Innere des Pumpenstiefels öffnet; durch dieses Hilfsventil wird nun
bei jedem Hub eine kleine Menge Luft angesaugt und bei dem nächstfolgenden Hube in
die Druckrohrleitung gepresst, von wo sie in den Windkessel gelangt. Zur Regulirung
des Luftzuflusses kann entweder der Hub des Ventiles entsprechend verstellt werden,
oder es wird hierzu ein Absperrhahn benutzt.
Nach längerem Stillstande der Pumpe wird es nöthig sein, bei der Wiederingangsetzung
derselben dem Windkessel auch eine grössere Menge Luft zuzuführen; hierzu kann
dieselbe Vorrichtung, die in Fig. 8 dargestellt ist,
verwendet werden; nur muss der Hahn vollständig geöffnet werden, um den Luftzutritt
zu erleichtern. Man hat aber hierbei zwei Fälle zu unterscheiden.
Wenn für die Pumpe nach Gleichung (1) die Relation
\frac{1+k}{k}\,\frakfamily{H}>p zutrifft, so kann die Füllung
des Windkessels mit Luft ohne weiteres durch den genannten Apparat bewirkt werden,
weil unter dieser Bedingung die comprimirte Luft das Druckventil zu heben
vermag.
Ist hingegen \frac{1+k}{k}\,\frakfamily{H}\leqq p, so muss vorerst
das Hilfsdruckventil (Fig. 7) in Thätigkeit
gesetzt und der Pumpenstiefel theilweise mit Wasser gefüllt werden. Sobald dies
geschehen ist, wird das Hilfsdruckventil abgestellt und statt dessen das
Hilfssaugventil (Fig. 8) in Thätigkeit versetzt. Die theilweise Füllung des Pumpenstiefels
mit Wasser ermöglicht nun, die angesaugte Luft so weit zu verdichten, dass sie ihren
Weg wieder durch das Druckventil nehmen kann, was sonst nicht möglich gewesen
wäre.
Man muss jedoch Sorge tragen, das Hilfssaugventil (Fig. 8) jederzeit so
anzubringen, dass sich die angesaugte Luft direct unter dem Druckventil ansammeln
kann; denn nur in diesem Falle wird sie während der Compression durch das sich
hebende Druckventil entweichen; andernfalls würde sich die Luft an der höchst
gelegenen Stelle des Pumpenstiefels ansammeln und dort verbleiben. Dieser Fall ist
besonders bei den vertical stehenden Plungerpumpen zu beachten. So z.B. dürfte in
Fig. 5 das
Hilfssaugventil nicht unmittelbar am Plungercylinder angebracht sein, weil sich die
angesaugte Luft oben bei der Plungerstopfbüchse ansammeln würde, in welchem Raume
sie auch während des Niederganges verbleibt. Der Platz des Hilfssaugventiles ist
dann bei k, unmittelbar unter dem Druckventil, für
welchen Fall demselben eine ähnliche Form, wie in Fig. 9 Taf. 14
dargestellt, zu geben ist. Mit der Zeit wird sich aber doch bei der Stopfbüchse oben
die aus dem Wasser frei werdende Luft anhäufen; um diese selbstthätig zu entfernen, hat man bei l (Fig. 5) ein
Hilfsdruckventil nach Fig. 9 anzubringen, durch
welches die Luft in die Druckrohrleitung gelangt; sonst wirkt dieses Ventil, wenn
grade keine Luft vorhanden ist, in gleicher Weise, wie das eigentliche
Druckventil.
Derselbe Zweck, nämlich die Luftentfernung, lässt sich, minder bequem, auch dadurch
erreichen, dass man beim Niedergang den Hahn b (Fig. 5) öffnet,
was bei langsamem Gange keinem Anstände unterliegt. Der Hahn b kann auch benutzt werden, wenn die Pumpe mit Wasser gefüllt wird, um die
Luft aus dem obersten Raume zu entfernen; denselben Dienst leistet übrigens auch das
Hilfsdruckventil l (Fig. 5) selbstthätig.
Zur Füllung des Windkessels mit Luft lässt sich auch ein Apparat, der auf dem
Pumpenstiefel aufgesetzt wird, verwenden, in welchem ein Saugventil und ein
Druckventil vereint wirken; die comprimirte Luft streicht dann nicht mehr durch das
Druckventil der Pumpe, sondern wird dem Windkessel direct durch ein besonderes Rohr
zugeführt. Ein solcher Apparat, von Riehn construirt,
ist in D. p. J. *1877 226
132 beschrieben. (Vgl. auch Wippermann und Lewis, S. 231 dieses Bandes.)
Pumpen, deren Druckrohrleitung eine ansehnliche Höhe oder Länge besitzt, müssen über
dem eigentlichen Druckventil, wie in Fig. 5, noch ein zweites
Druckventil m erhalten: dasselbe ist nicht freifallend,
sondern meistens zum Stellen eingerichtet; beim Gange der Pumpe ist es gänzlich
aufgezogen; hingegen wird es geschlossen, wenn die Liderung des untern Druckventiles
auszuwechseln oder sonst etwas an diesem nachzusehen oder auszubessern ist. Hierbei
würde es sehr stören, wenn man, um dies zu ermöglichen, das Wasser in der
Druckrohrleitung jedesmal ablassen müsste, welcher Unbequemlichkeit durch die
Anwendung eines derartigen Ventiles auf einfache Weise abgeholfen wird.
Regulirung der geförderten Wassermenge. In den
Tiefbauschachten stehen gewöhnlich mehrere Saug- und Druckpumpen über einander, so
dass das von der untersten Pumpe gehobene Wasser der nächst höhern u.s.f. geliefert
wird. Wenn diese Pumpen auch gleiche Abmessungen und eine gemeinschaftliche Hubhöhe
besitzen, so kann doch nicht angenommen werden, dass sie, eine wie die andere,
gleiche Wassermengen fördern, schon darum nicht, weil sie sich voraussichtlich nicht
sämmtlich in gleich gutem Zustande befinden. Hebt nun eine Pumpe mehr Wasser als die
nächst höhere, so wird sich das Wasser im Steigrohr der erstem allmälig höher
stellen und schliesslich überlaufen; damit ist wohl ein Effectverlust verbunden, den
man sich aber gefallen lassen kann, wenn die überlaufende Wassermenge nicht
unverhältnissmässig gross ist. Zuweilen sucht man diesen Fall sogar absichtlich
dadurch herbeizuführen, dass man die Plungerdurchmesser der auf einander folgenden Drucksätze in
der Richtung von oben nach unten um eine Kleinigkeit zunehmen lässt. Hebt jedoch
eine Pumpe mehr Wasser als die zunächst unten befindliche, so wird der Wasserspiegel
im Steigrohr der letztem nach und nach fallen und die obere Pumpe schliesslich Luft
ziehen – ein Uebelstand, der ungleich nachtheiliger ist als das Ueberlaufen des
Wassers im Steigrohr.
Um einer solchen Störung vorzubeugen, hat man in Fig. 5 bei l ein Hilfsdruckventil (Fig. 9) anzubringen, lässt
aber jetzt das Wasser nicht in die Druckrohrleitung, sondern in das Steigrohr S des untern Drucksatzes gelangen. Auf diese Weise wird
das von dem obern Drucksatz zu viel angesaugte und geförderte Wasser wieder
zweckentsprechend und ohne bemerkenswerthen Effectverlust zurückgeleitet. Rinder
bequem ist es, zum gleichen Zwecke, das Wasser aus dem obern Steigrohr in das untere
einfach abzulassen.
Prüfung der Pumpen. Wenn eine Pumpe beim Anlassen
versagt, so kann der Grund zunächst in der Undichtheit der Plungerstopfbüchse
bezieh. des Pumpenkolbens oder an sonstigen undichten Stellen gröberer Art im
Pumpenstiefel liegen. Um sich hiervon zu überzeugen, öffne man das Abstellventil
Fig. 6
oder den Lufthahn b bezieh. c in Fig.
3; findet man, dass die Luft daselbst angesaugt und ruckweise ausgestossen
wird, so sind keine Undichtigkeiten an den oben angeführten Bestandtheilen
vorhanden. Findet hingegen kein genügend deutlich begrenztes Ausstossen der Luft bei
den genannten Oeffnungen statt, so ist es auch möglich, dass die Ventile nicht
gehörig wirken. Angesaugte, grössere Holzstücke oder sonstige Körper können
verhindern, dass sich die Ventile schliessen; bei Teller- und Glockenventilen
zwängen sich häufig kleine Splitter in die Führungen und das Ventil bleibt offen
stecken; bei kleinen Pumpen versagen die Ventile schon dann ihren Dienst, wenn auf
dem Sitze grobe Sandkörner haften, Oftmals genügt es hierbei, wenn man den Deckel
des Ventilgehäuses über dem Druckventil öffnet und Wasser durchgiesst.
Zeigt sich jedoch in Hinsicht der Dichtigkeit Alles in Ordnung, so hat man zu
unterscheiden, ob die Pumpe zur oben angeführten Gruppe a oder b gehört. Im erstem
Falle kann die Saugwassersäule abgelaufen sein, wenn das untere Saugventil f (Fig. 3) undicht oder
geklemmt ist; oder die Saugwassersäule ist abgerissen, wenn das untere Saugventil
f fehlt; oder endlich hat sich im Pumpenstiefel
eine grössere Menge Luft angehäuft. Es bleibt dann nichts übrig, als die Saugleitung
und den Pumpenstiefel frisch mit Wasser zu füllen.
Gehört die Pumpe zur Gruppe b, so wird man das Hilfsdruckventil Fig. 7 spielen lassen, um
die Luft aus allen Räumen zu entfernen. Ist ein solches Ventil nicht vorhanden, so
muss man sich auf andere Weise behelfen. Steht z.B. der Lufthahn b oder c (Fig. 3) zur Verfügung, so wird man denselben,
während der Plunger drückt, offen halten, hingegen beim Ansaugen schliessen.
Bei den Kesselspeisepumpen, bei welchen die Höhe der Druckrohrleitung zumeist
unerheblich und der Speisekopf mit freifallendem Ventil versehen ist, schalte man
einen Ablasshahn in die Druckleitung ein; dieser wird beim Ansetzen der Pumpe so
lange offen gehalten, bis dieselbe Wasser fasst und letzteres durch den Hahn
ausgespritzt wird. Während dieser Zeit wird nämlich auch auf solche Art das
Druckventil entlastet, und hieraus erklärt sich die Wirksamkeit des obigen Hahnes;
ist letzterer selbst nicht vorhanden, so hilft sich der Wärter wohl auch damit, dass
er den Deckel des Ventilgehäuses, welcher sich über dem Druckventil befindet, etwas
lüftet, bis durch die gebildete Oeffnung Wasser ausspritzt, wodurch der gleiche
Zweck, nämlich die Entlastung des Druckventiles, auf minder bequeme Weise erzielt
wird. Nach längerer Unterbrechung der Speisung des Dampfkessels wird das im
Speiserohr zurückgebliebene Wasser zuweilen sehr heiss, besonders wenn die
Speiseleitung kurz und das Rückfallventil im Speisekopf oder dessen Sitz undicht
ist. In diesem Falle entwickelt sich im Speiserohr Dampf, der auf das Druckventil
presst und so beim Anlassen der Pumpe hinderlich einwirkt. Auch für diesen Fall
leistet ein Ablasshahn in der Speiseleitung, bezieh. das Lüften des Ventildeckels
entsprechende Dienste. Die Entlastung des Druckventiles kann übrigens hier auch
durch Abkühlung des Speiserohres mit kaltem Wasser bewirkt werden, wobei sich der
Dampf condensirt und ein Vacuum im Speiserohr entsteht, worauf die Pumpe unmittelbar
zu wirken beginnt.
Tafeln