| Titel: | Ueber Constructionsverhältnisse von Fallblöcken der Dampfhämmer. |
| Fundstelle: | Band 227, Jahrgang 1878, S. 340 |
| Download: | XML |
Ueber Constructionsverhältnisse von Fallblöcken
der Dampfhämmer.
Mit Abbildungen auf Tafel
21.
Ruchholz, über Fallblöcke der Dampfhämmer.
Emil
Ruchholz veröffentlicht in der Zeitschrift des
Vereines deutscher Ingenieure, 1877 S. 169 die
Resultate angestellter Vergleiche von Fallblöcken einer grössern Anzahl ausgeführter
Dampfhämmer mit dünner Kolbenstange, wovon wir hier das Wesentlichste mittheilen.
Die Betrachtungen gelten fast ausschliesslich nur für solche Hämmer, welche durch
Schmieden von Stahl stark beansprucht werden, wie dies bei dem Verarbeiten der
Bessemerstahlblöcke der Fall ist.
Die Bedingungen, welche ein Hammerbär zu erfüllen hat, sind der Hauptsache nach
folgende: 1) muss derselbe das nöthige Fallgewicht herstellen, 2) das Werkzeug oder
den Kern fassen, 3) das Werkzeug in einer bestimmten Bahn, d.h. lothrecht führen, 4) den
Angriffspunkt der Kraft (die Kolbenstange) fassen.
Nimmt man das Gewicht von Hammerkern und Kolbenstange sammt Kolben im Mittel mit ¼
des Fallgewichtes an, und bezeichnet Gk das gesammte Fallgewicht, Pk das Bärgewicht, so
ist P = 0,75 G.
Bei der Befestigung des Hammerkernes am Bär sind Einfachheit und leichte Lösbarkeit
Hauptbedingungen. Die Construction mit schwalbenschwanzförmigen Zapfen ist häufiger
in der Praxis zu finden als jene mit rundem Stiel, obwohl letztere die
vortheilhaftere zu sein scheint, da die Bearbeitung des Schwalbenschwanzes nicht so
einfach und leicht, als dies beim Stiel der Fall ist. Der schwalbenschwanzförmige
Zapfen ist wohl weniger dem Brechen ausgesetzt, weil der Bruchquerschnitt grösser
als beim runden Stiel ausfällt. Dagegen werden die Nasen am Bär stark beansprucht
einestheils durch den Keil, anderntheils aber können bedeutende Inanspruchnahmen
stattfinden, wenn die Fläche des Kernes einseitig oder nur in der Mitte aufliegt.
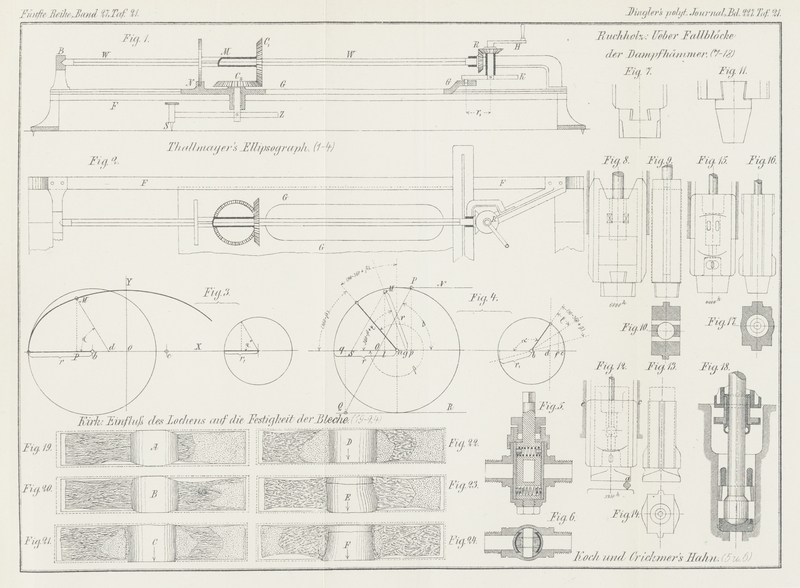
Fig. 7
Taf. 21 zeigt eine Construction, welche dies zu vermeiden sucht. Es sind hier die
Nasen am Stöckel, so dass beim Festkeilen desselben nur dieser stark beansprucht
wird. Fig. 8
bis 10 Taf.
21 zeigen die gewöhnliche Befestigungsart mit einem Keil, während bei Fig. 11 zwei
Keile angewendet sind. Einen dieser Keile gestaltet man gewöhnlich als Beilage mit
Nasen an den Enden, um eine Verschiebung des Kernes nach vor- und rückwärts
aufzuheben. Zweck dieser Anordnung ist, eine seitliche Verschiebung des Stöckels zu
ermöglichen für den Fall, in welchen die Schabotte sich seitlich verschoben hat. Die
Fig. 12
bis 17 Taf.
21 zeigen die Anordnung mit einem Stiel, wobei die Befestigung durch einen Keil
erfolgt. Der Bär wird hier insofern günstiger beansprucht, als man ein Ausreissen
des Keilloches nicht zu fürchten hat; dagegen wird der Kern stark in Anspruch
genommen, namentlich wenn der Keil nicht gleichmässig aufliegt.
Die Führung des Bars zwischen den Ständern bildet einen der wesentlichsten Punkte der
ganzen Hammerconstruction. Vor allen Dingen ist hier erforderlich, dass der
Hammerbär ein genügendes Stück in den Führungen bleibt, wenn er seine tiefste
Stellung einnimmt. Bei seitlichem Aufschlagen (Fig. 7) entsteht ein
Moment, welches den Hammerbär um a zu drehen sucht;
dieses Bestreben wird durch den Widerstand bei e
aufgehoben. Letzterer aber wird um so kleiner, je grösser die Entfernung ac ist. Es werden daher die Führungen um so weniger
leiden, je länger der Bär ist.
Die Mehrzahl der in den Vergleich gezogenen Beispiele lässt den Hammerbär in der
tiefsten Stellung so weit aus den Führungen treten, dass die Unterkante derselben
die Länge von Bär und Stöckel nahezu halbirt. Skizzen von grossen englischen Hämmern
zeigen die Unterkante der Führungen noch tiefer gelegt. Als bewährtes Verhältniss
kann man wohl
setzen, dass die Führungsunterkante die Länge von Bär und Stöckel halbiren soll.
Als mittlere Verhältnisse ergeben sich für die Dimensionen des Bärs:
L\ddot{a}nge\ L:Breite\ B:Dicke\ D=9:4:3, womit sich für
P=0,75\,G, wenn L, B und D in Millimeter ausgedrückt sind, ergibt:
L=90\sqrt[3]G, B=40\sqrt[3]G,
D=30\sqrt[3]G, welche Verhältnisse für Hämmer über 5t gut passen, für kleinere Hämmer aber einer
Berichtigung bedürfen, wenn nicht schon Höhlungen und sonstige constructive Formen
ein leichteres Gewicht ergeben. Dieselben stimmen mit Fig. 15 und 16 ziemlich
überein, und haben sich Hämmer nach dieser Construction bei bedeutender
Inanspruchnahme gut bewährt. In Fig. 8, 9, 12 und 13 sind diese
Verhältnisse punktirt angedeutet. Bei dem Hammerbär Fig. 12 und 13 hatte das
Hammergerüst bedeutend zu leiden; bei jenem Fig. 8 und 9 überschreiten die
Längendimensionen und suchen die Führung noch dadurch zu verlängern, dass die
Stopfbüchse zwischen zwei den Bär verlängernde Lappen tritt. Schöner und
constructiver ist derselbe Zweck in Fig. 12 bis 17 erreicht,
indem hier für die Stopfbüchse eine cylindrische Aussparung angebracht ist.
Die Führungen an den Ständern findet man meist unnützer Weise nach oben zu lang. Für
diese genügt als Länge vollständig der grösste Hub. Es tritt dann der Bär nach unten
⅖ aus den Führungen und bleibt in der höchsten Stellung noch mit ⅖ zwischen
denselben, wenn die Höhe des Hammerkernes mit ⅕ der ganzen Bärlänge angenommen
wird.
Es erübrigt noch die Befestigung der Kolbenstange am Bär. Beim Niedergang des Hammers
entsteht hier ein Stoss zwischen Kolbenstange und Bär, bei welchem die lebendige
Kraft der Stange sammt Kolben vernichtet wird. Dieser Stoss wirkt auf Zerstörung der
untern Fläche der Kolbenstange und der zugehörigen Fläche des Bars. Um die
Zerstörung dieser Flächen möglichst lange zu verhüten, wird man daher gezwungen
sein, den Stoss hier elastisch zu machen, oder die Rächen derart zu vergrössern,
dass eine statthafte Abnutzung eintritt. Um diese Verbindung elastisch zu machen,
ist viel versucht worden, doch alles ohne Erfolg.
Eine der einfachsten Befestigungen gibt die nach unten schwach verjüngte, durch einen
durchgehenden Keil mit dem Bär verbundene Kolbenstange. Hier wird bei jedem Schlage
die Kolbenstange bei dem Querschnitte durch das Keilloch gestaucht, bis der Bruch
eintritt. Eine Verstärkung der ganzen Stange, um diesen Querschnitt gross genug zu
erhalten, ist zwecklos, weil mit der Verstärkung auch das zerstörende Moment grösser
wird. Entschieden fehlerhaft ist es, die Stange hier abzusetzen; richtiger ist es,
sie unten zu verstärken, so lass durch das Keilloch keine Schwächung eintritt. Doch
wird man bei Hämmern mit
Oberdampf auch hiermit noch schlecht auskommen, besonders wenn der Bär eine
durchgehende Oeffnung für die Bohrstange hat, wie bei den mit runden Stielen
eingesetzten Kernen Fig. 12 und 15. In anderer Weise ist
die Aufgabe in Fig.
8 gelöst; hier ist die Kolbenstange in rationeller Weise unten verstärkt
und durch zwei Streifkeile gehalten. Man hat hierbei nur darauf zu sehen, dass die
Belastung der Keile 10k auf 1qmm nicht übersteigt. In Fig. 12 und 15 ist die
Stange unten gleichfalls verstäkt, aber am untern Ende kugelförmig abgedreht. Mit
dieser Kugelfläche stützt sich die Stange auf ein Stahlstück, oberhalb der
Verstärkung liegt sie passend an zwei durch einen Ring zusammen gehaltene Backen.
Fig. 18
Taf. 21 zeigt die Ausführung dieser Verbindung für den in Fig. 15 gezeichneten
Fallblock in 1/20
u. G. Trotz der vielen Theile, welche diese Anordnung bedingt, hat dieselbe doch
eine grosse Haltbarkeit gezeigt und ist ganz besonders günstig für die
Inanspruchnahme der Kolbenstange, indem sich unten die Kugel der Stangenrichtung
gemäss verdreht, wenn sich die Kolbenstange oben biegt.
Kolbenstangenbrüche sind häufig, wenn der Bär kurz, also schlecht geführt, und wenn
die Stange fest eingekeilt ist. Bezüglich der Beanspruchung der Kolbenstange ergibt
sich angenähert, wenn G' das Kolbenstangengewicht sammt
dem des Kolbens, V die Geschwindigkeit von G' beim Aufschlagen, s die
Zusammendrückung der Kolbenstange, P' den grössten
stattfindenden Druck zwischen Stange und Unterlage bezeichnen und absolut feste
Unterstützung vorausgesetzt wird, da P' von O bis P wächst:
1/2\,P's=1/2\,MV^2,\;M=\frac{G'}{g},\;\frac{V^2}{2}=gh,\;1/2\,P's=G'h.
Ist E der Elasticitätsmodul der
Stange, l deren Länge, f
deren Querschnitt, so ist
s:l=\frac{P'}{f}:E oder s=\frac{P'l}{fE},
daher
1/2\,P'^2\,\frac{l}{fE}=G'h oder
P'=\sqrt{\frac{2\,G'hfE}{l}}.
Für die Stange Fig. 18 ist
h=1700, wozu die Wirkung des Oberdampfes noch mit 1m kommt, f=10387^qmm,
G'=350^k, E=20000,
l=2700. Es wird P=381500^k und ergibt sich
ein Flächendruck von 9k auf 1qmm, welche Beanspruchung ziemlich der
Wirklichkeit entsprechen dürfte. Durch das Antreiben der Keile werden nämlich schon
ziemlich bedeutende Spannungen hervorgerufen, daher die Nachgiebigkeit der Schabotte
wohl ausser Betracht bleiben kann.
Tafeln