| Titel: | Apparate zum Verzeichnen von Parabeln; von Prof. V. Thallmayer in Ungarisch-Altenburg. |
| Autor: | V. Thallmayer |
| Fundstelle: | Band 227, Jahrgang 1878, S. 430 |
| Download: | XML |
Apparate zum Verzeichnen von Parabeln; von Prof.
V. Thallmayer in
Ungarisch-Altenburg.
Mit Abbildungen auf Tafel
28.
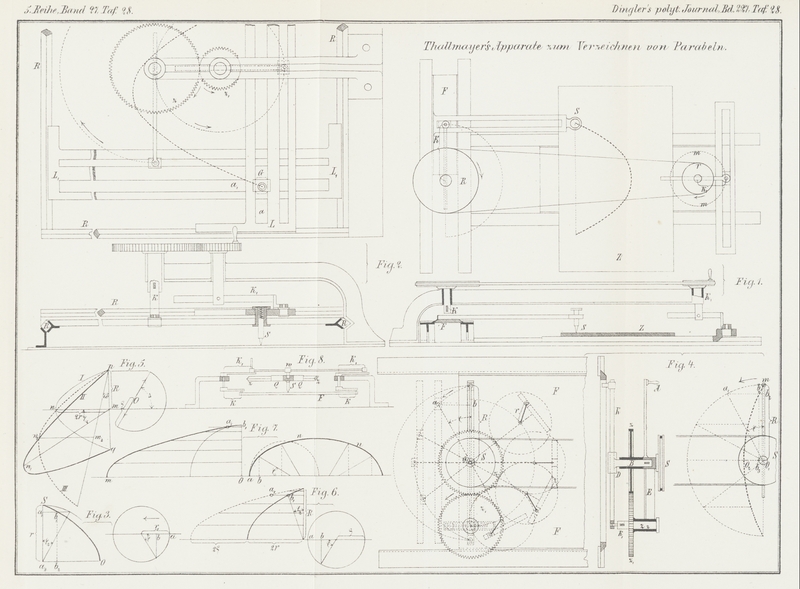
Thallmayer's Apparate zum Verzeichnen von Parabeln.
Im Anhange an meine Ellipsographen (S. 337 d. Bd.) seien nachstehend einige auf Tafel 28 dargestellte Apparate angeführt, welche zur
Verzeichnung von Parabeln verwendet werden können. Der in Fig. 1 veranschaulichte
Apparat zeichnet Parabeln auf einer in geradlinig schwingender Bewegung befindlichen
Unterlage; der Apparat Fig. 2 hingegen ist zum
Verzeichnen von Parabeln auf in Ruhe befindlichen Unterlagsflächen geeignet.
In dem ersten Apparate, dessen Anordnung aus der Abbildung klar genug zu ersehen ist,
sind R und r Scheiben mit
dem Uebersetzungsverhältnisse ½. Demgemäss entfällt auf ein einmaliges Hin- und
Herschwingen oder auf eine volle Schwingung des Zeichenbretes Z nur eine halbe Schwingung des Stiftes S, der unter diesen Umständen, wie sich leicht nachweisen lässt,
eine Parabel beschreibt. Haben die Kurbelschienen K und
K' eine andere Anfangsstellung, als die in Fig. 1
angenommene, d.h. sind sie unter beliebigem Winkel zu einander gekehrt, so
beschreibt der Stift S keine Parabel sondern Curven,
deren Gleichung vom vierten Grade ist.
Dass der Stift S unter den oben
erwähnten Verhältnissen eine Parabel beschreibt, lässt sich mit Hilfe der Fig. 3
nachweisen. Bezeichnet nämlich r die zur Wirkung
kommende Länge der Kurbelschiene K und r1 jene der
Kurbelschiene K1, so
ist nach einer Drehung der letzteren um den Winkel φ
aus der Anfangslage der Stift S um das Stück
r\left(1-cos\,\frac\varphi 2\right) nach abwärts gerückt und
gleichzeitig die Zeichenbretfläche um das Stück
ab=r_1(1-cos\,\varphi) in der Richtung des Pfeiles verschoben
worden. Es kommt daher nicht der Punkt a1 unter den Stift zu stehen, sondern ein Punkt,
welcher um die Strecke a_1b_1=ab vor der Linie Sa2 liegt. Nimmt man
nun den Punkt O, der von der Linie Sa2 in der Entfernung 2r1 liegt und über welchem sich der Stift
S befindet, wenn die Kurbelschiene K1 eine halbe Umdrehung
vollführt hat, als Ursprung eines rechtwinkligen Coordinatensystemes an, so ist mit
Berücksichtigung dessen, dass dann der Stift S sich
auch um das Stück Sa_2=r herabbewegt hat, b1b2 die Ordinate y und
Ob2 die Abscisse
x des Punktes b1. Nun ist b_1\,b_2=y=r\,cos\,\frac\varphi
2 und Ob_2=x=r_1(1+cos\,\varphi) und hieraus ergibt
sich durch Elimination von φ die Gleichung einer
Parabel nämlich: y^2=\frac{r^2}{2\,r_1}x.
Der in Fig. 2
abgebrochen gezeichnete Apparat, welcher, wie schon bemerkt, auf in Ruhe
befindlicher Unterlagsfläche Parabeln verzeichnet, besteht der Hauptsache nach aus
einem viereckigen Rahmen, dessen Seitentheile R
gleichzeitig Führungsschienen für die Lineale L und L1
bilden, von denen sich L über L1 befindet. Beide
Lineale werden durch Kurbelschienen in schwingende Bewegung versetzt, und zwar
entfällt auf eine vollständige Schwingung des Lineales L nur eine halbe Schwingung des Lineales L1, was durch die Zahnradübersetzung z1 : z = 1 : 2 erreicht wird. Der Stift eines an der
Kreuzungsstelle der zwei Ausschnitte a und a1 eingesetzten
Gleitstückes G wird dann bei eintretender Bewegung in
einer Parabel geführt, was nach Obigem besonders zu beweisen nicht nöthig ist.
Ist bei beiden besprochenen Apparaten die Uebersetzung von Kurbelschiene auf
Kurbelschiene gleich 1, so beschreiben die Stifte Ellipsen. Apparat Fig. 2 ist demnach, wenn
man ein Zahnräderpaar mit dem Uebersetzungsverhältnisse 1 zum Auswechseln hat, auch zur Verzeichnung von Ellipsen auf dem Zeichenbrete
zu gebrauchen; denn es lässt sich hierfür leicht die Anordnung treffen, dass die
zwei Kurbelschienen sich nicht im Wege stehen. Zieht man die Kurbelschienen aus den
Zapfen der Räder heraus, so kann der Apparat auch zum Ziehen
von parallelen und senkrechten Linien verwendet werden.
Wenn in Fig. 1
die Warze der Kurbelschiene bei ihrer Drehung statt eines Kreises mm eine Ellipse nn, wie in
Fig. 7,
beschreibt, so verzeichnet der Stift S auf dem nunmehr
durch elliptische Bewegung der Kurbelwarze zur Schwingung veranlassten Zeichenbrete
ebenfalls eine Parabel, was sich leicht nachweisen lässt. Die Kurbelwarze könnte
entsprechend der bei dem Ellipsographen (S. 337 d. Bd.) getroffenen Anordnung leicht
in einer Ellipse geführt werden.
Lässt man unter dem Apparate Fig. 2 die
Unterlagsfläche, während das Gleitstück G in einer
Parabel sich bewegt, unter einem beliebigen Winkel A
zur Richtung des Lineales L1 entweder eine volle oder eine halbe Schwingung vollführen (durch eine in
einen Schlitz der Unterlagsfläche einspielende Kurbelschiene), so verzeichnet der
Stift des Gleitstückes G auf ihr ebenfalls
Parabeln.
In Fig. 5 ist mit Δ der Winkel, unter welchem
die Schwingung vor sich geht und mit I die Parabel
bezeichnet, die der Stift bei in Ruhe befindlicher Unterlagsfläche auf ihr
beschreiben würde. Bei den in Fig. 5 angenommenen
Kurbelschienenlängen würde der Stift bei einer vollen Schwingung der Unterlagsfläche
die Parabel II und bei einer halben die Parabel III verzeichnen.
Ist R die Länge der in das Lineal L1 eingreifenden, r die Lange der in das Lineal L eingreifenden Kurbelschiene und g die Länge
jener Kurbelschiene, welche die unter dem Winkel Δ vor
sich gehende schwingende Bewegung der Unterlagsfläche veranlasst, so findet man als
Gleichung der Parabel II, bezogen auf ein
schiefwinkliges Coordinatensystem mit dem Ursprung in
n_1,\;y^2=\frac{R^2}{2\sqrt{\varrho^2+r^2+2\,r\varrho\,cos\,\Delta}}\,x,
wobei n_1\,m=2\sqrt{\varrho^2+r^2+r\varrho\,cos\,\Delta} die
Abscissenachse ist, die von der Richtung des Lineales L1 um den Winkel ψ absteht, dessen Tangente sich durch die Formel
tg\,\psi=\frac{\varrho\,sin\,\Delta}{r+\varrho\,cos\,\Delta}
ergibt. Die Ordinatenachse pq ist parallel zum Lineale
L.
Ebenso findet sich als Gleichung der Parabel III, bezogen auf ein schiefwinkliges Coordinatensystem
mit n2 als Ursprung,
y^2=\frac{\varrho^2+R^2+2\,R\varrho\,sin\,\Delta}{2\,r}\,x.
Hierbei liegt die Abscissenachse m2n2 parallel zur Richtung des Lineales L1 und um das Stück ρ sin Δ senkrecht von der Linie mn entfernt. Die Ordinatenachse schliesst mit der Richtung des Lineales
L den Winkel ω, für
welchen
tg\,\omega=\frac{\varrho\,cos\,\Delta}{R+\varrho\,sin\,\Delta}.
Fig. 6
entspricht der Annahme, dass die Schwingung der Unterlagsfläche des Apparates Fig. 2 parallel
zu dem Lineale L1 vor
sich geht. Hierbei bewegt sich das Gleitstück G in der
voll ausgezogenen Parabel und der darin befindliche Stift beschreibt auf der in
Bewegung befindlichen Unterlagsfläche die punktirt gezeichnete Parabel. Würde die
Unterlagsfläche des Apparates Fig. 2 durch die
elliptische Bewegung einer Kurbelwarze in Schwingung versetzt werden, so würden
analog dem Falle in Fig. 5 vom Stifte des Gleitstückes auf ihr ebenfalls Parabeln verzeichnet
werden.
Wollte man ähnlich wie bei dem älteren Ellipsographen (*1877 226 237) auf einer in schwingende Bewegung versetzten Unterlagsfläche von
einer einen Kreis beschreibenden Zirkelschiene Parabeln verzeichnen lassen, so
könnte man von der in Fig. 4 dargestellten
Anordnung Gebrauch machen; hier ist F die Gleitfläche,
welche durch eine in einen Schlitz einspielende Kurbelschiene in Bewegung gesetzt
wird. Doch bleibt die zur Wirkung kommende Länge der Kurbelschiene nicht wie beim
Ellipsographen constant, sondern sie verändert sich während der Umdrehung. Das eine
Ende der Kurbelschiene K ist nämlich mit einem auf ihre Längsrichtung
senkrechten Führungsschlitze versehen, in welcher eine zweite durch das Zahnrad z1 in Bewegung gesetzte
Kurbelschiene K1
einspielt; sie ist in dem verticalen Zapfen z2 dieses Rades Angesetzt, welches sich an einem
feststehenden und mit ihm gleich grossen Rade z
abwälzen kann. Wird nun mit dem Griffe A der Zapfen B in der Nabe des feststehenden Rades z zur Umdrehung gebracht, so kommt, weil das untere
Ende des Zapfens B die Kurbelschiene K mit einem Führungsstücke D aufnimmt, letztere in
Umdrehung und gleichzeitig, weil sich das Rad z1 am feststehenden Rade z abwälzt, auch die Kurbelschiene K1 zur Wirkung, wobei sich die Kurbelschiene K in ihrem Führungsstücke D verschieben muss. Der Arm E, der die Hülse
des Zapfens z und die Scheibe S trägt, ist mit dem Zapfen B fest verbunden.
Die Scheibe S dient zur Uebertragung der Bewegung auf
die Zirkelschiene und zwar in dem Uebersetzungsverhältnisse = 1.
Nach einer Drehung der Kurbelschiene K um den Winkel φ wird auch die Kurbelschiene
K1 vermöge der
Gleichheit der Zahnräder z und z1 um den Winkel φ verdreht und demnach, wenn ihre zur Wirkung kommende Lange r ist, um die Strecke r sin
φ nach einwärts gezogen, so dass das Stück
aO=R-r\,sin\,\varphi, somit
ab=(R-r\,sin\,\varphi)\,sin\,\varphi ist, wobei die Länge der
Kurbelschiene K gleich R
angenommen wurde. Mit der Drehung der Kurbelschiene K
dreht sich gleichzeitig auch die Zirkelschiene von einer mit der Kurbelschiene K gleichen Lange R um den
Winkel φ und es käme der Stift, welcher sich an ihrem
Ende befindet, bei in Ruhe befindlicher Unterlagsfläche auf dem Punkt a zu stehen. Da aber die Unterlagsfläche während der
Drehung um den Winkel φ um das Stück
ab=(R-r\,sin\,\varphi)\,sin\,\varphi nach rückwärts
verschoben wurde, so wird der Stift auf einen Punkt b1 treffen, der um die Strecke a1b1 = vor dem Punkte a1 liegt. Nimmt man den
Punkt O1, der vom
Mittel-Punkte O1 der
Zirkelschiene um das Stück O_1\,O_2=r entfernt liegt, als
Ursprung eines rechtwinkligen Coordinatensystemes an, so ist
b_2\,O_1=y die Ordinate und O_2\,b_3=x die
Abcisse des Punktes b1
der vom Stifte beschriebenen Curve. Nun ist
b_1b_2=b_3O_1=R\,sin\,\varphi-(R-r\,sin\,\varphi)\,sin\,\varphi=r\,sin^2\varphi
und O_2b_3=O_1O_2-O_1b_3=x=r\,cos^2\varphi;
O_1b_2=y=R\,cos\varphi. Durch Elimination von φ erhält man die Gleichung einer Parabel, nämlich
y^2=\frac{R^2}{r}\,x.
Dieser Apparat beschreibt nur dann Parabeln, wenn Zirkelschiene und Kurbelschiene auf
dieselbe Länge eingestellt sind; andernfalls bezeichnet er Curven, deren Gleichung
vom vierten Grade ist. Ebenso ist leicht einzusehen, dass dieser Apparat nur zum
Verzeichnen von sehr flachen Parabelbögen geeignet wäre. Brächte man an der
Kurbelschiene K, wenn sie auf die vorbeschriebene Art
in Bewegung versetzt wird, einen Stift an und liesse denselben auf fester
Unterlagsfläche Curven beschreiben, so würden letzteren die Polargleichung
\varrho=(R\pm r\,sin\,\varphi) zukommen, weshalb sie auch zur
Darstellung der Schieberbewegung geeignet sein würden.
Schliesslich sei noch erwähnt, dass zum Verzeichnen von Ellipsen auch der in Fig. 8
angegebene Apparat verwendet werden könnte, welcher eine Umkehrung der früher (1877
226 237) gegebenen Ellipsographen-Anordnung
darstellt. Wird nämlich wie in Fig. 8 die Unterlagsfläche
F durch zwei Kurbeln K
von gleicher Länge in einem Kreise geschwungen (die Kurbelwarzen spielen jedoch hierbei nicht
in einem Schlitze, sondern sind in die Unterlagsfläche F eingesetzt) und der an einem Querlineale QQ
befindliche Stift S durch eine an die
Verbindungsschiene der beiden obern Kurbeln K1 aufgesetzte Warze w
in geradlinige Schwingung versetzt, so beschreibt der Stift S auf der Unterlagsfläche Ellipsen. Mit LL
ist eine der Schienen bezeichnet, an welchen das mit einem Schlitze versehene
Querlineal QQ geführt wird.
Tafeln