| Titel: | Selbstregistrirender Festigkeitsapparat von Wilh. Ritter, Professor am Polytechnicum zu Riga. |
| Fundstelle: | Band 229, Jahrgang 1878, S. 518 |
| Download: | XML |
Selbstregistrirender Festigkeitsapparat von
Wilh. Ritter, Professor
am Polytechnicum zu Riga.Vom Verfasser gef. eingesendeter Abdruck aus der Riga'schen
Industriezeitung, 1878 S. 123.
Mit Abbildungen auf Tafel 42.
Ritter's Festigkeitsapparat.
Im Blick auf die wichtige Stellung, welche die Metalle gegenwärtig auf dem ganzen
Gebiete der Technik und Industrie einnehmen, ist es nicht zu verwundern, daſs die
Natur derselben – und hauptsächlich diejenige des Eisens – mit groſsem Eifer und mit
vielem Scharfsinn studirt wird. Eine hervorragende Bedeutung besitzen in dieser
Beziehung die von Wähler angestellten Versuche, welche
die Bestimmung der Festigkeit von gespannten, gebogenen und gedrehten Metallstäben
bei häufig wiederholter Beanspruchung zum Zweck haben. Doch auch das in letzter Zeit
in umfassenderer Weise vorgenommene Studium der Elasticitätsverhältnisse ist von
hohem Werthe und ertheilt manchen Aufschluſs über die innere Natur der Metalle.
Bekanntlich hat Prof. Thurston eine längere Reihe von
Versuchen über die Torsionsfestigkeit verschiedener Materialien angestellt (vgl.
*1875 216 1. 218 185. 1876 220 193) und zu diesem Zweck einen Apparat benutzt,
welcher den Zusammenhang zwischen dem Drehungsmoment und dem Drehungswinkel
automatisch registrirt. Im Nachfolgenden soll ein Apparat beschrieben werden,
welcher im Princip denselben Zweck verfolgt, indem er den Zusammenhang der
spannenden Kraft mit der elastischen Verlängerung bei auf Zug beanspruchten Drähten
selbstthätig verzeichnet.
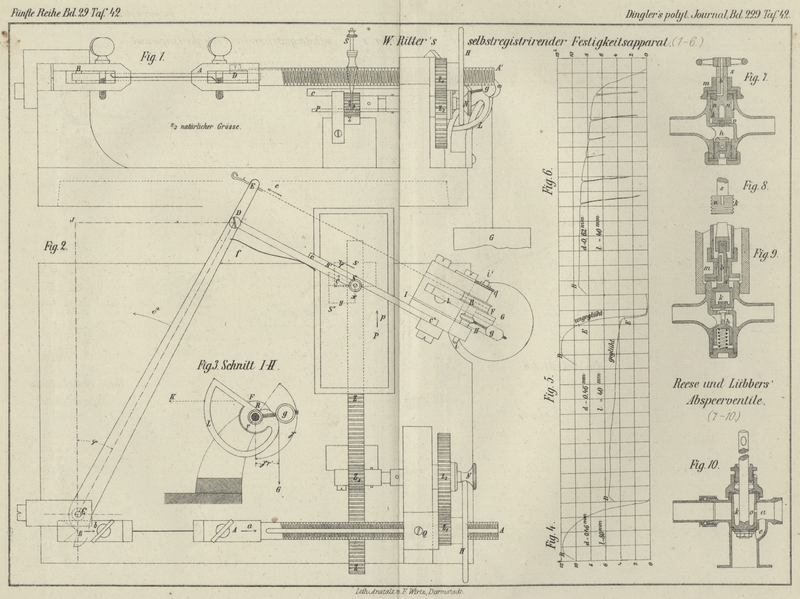
Der Apparat ist in Fig. 1 bis
3 Taf 42 in ⅔ n. Gr. dargestellt. Der zu untersuchende Draht wird in zwei
Klemmen A und B
eingespannt und durch Drehen des Handrädchens H,
welches zugleich die Mutter zu der Schraube AA'
enthält, angespannt. Damit letztere sich, nicht um ihre Längsachse drehe, ist sie
der Länge nach mit einer Nuth versehen, in welche das Schräubchen Q eingreift.So weit
ist der Apparat dem von Prof. E. Hoyer
construirten (vgl. *1875 218 191) nachgebildet.
Alles Uebrige ist indeſsen neu hinzugekommen, so namentlich die Messung der
Spannkraft und die selbstthätige Registrirung.
Um die ausgeübte Zugkraft zu messen, liegt die Klemme B
mit einer Schneide an dem kurzen, eingekerbten Arm eines um C drehbaren Winkelhebels BCE an, an dessen
längerem Arm eine feine Kette EF befestigt ist, welche
in der Weise mit einem Gewichte in Verbindung steht, daſs ihre Spannung proportional
der Drehung des Winkelhebels zunimmt. Im Punkte D ist
(bei mittlerer Lage des Winkelhebels unter rechtem Winkel) ein Seitenstab befestigt,
der in S den Schreibstift trägt; letzterer wird durch
eine kleine Feder f an eine feste Bahn cc' angedrückt und bewegt sich daher stets in gerader
Linie.
Während man das Rädchen H dreht, wird mittels der
Zahnräder Z1 bis Z3, von welchen das
erstere mit H fest verbunden ist, die geradlinig
geführte Zahnstange Z in Bewegung gesetzt und hierdurch
die mit ihr vereinigte Platte P, auf welcher das Papier
durch einen einfachen übergeschobenen Rahmen befestigt wird, in der Richtung des
aufgezeichneten Pfeiles, d.h. senkrecht zu AB,
verschoben. Es ist hiernach klar, daſs die vom Stifte S
verzeichnete Linie die relative Bewegung desselben gegenüber der Platte P angibt, und die Verhältniſse sind nun so gewählt,
daſs diese Curve in ihren Abscissen, zehnfach
vergröſsert, die Ausdehnung des Drahtes und in ihren
Ordinaten nach einem bestimmten Maſsstabe die spannende Kraft darstellt. (Die Abscissen sind hierbei
parallel der Bewegungsrichtung der Platte P, die
Ordinaten senkrecht dazu gemessen.)
Um dies zu erkennen, denken wir uns, das Rädchen H mache n Umdrehungen.
Dann verschiebt sich die Klemme A., wenn die Schraube
AA' emm Ganghöhe
hat, um a = nemm nach rechts. Da das Zahnrad Zl 24, das Rad Z2 72 Zähne hat, so
macht letzteres in derselben Zeit ⅓n Umdrehungen. Nennt
man u den Umfang des Zahnrades Z3, so verschiebt sich demnach die Platte
um p=\frac{nu}{3}, oder da n=\frac{a}{e} ist,
um p=\frac{au}{3e}. Das Zahnrad Z3 hat nun 15 Zähne, und die Zahndistanz auf der
Zahnstange Z beträgt 2mm; folglich ist u=30^{mm}. Ferner ist der
Schraubengang e=1^{mm}; somit ergibt sich
p=10^a.
In derselben Zeit dreht sich der in der Zeichnung in mittlerer
Lage dargestellte Winkelhebel BCD um δ in der durch einen Pfeil angegebenen Richtung. Dann
bewegt sich die Klemme B in der Richtung gegen A hin um
b=BC \times sin\,\,\delta, der Stift S gleitet längs der Bahn cc' um s=CD
\times sin\,\,\delta gegen D hinGenau genommen ist s etwas gröſser, da D sich in einem Kreisbogen bewegt, S aber längs einer Geraden gleitet; der
begangene Fehler ist indeſsen, da der Winkel δ
höchstens zwischen + 7° und – 7° schwankt, verschwindend klein.;
es ist demnach s=\frac{CD}{BC}\,b.
Die Linie, welche der Stift S
beschreibt, finden wir nun folgendermaſsen. Während sich S nach S' (Fig. 2)
bewegt, gleitet die Platte P um die Strecke
S'S''=p unter dem Stift weg; letzterer gelangt also auf dem
Papier nach S''. Bezieht man nun den Punkt S'' durch die Coordinaten x und y auf den Ausgangspunkt S, bezeichnet den Winkel JCD mit φ und berücksichtigt, daſs DS auf CD senkrecht steht,
so wird x=p-s\,sin\,\varphi. oder nach Einführung der für p und s gefundenen Werthe
x=10\,a-\frac{CD}{BC}\,b\,sin\,\,\varphi. Nun ist aber
CD\,sin\,\,\varphi=DJ, folglich
x=10\,a-\frac{DJ}{BC}\,b. Da DJ=80^{mm},
BC=8^{mm} ist, so folgt endlich:
x=10\,(a-b); . . . . . . . . (1)
a-b ist aber die wirkliche
Ausdehnung des Drahtes; folglich gibt x, wie behauptet
wurde, die zehnfache Ausdehnung an.
Zweitens wird die Ordinate der Curve
y=s\,cos\,\varphi; bezeichnet man die Verschiebung des
Punktes E in der Richtung FE mit e, so verhält sich
s:e=CD:CE, oder es ist
y-\frac{CD}{CE}\,e\,cos\,\varphi, oder, da
CD\,cos\,\varphi=CJ:
y=\frac{CJ}{CE}\,e . . . . . . . . (2)
Die Ordinate y ist somit der
Verschiebung des Punktes E proportional, und damit sie
die im Drahte wirkende Kraft repräsentire, muſs die in der Kette EF herrschende Spannung so regulirt werden, daſs sie
der Gröſse e proportional bleibt.
Zu diesem Zweck ist die Kette um eine cylindrische Rolle R (Fig. 3)
geschlungen, welche nebst einer (durchbrochenen) Spiralscheibe L auf einer kleinen Achse ii' (Fig. 2)
befestigt ist. Ueber die Spiralscheibe ist eine Schnur gelegt, an deren unterem Ende
ein Gewicht G hängt, welches offenbar der in der Kette
herrschenden Zugkraft entgegenwirkt. Die Spirale ist eine Kreisevolvente, d.h. sie
ist durch Abwicklung eines um einen Kreis geschlungenen Fadens entstanden; daraus
folgt, daſs der Hebelarm, an welchem das Gewicht G
wirkt, proportional der Drehung der Achse ii', also in
der That proportional der Gröſse e zunimmt.
Um den Maſsstab zu finden, in welchem der Schreibstift die im
Drahte wirkende Kraft aufträgt, bezeichnen wir den Radius des Kreises, dessen
Abwicklung die Spirale ergeben hat, mit r', den Radius
der Rolle R mit r, den
Drehungswinkel der Achse ii' (von der Nulllage aus
gerechnet) mit y, die Spannung in der Kette mit K und die im Drahte wirkende Kraft mit T. Dann ist zunächst der Hebelarm des Gewichtes G gleich yr'; denn
derselbe nimmt proportional der Drehung zu und ist nach einer Drehung um 360° gleich
2πr'; d.h. gleich dem Umfang des abgewickelten
Kreises. Es besteht somit, da K beständig am Hebelarm
r angreift, die Gleichheit der statischen Momente
G\,\gamma \,r'=R\,r, woraus R=\frac{G\,\gamma
\,r'}{r}.
Da ferner R und T (mit verschwindendem Fehler) an den Hebelarmen
CE \times cos\,\delta, bezieh. BC \times
cos\,\delta angreifen, so ist weiter:
R \times CE \times cos\,\delta = T \times BC\,cos\,\delta,
oder
T=\frac{CE}{BC}\,R = \frac{CE \times G\,\gamma\,r'}{BC \times r},
woraus
\gamma=\frac{BC \times rT}{CE \times r'G}.
Während sich die Achse ii' um den
Winkel y dreht, wickelt sich aber die Kette um die
Strecke e=\gamma r ab: wir können somit an Stelle von Gleichung
(2) setzen: y=\frac{CJ}{CE}\,\gamma\,r, oder nach Einsetzung
obigen Ausdruckes für γ:
y=\frac{CJ \times BC \times r^2}{CE^2 \times r'G}\,T. . . . . . .
. . . . (3)
Diese Gleichung stellt das Verhältniſs der Ordinate y zu der Drahtspannung T
dar. Durch zweckmäſsige Wahl des Gewichtes G kann man
dieses Verhältniſs nach Belieben gestalten. Soll z.B. jedes Millimeter von y ein Kilogramm darstellen, so muſs der Factor von T = 1 sein, oder es ist:
G=\frac{CJ \times BC \times r^2}{CE^2 \times r'} . . . . . . . .
. . (4)
zu machen. In der Ausführung ist CJ=150^{mm},\
BC=8^{mm},\ r=8^{mm},\ CE=190^{mm} und
r'=4^{mm},61; folglich muſs in diesem Fall
G=0^k,461 sein.
Da der Papierstreifen bis zu einer Breite von 35mm
befahren werden kann, so ermöglicht dieses Gewicht das Messen von Spannungen bis zu
35k. Doch läſst sich bei so groſsen Kräften
der Draht nicht mehr sicher einspannen; auch wird es sehr schwierig, das Handrädchen
R zu drehen. Die Versuche sind deshalb stets mit
geringern Spannungen ausgeführt worden, und stehen zu diesem Behufe Gewichte von ⅘,
⅖ und ⅕ des obigen Werthes zur Verfügung, so daſs dann in dem verzeichneten
Diagramme jedes Millimeter der Ordinate 0,8, 0,4, bezieh. 0k,2 repräsentiert.
Die Papiere, auf welchen die Curve (Fig. 4 bis
6) verzeichnet wird, sind durch Quer- und Längslinien in Quadrate von
5mm Seite eingetheilt, so daſs sowohl die
Verlängerung des Drahtes, als auch die spannende Kraft leicht abgelesen werden kann.
Bezüglich der letzteren stellt ein Theilstrich je nach dem angehängten Gewichte 1,
2, 4 oder 5k dar.
Es ist noch darauf aufmerksam zu machen, daſs beim Einspannen eines neuen Drahtes der
Zusammenhang zwischen dem Handrädchen H und der Platte
P gelöst werden muſs, was durch leichtes Drehen des
Schraubenknopfes N, welcher sonst das lose aufgesteckte
Zahnrad Z2 anpreſst,
rasch geschehen kann. Ferner ist noch zu bemerken, daſs sich an dem hintern Ende der
Achse ii' ein kleines auslösbares Sperrrädchen q befindet, wodurch ein schädliches Herunterfallen des
Gewichtes G vermieden wird.
Endlich sei noch erwähnt, daſs die Spiralscheibe, damit sie nicht in Folge ihrer
unsymmetrischen Gestalt ein schädliches Drehmoment auf die Achse ii' ausübe, mit einem kleinen verstellbaren
Gegengewicht g versehen ist, welches ihrem Schwerpunkt
gegenüber liegt.
Der vom Verfasser benutzte Apparat ist vom Mechaniker Franz in Riga ausgeführt worden und arbeitet, abgesehen
von kleinen Störungen, die sich nach einiger Uebung leicht beseitigen lassen, mit
überraschender Regelmäſsigkeit. Indessen wäre zu wünschen, daſs derselbe von
vornherein in gröſserem Maisstabe angefertigt worden wäre, damit die unvermeidlichen
Reibungseinflüsse weniger ins Gewicht fallen und stärkere Drähte als blos solche von
0,5 bis 0mm,7 Dicke geprüft werden könnten. Auch
erfüllen die Klemmen ihren Dienst bei stärkeren Spannungen nur unvollkommen, indem
sie bei glatter Oberfläche den Draht leicht rutschen lassen, bei rauher Oberfläche
dagegen denselben zuweilen an der Einspannstelle zu stark quetschen. Gegenwärtig
besitzen sie eine kleine Längsrille und wirken befriedigend.
Der Apparat ist zunächst zu Demonstrationen in Vorlesungen
bestimmt; in welcher Weise und in welchem Umfange er zu praktischen Versuchen (sei
es auf dem Gebiete der Metall- oder der Textilindustrie) benutzt werden kann, mag
die Zukunft lehren. Jedenfalls besitzt derselbe zwei wesentliche Vorzüge: er
ermöglicht ein sehr rasches Experimentiren und liefert die Resultate vollständig
unabhängig von jeglichen Beobachtungsfehlern.
Um die Wirksamkeit des Apparates zu illustriren, sind in Fig.
4 bis 6 einige
Proben von Diagrammen, genau nach den Originalen copirt, aufgenommen worden, und
zwar in natürlicher Gröſse. Die (nach links positiven) Horizontalen stellen die
zehnfachen Verlängerungen, die Ordinaten die Spannungen (im Maſsstab 1mm = 0k,4)
dar.
Fig.
4 zeigt zunächst das Diagramm für einen Eisendraht von 0mm,46 Durchmesser und 80mm Länge. Die Curve beginnt mit einer schwachen
Concaven, welche wahrscheinlich gröſstentheils der ersten Geradstreckung
zuzuschreiben ist.Nach den von Prof. Bauschinger angestellten
Experimenten zeigen die Diagramme auch bei der gröſsten Genauigkeit stets
eine anfängliche Concavität, und findet dieselbe offenbar in der Natur der
Metalle ihren Grund; bei den vorliegenden Curven haben indeſsen jedenfalls
beide Factoren mitgewirkt und dürfte es schwierig sein, zu entscheiden, wie
viel auf Rechnung des einen und 'wie viel auf Rechnung des andern zu setzen
ist. Dann steigt sie ziemlich geradlinig und steil an, biegt sich
hierauf langsam herum, wird flacher und endigt im Punkte B, welcher die Bruchstelle bezeichnet. (Der Stift springt an der
Bruchstelle stets ein wenig zurück, wodurch der kleine, abwärts gerichtete Strich
entsteht, der natürlich mit dem Wesen der Curve nichts zu thun hat.) Die Festigkeit
des Drahtes findet sich gleich 11k,8, die
Verlängerung bis zum Bruch gleich 1mm,7. Die
Elasticitätsgrenze liegt da, wo die Linie sich zu krümmen anfängt, ist indeſsen im
vorliegenden Beispiel nicht genau erkennbar. Der Elasticitätsmodul lieſse sich aus
der anfänglichen Neigung der Curve berechnen, jedoch nur angenähert.
Um den Einfluſs zu zeigen, welchen das Ausglühen eines Drahtes auf
seine Festigkeit und Elasticität ausübt, wurden in Fig. 5 zwei
Eisendrähte von gleichem Durchmesser und gleicher Länge, jedoch der eine in
geglühtem. der andere in ungeglühtem Zustande, behandelt. Der Unterschied bezüglich
der Festigkeit sowohl, als bezüglich der Dehnbarkeit ist überraschend groſs; erstere
ist durch das Ausglühen ungefähr auf die Hälfte herabgesunken, letztere dagegen
beinahe auf das Fünffache gestiegen. Die Elasticitätsgrenze ist hier besser
erkennbar- sie befindet sich ungefähr da, wo der Buchstabe E steht.
In Fig. 6 ist
ein etwas dickerer, ausgeglühter Draht wiederholt angespannt worden. Es entsteht
hierbei der schon von Thurston construirte Linienzug.
Der zurückgehende Stift beschreibt stets eine Gerade, aus deren unterem Ende die
bleibende Verlängerung des Drahtes zu ersehen ist. Bei der Neuanspannung verfolgt
der Stift dieselbe Gerade bis fast an ihr oberes Ende und lenkt dann mit schwacher
Abbiegung wieder in die alte Bahn ein. Die Elasticitätsgrenze (welche, wie gesagt,
da anzunehmen ist, wo die Curve aus der geraden Richtung in die krumme überzugehen
beginnt) rückt, wie aus diesem Diagramme zu ersehen ist, bei jeder neuen Anspannung
etwas höher hinauf. Aus dem Umstände, daſs sich der Stift auf den verschiedenen
Zwischenbewegungen in paralleler Richtung bewegt, ist zu schlieſsen, daſs sich der
Elasticitätsmodul während dieser Behandlung nicht wesentlich geändert hat.
Tafeln