| Titel: | Ueber den Regulir- und Absperrapparat mit indirecter Uebertragung für hydraulische Motoren. Dr. R. Proell's Patent. |
| Fundstelle: | Band 231, Jahrgang 1879, S. 108 |
| Download: | XML |
Ueber den Regulir- und Absperrapparat mit
indirecter Uebertragung für hydraulische Motoren. Dr. R. Proell's Patent.
Mit Abbildungen auf Tafel 11.
(Fortsetzung von S. 20 dieses Bandes.)
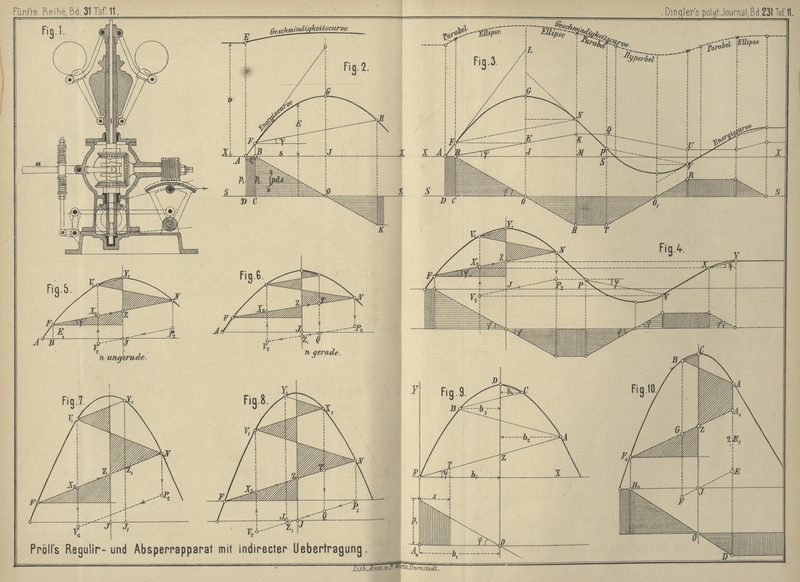
Pröll's Regulir- und Absperrapparat.
Theorie des Apparates und der durch
ihn veranlaſsten Regulirung des hydraulischen Motors. Theoretisches
Regulirungsdiagramm.
Wir machen in der Folge die Annahme, daſs die Veränderung der bewegenden Kraft durch
den Apparat proportional dem vom rotirenden Massentheilchen im Abstande R der Hauptwelle zurückgelegten Wege s sei.
Je gröſser die Gefällhöhe der den Motor beaufschlagenden Wassermasse und je niedriger
die Höhe dieser ist, desto mehr stimmt diese Annahme mit der Wirklichkeit überein. Aber sie erscheint
auch für die thatsächlich vorkommenden Höhen der Gefälle und beaufschlagenden
Wassermassen anwendbar, wenn wir berücksichtigen, daſs eine genaue Feststellung des
Gesetzes, wie sich die das Massentheilchen beschleunigende Kraft mit dem Wege
ändert, nur in einzelnen Fällen möglich sein und sich jedesmal nach der speciellen
Construction der Wasserzuführungstheile am hydraulischen Motor richten wird. Und
dann auch werden sich der Bestimmung dieses Gesetzes erhebliche Schwierigkeiten in
den Weg stellen, da der Nutzeffect des hydraulischen Motors wesentlich von der
Gefällhöhe und der Menge der beaufschlagenden Wassermassen abhängig ist und dieser
doch bei der Bestimmung der effectiven, auf die Hauptwelle kommenden und die träge
Masse des hydraulischen Motors beschleunigenden Kraft berücksichtigt werden muſs.
Andererseits lehrt aber auch die einfache Anschauung, daſs an Stelle der von uns
angenommenen und der Proportionalität zwischen Kraft und Weg entsprechenden geraden
Linie in WirklichkeitWirklichkait eine nur sehr flache, gekrümmte Curve treten wird, die insbesondere den
weiteren Verlauf des theoretischen Regulirungsdiagrammes im Princip nicht ändern
wird.
Wir nehmen nun ferner an, der Apparat befinde sich in seiner mittleren Stellung, d.h.
der Regulator halte die Kupplungshülse in der Mitte, also auſser Eingriff, der
Schützen stehe demnach still und der Motor arbeite mit der halben Maximalkraft.
Bezeichnen wir die der höchsten Stellung des Schützen, also der vollen
Beaufschlagung entsprechende Anzahl Pferdestärken mit Nm, so würde also der Motor bei mittlerer
Stellung des Schützen mit N_1=\frac{N_m}{2} Pferdestärken
arbeiten.
In Fig.
2 Taf. 11 bezeichne die Abscissenachse XX den
rectificirten Weg des rotirenden Massentheilchens; es werde nun bei A Widerstand ausgerückt. Die dabei für jede
Masseneinheit frei werdende beschleunigende Kraft p1, sei durch die Ordinate AD dargestellt. Die bis dahin constante Geschwindigkeit v des Motors, welche durch eine der X-Achse parallel gehende gerade Linie dargestellt
werde, nimmt zu, so daſs im Diagramm von F ab eine
Curve aufsteigt. In Folge dieser Geschwindigkeitsvermehrung im Gange des Motors
veranlaſst der Regulator eine Hebung der Kupplungshülse im Apparat und führt,
nachdem er eine hinreichend starke Friction erzeugt hat, bezieh. die Zähne in der
Kupplung zur Berührung gelangt sind und der todte Gang in der Zahnradübertragung und
dem Hebelwerk nach dem Schützen überwunden worden ist, ein Zuschützen herbei;
dadurch wird die bewegende Kraft gemäſs unserer oben motivirten Annahme proportional
dem Wege verkleinert.
Die gerade Linie, welche diese Verminderung im Diagramm anzeigt, schneidet
schlieſslich die X-Achse im Punkte O, die bis dahin erhaltene Fläche der aufgesammelten lebendigen Kraft setzt
sich wie aus der Figur ersichtlich aus einem (vertical schraffirten) Rechteck und
(horizontal schraffirten) Dreieck zusammen. Ueber dem Rechteck erscheint als
Geschwindigkeitscurve ein Parabelbogen und über dem Dreieck der positiven lebendigen
Kraft eine Ellipse, welche Curven beide tangential in einander übergehen.
Wir stellen uns nun die Aufgabe, in das Diagramm die durch die
Geschwindigkeitsänderung im Regulator hervorgerufene Energie ebenfalls als Curve
einzutragen. Zu dem Ende setzen wir voraus, der Apparat sei mit einem Regulator
unseres verbesserten patentirten Systemes versehen, wie derselbe in D. p. J. * 1878 227 13. 113. 216 beschrieben ist. Der
daselbst gegebenen Theorie entnehmen wir die Gleichung:
E=2\,hP\,\left(\frac{\omega^2-{\omega_0}^2}{g}\right),. . .
. . . . . (1)
worin ω0 die normale Winkelgeschwindigkeit der Regulatorspindel ω deren vermehrte
Geschwindigkeit (\omega>\omega_0), P
das Kugelgewicht, g die Beschleunigung der Schwere, h eine aus dem Mechanismus des Regulators leicht
abzugreifende geometrische Strecke und E die bei der
Vermehrung der Geschwindigkeit ω0 auf ω in der
Regulatorhülse auftretende Energie bedeutet.
Sind Ω0 und Ω die den Werthen ω0 und ω entsprechenden
Winkelgeschwindigkeiten der Hauptwelle des Motors, so ist \Omega
R=v der Peripheriegeschwindigkeit des Massentheilchens m, welches durch die bewegende Kraft p in beschleunigte Geschwindigkeit versetzt wird, u die Tourenzahl der Regulatorspindel in der Minute,
U diejenige des hydraulischen Motors, so ist
\frac{\omega}{\Omega}=\frac{u}{U}, also folgt:
\omega=\frac{u}{U}\,\Omega oder
\omega=\frac{u}{U}\,\frac{v}{R}. . . . . . . . . (2)
Setzen wir diesen Werth in Gleichung (1) ein, so folgt:
E=\frac{2\,Ph}{g}\,\frac{u^2}{U^2}\,\frac{1}{R^2}\left(\frac{v^2-{v_0}^2}{2}\right).
. . . . (3)
oder setzen wir das Product:
\frac{2\,Ph}{g}\,\frac{u^2}{U^2}\,\frac{1}{R^2}=\frac{1}{l},
. . . . . (4)
so folgt:
E=\frac{1}{l}\left(\frac{v^2-{v_0}^2}{2}\right). . . . .
(5)
Nach dem Princip der lebendigen Kräfte ist aber allgemein:
\frac{v^2-{v_0}^2}{2}=\int\limits_0^sp\;ds. .
. . . . (6)
somit ist:
E=\frac{1}{l}\int\limits_0^sp\;ds. . . . . . .
. . . (7)
Hat das Massentheilchen m in Fig.
2 den Weg s zurückgelegt, so ist das Integral
\int\limits_0^sp\;ds der Inhalt der Fläche über dem Wege s, welche die aufgesammelte lebendige Kraft darstellt.
Dabei ist es gleichgiltig, ob der Grenzwerth s <
oder > DO ist. Da nun, wie leicht ersichtlich,
von O ab die in ihrer Richtung weiter laufende gerade
Linie BO die hinfort verzehrte lebendige Kraft
darstellt, so folgt der wichtige Satz: Die Energie des
Regulators ist proportional der Arbeitsfläche der aufgesammelten bezieh.
verzehrten lebendigen Kraft.
Stellen wir nun im Diagramm Fig. 2 die
Veränderung der Energie E des Regulators durch eine
Curve dar, die von A beginnt, deren Abscissen also in
der Achse XX liegen, so ist leicht einzusehen, daſs
nach obigem Satze im Diagramm über dem Rechteck bezieh. Dreieck der lebendigen
Kräfte als Energiecurve eine gerade Linie bezieh. eine Parabel erscheinen
wird, deren Achse die durch O gezogene Verticale ist.
Die gerade Linie, mit welcher die Energiecurve beginnt, ist gleichzeitig Tangente an
den Parabelbogen.
Bezüglich des Gesetzes, nach welchem sich die Spannungen der Federn auf der
Auslösungsstange mit dem Ausschlag des Zahnsectors im Apparat ändern, nehmen wir an,
daſs diese Spannungen proportional der Verstellung des Schützen zu- bezieh.
abnehmen. Es ist diese Annahme zulässig, da wir die Verschiebung der
Auslösungsstange in Folge der mäſsigen Ausschläge des Zahnsectors und des
Hebelwerkes proportional der Schützenbewegung setzen können.
Combiniren wir diese Annahme mit unserer früheren, daſs auch der Schützen
proportional dem Wege s des rotirenden Massentheilchens
bewegt werde, so folgt, daſs wir die Veränderung der
auf die Kupplungshülse reducirten Federspannungen T
ebenfalls durch eine gerade Linie darstellen können,
welche gegen die X-Achse um einen bestimmten. Winkel geneigt ist. Diese Gerade der
Federspannungen würde überall da erscheinen, wo auch die Verstellungsgerade des
Schützen ist. Erstere beginnt im Punkte F. Der Winkel,
den sie mit der X-Achse einschlieſst, ist um so
gröſser, je stärker die Federn sind.
Das Diagramm zeigt nun, daſs die ansteigende Gerade der Federspannungen im Punkte H die Energiecurve schneidet, weil in Folge der
fortgesetzten, noch über O hinaus währenden Verstellung
des Schützen die Energiecurve, nachdem sie über O,
entsprechend dem Maximum von angesammelter lebendiger Kraft, in G ihren höchsten Punkt erreicht hat, sich wieder der
Abscissenachse nähert, während die Gerade der Federspannungen sich von derselben
noch weiter entfernt. Somit müssen sich beide schneiden. Tritt dies ein, so heilst
dies, die mit der Verstellung des Schützen wachsende
Federspannung ist gleich der Energie des Regulators geworden. Der
Regulator kann in seiner obersten Lage nun nicht mehr verbleiben. Unter dem Einfluſs
der wachsenden Federspannung wird die Kupplungshülse ausgerückt und die fortgesetzte
Verstellung des Schützen eingehalten.
Die Ordinaten der Energiecurve über dem Anfangsweg AB
stellen Energiewerthe dar, welche gewissermaſsen für die Regulirung verloren gehen,
da die Verstellung des Schützen erst im Punkte B statt
in A beginnt. Wir nennen daher die gröſste Ordinate BF den Energieverlust und setzen
denselben = E1.
Derselbe setzt sich aus mehreren Gröſsen zusammen, zunächst aus dem Energieverlust
E0, welcher daher
rührt, daſs in Folge von nicht zu vermeidenden Reibungen der Regulator nach
erfolgter Geschwindigkeitsänderung nicht sofort die Kupplungshülse aus- bezieh.
einrückt und sich erst ein wenig Energie E0 ansammeln muſs, bevor diese schädlichen Reibungen
überwunden sind, ferner aus dem Energieverlust E2, daher rührend, daſs einerseits bei dem
Frictionswendegetriebe erst die Energie des Regulators bis zu dem für die Bewegung
des Schützen nothwendigen Frictionsdrucke anwachsen muſs, andererseits bei der
Zahnkupplung (namentlich wenn nur ein Mitnehmerzahn vorhanden ist) todter Gang
vorhanden ist.
Mag E2 in diesem oder
jenem Falle auch wesentlich verschiedene Werthe annehmen, so wird man doch allgemein
E_1=E_0+E_2 setzen können. Nach der allgemeinen Gleichung (7)
ist nun:
E_1=E_0+E_2=\frac{1}{l}\int\limits_0^{s_1}p\;ds . . .
(8)
worin s1 = AB (Fig. 2) ist.
Nun ist aber \int\limits_0^{s_1}p\;ds gleich dem Inhalt des
Rechteckes ABCD, welchen wir mit
\frac{J}{2} bezeichnen wollen, also folgt
J=2\,l(E_0+E_2). . . . . . . . . . . (9)
oder allgemein, wenn wir für l
den Werth aus Gleichung (4) einsetzen:
J=\frac{g}{Ph}\,\frac{U^2}{u^2}\,R^2\,(E_0+E_2). . . . .
(10)
Weiter ergeben sich für die die Masseneinheit beschleunigende Kraft p folgende Beziehungen.
Ist N die Anzahl der in der Peripherie des Kreises R (Riemenscheibenumfang u.s.w. in Meter gemessen) an
der Hauptwelle auftretenden Pferdestärken, so ist bekanntlich die Umfangskraft K nach der Gleichung bestimmt:
K=\frac{716,2\,N}{UR}. . . . . . . . . . . . .
. . . (11)
Nun ist, wenn M die gesammte auf den erwähnten Kreis
reducirte, in Rotation
befindliche träge Masse des Motors mit der daran hängenden Transmission den nicht
ausgerückten Arbeitsmaschinen u.s.w. bedeutet:
p=\frac{K}{M}, also auch
p=\frac{716,2\,N}{URM}. . . (12)
Bezeichnen wir im Speciellen mit p1 die im Punkte A
auftretende bewegende Kraft, mit N1, die ausgerückten Pferdestärken, so folgt:
p_1=\frac{716,2\,N_1}{URM}. . . . . . . . . .
. . . . . . . (13)
Mit Hilfe der im Vorstehenden hergeleiteten Gleichungen und Beziehungen können wir
nun das theoretische Regulirungsdiagramm wie folgt construiren. Gegeben seien die
Werthe U, R, M und die ausgerückte Anzahl
Pferdestärken. Dann berechnet sich zunächst nach Gleichung (13) die bewegende Kraft
für die Masseneinheit p. Sind im Weiteren für den
Regulator die Werthe P, h, u gegeben und für E0 und E2 bestimmte Werthe
angenommen, so berechnet sich nach Gleichung (10) der Werth J. Da nun \frac{J}{2}=\int\limits_0^{s_1}p\;ds=p_1s_1
gesetzt wurde, so folgt:
s_1=\frac{J}{2\,p_1}. . . . . . . . . . . . .
. . . . . . . . (14)
Der Weg s0
– s1, welchen das
rotirende Massentheilchen von A bis zum Punkte J zurücklegt, ergibt sich aus der totalen
Verstellungszeit tm des
Apparates, wie folgt. Bezeichnet man letztere mit tm und mit v
die mittlere lineare Geschwindigkeit des Massentheilchen m, so ist angenähert (wegen der im Allgemeinen geringen
Geschwindigkeitsschwankungen):
s_m=vt_m=\frac{R\,\pi\, U}{30}\,t_m. . . . . .
. . . . . (15)
Die totale Verstellungszeit tm setzen wir für den Apparat als bekannt, bezieh. gegeben voraus;
dieselbe ist auſser durch die dem Apparat zu Grunde gelegten Dimensionswerthe auch
durch die minutliche Tourenzahl des Regulators bestimmt. Aus Gleichung (15)
berechnet sich der Werth sm. Ist Nm die Maximalpferdestärke, so ist:
\frac{N_1}{N_m}=\frac{s_0-s_1}{s_m}, also
s_0-s_1=s_m\,\frac{N_1}{N_m}. . (16)
Aus den Gröſsen p1
Gleichung (13), s1
Gleichung (14) und s_0-s_1, Gleichung (16) können wir nun die
Fläche der angesammelten lebendigen Kraft verzeichnen; die Verstellungsgerade des
Schützen schlieſst mit der Abscisse einen Winkel φ ein,
welcher sich aus der Gleichung tg\,\varphi=\frac{p_1}{s_0-s_1}
bestimmt.
Zur Construction der Energiecurve bestimmen wir zunächst nach Gleichung (4) den Werth
\frac{1}{l}=\frac{2\,Ph}{g}\,\frac{u^2}{U^2}\,\frac{1}{R^2}.
Setzen wir denselben in die allgemeine Gleichung (7) ein, so folgt:
E=\frac{p_1s_0}{l}. Diesen Werth errichten wir als verticale
Strecke JL in J (Fig.
3). Verbinden wir AL, so muſs offenbar diese
Linie die Energiecurve über dem Wege s_0=AJ sein und nach dem
Früheren die Tangente an die von F nunmehr beginnende
Energieparabel. Nach den geometrischen Eigenschaften der Parabel gewinnen wir deren
Scheitelpunkt, wenn wir durch F eine Horizontale ziehen
und den Abschnitt LE in G
halbiren. Die Ordinate GJ stellt dann die Energie des
Regulators in der Kupplungshülse dar, wenn die Ansammlung von lebendiger Kraft ein
Maximum geworden ist.
Wir ziehen nun von B aus eine Gerade unter einem Winkel
ψ, welcher der Spannung der Feder entspricht und
durch die Gleichung:
tg\,\psi=\frac{2\,T_m}{s_m}. . . . . . . . . .
. . . (17)
bestimmt ist, wenn mit Tm die Maximalspannung der Feder bezeichnet
wird, welche eintritt, wenn der Zahnsector des Apparates von der Mitte ganz nach
rechts oder links sich umgelegt hat und demzufolge der Schützen sich in seiner
tiefsten bezieh. höchsten Lage befindet. Die Ordinate FB bedeutet im Diagramm den Energieverlust E1.
Nehmen wir nun an, in Folge desselben höre die Bewegung des Schützen um eben so viel
früher auf, als sie später angefangen hat (eine Annahme, welche bei der
Frictionskupplung streng richtig und bei der Zahnkupplung angenähert ist), so endet
im Diagramm die Verstellungsgerade des Schützen im Punkte H, wenn gerade MN-MK=E_1 geworden ist. Bis N reicht also auch nur die Energieparabel.
Jetzt beginnt die Stillstandsperiode des Schützen, gekennzeichnet durch eine von H aus parallel zur X-Achse
laufende Gerade. In N setzt sich als Fortsetzung der
Energiecurve eine Gerade an, welche Tangente an die Energieparabel ist. Nachdem im
Punkte S wieder SQ-SP=E_1 geworden
ist, beginnt wieder die Verstellung des Schützen, jetzt aber im entgegengesetzten
Sinne, dargestellt durch die Linie TO1. Ueber O1 erreicht die an P
tangential ansetzende Energieparabel ein relatives Minimum, hinter welchem die
Energieparabel wieder aufzusteigen beginnt, bis abermals die jetzt stetig sinkende
Federspannung sich der anwachsenden Energie bis auf den Energieverlust E1 genähert hat. Es
erfolgt dann abermals Ausrückung im Wendegetriebe und Stillstand des Schützen.
Das Diagramm läſst in seinem Verlauf nun schon deutlich erkennen, welchen Einfluſs
die Auslösungsvorrichtung auf die Tödtung der lebendigen Kräfte hat.
Fassen wir die Abstände der Punkte B, H und R von der Geraden SS ins Auge, so sehen
wir, daſs sich dieselben allmälig verkürzen. Die Abweichungen des Schützen von der
Geraden SS, in welche er sich schlieſslich einstellen
soll, werden immer kleiner. Da nun die Energiecurve als eine verzerrt gezeichnete
Geschwindigkeitscurve zu betrachten ist (denn die Minima und Maxima beider Curven
fallen in dieselben Verticalen), so ersehen wir aus dem Verlauf derselben, daſs auch
eine Verflachung der Geschwindigkeitswellen eintritt und daſs schlieſslich bis auf
den der Ausgleichung sich entziehenden Energieverlust E1 verhältniſsmäſsig schnell (im Diagramm
nach 1½ Geschwindigkeitswellen) ein neuer Beharrungszustand für den Motor erzielt
wird.
Die dem Diagramm zu Grunde liegende Gesetzmäſsigkeit läſst sich besonders in dem
Verlauf und der Art der einzelnen Curven erkennen.
Die Fläche der lebendigen Kräfte setzt sich aus Rechtecken und Dreiecken
zusammen, über deren Aufeinanderfolge und Gröſse im Weiteren noch eine besondere
Untersuchung angestellt werden soll.
Die Energiecurve setzt sich aus geraden Linien und Parabelbögen zusammen, und
zwar befindet sich stets über dem Rechteck der lebendigen Kraft eine gerade Strecke,
über dem Dreieck derselben ein Parabelbogen.
Die Geschwindigkeitscurve setzt sich zusammen aus
einzelnen Bögen der drei Kugelschnitte, und zwar
erscheint über dem Rechteck der lebendigen Kräfte ein
Parabelbogen und über dem Dreieck derselben ein Ellipsen bezieh. Hyperbelbogen, je nachdem
sich die Verstellungsgerade des Schützen der Geraden SS
nähert, oder sich von dieser entfernt.
Die Veränderung der Federspannungen stellt sich durch einen gebrochenen Linienzug dar.
Statt des Linienzuges BKQU.... können wir auch den in
Fig. 3 punktirten Linienzug FNPV.... wählen,
der gegen ersteren nur um den Energieverlust E1 nach oben bezieh. unten verschoben ist und sich
mit den geraden Strecken NP.... der Energiecurve deckt.
Dieser Linienzug löst sich von der Energiecurve, sobald eine Verstellung des
Schützen stattfindet und deckt sich mit ihr in den Stillstandsperioden des
Schützen.
Fig.
4 stellt dasselbe Diagramm mit Hinweglassung der Hilfslinien dar;
insbesondere ist der eben erwähnte transponirte Linienzug der Federdruckgeraden
allein eingetragen. Ferner ist angedeutet, daſs die Neigungen φ der Verstellungsgeraden, sowie die Neigungen ψ der
Federdruckgeraden, soweit dieselben nicht auf die geraden Strecken der Energiecurve
fallen, gegen die Horizontale constant sind. Es bedarf dies kaum einer Begründung,
da die Functionirung des Apparates genau in derselben Weise vor sich geht, mag
derselbe den Schützen heben oder senken.
Aus diesen und den vorhin erwähnten Eigenschaften der im Diagramm vorkommenden Curven
bezieh. Linienzüge ergibt sich folgende hoch interessante und sehr vereinfachte Construction des theoretischen Regulirungsdiagrammes.
Aus der Gleichheit der Winkel φ folgt, daſs die
Parabelbögen FN, PV und XY
sämmtlich einer Parabel angehören und daſs, wenn wir die Geraden PV und XY sich selbst
parallel und in gleicher Gröſse in das erste Parabelsegment eintragen derart, daſs
V1N ∥ PV und XY ∥ V1Y1, ist, FNV1Y1 einen gebrochenen Linienzug bildet und Bogen PV = Bogen NV1 ferner Bogen XY =
Bogen V1Y1 ist.
Statt das Diagramm in seiner ganzen Ausdehnung zu zeichnen, können wir demnach
folgende vereinfachte Construction (Fig. 5)
vornehmen: Wir verzeichnen auf Grund der früher gegebenen Beziehung die
Energieparabel mit der ersten geradlinigen und dem Energieverlust E1 entsprechenden
Anfangsstrecke AF, ziehen von F unter dem durch Gleichung (17) bestimmten Winkel ψ einen Linienzug FNV1Y1, von welchem wir
zunächst annehmen wollen, daſs er im Scheitelpunkt der Parabel endet. Bezeichnen wir
den Schnittpunkt der ersten Geraden FN mit der
Parabelachse mit Z, so ist der Abstand ZJ gleich der Entfernung der in Fig. 4 von
Y aus entsprechend dem neuen Beharrungszustand
horizontal verlaufenden Energiegeraden. Dies erhellt sofort, wenn wir in Fig.
4 die Punkte P, V, X, Y auf die durch die
Punkte N, V1 und Y1, gezogenen
Verticalen projiciren und den in Fig. 4
punktirten und mit Pfeilen besetzten Linienzug NP2V2X2 bilden. Da NP2 = V2X2 = 2 E1 ist, so muſs die verticale Projection von Y nach Z fallen. Je weiter
in Fig. 4 der Punkt Y als Anfangspunkt eines
neuen Beharrungszustandes von der Abscissenachse zu liegen kommt, desto gröſser ist
die Abweichung der neu gewonnenen Normalgeschwindigkeit von der ersten. Der Abstand
ZJ läſst also in Fig. 5
sofort erkennen, wie groſs diese Abweichung sein wird.
Wir nennen dem entsprechend die Strecke ZJ die
unausgeglichene Energie Dieselbe erscheint aber nur in der gedachten
Gröſse, wenn die Anzahl n der vom Linienzug in Fig.
5 eingeschlossenen und schraffirten Dreiecke eine ungerade ist. Je nach
der Gröſse des Winkels ψ kann n ungerade oder gerade
ausfallen. Der letztere Fall ist der Fig. 6 zu
Grunde gelegt. Legen wir durch die Eckpunkte des gebrochenen Linienzuges Verticalen,
so finden wir, wenn von N anfangend der den
Energieverlust 2 E1
berücksichtigende Linienzug gebildet wird, daſs wir dann auf dem Wege NP2V2X2ZTQ nach Z1 kommen, wobei JZ1= 2 E1 ist. In diesem Falle
ist also die Strecke Z1J die unausgeglichene Energie.
Beide Fälle unterscheiden sich also nur dadurch, daſs wenn n gerade der Abstand ZJ noch durch das Maſs 2
E1, zu verkleinern
ist.
Nun ist auch ersichtlich, wie sich die Verhältnisse gestalten, wenn die Zickzacklinie nicht
genau im Scheitelpunkt endet, welcher Fall in Wirklichkeit oft eintreten wird. In
Fig. 7 ist derselbe dargestellt. Wir haben dann wieder durch die
Eckpunkte der Zickzacklinie NV1Y1 (wobei jetzt Y1, nicht im Scheitelpunkt der Hyperbel liegt)
Verticalen zu ziehen und im Abstande 2 E1 unter N beginnend den
gebrochenen Linienzug P2V2X2ZZ1 zu bilden.
Augenscheinlich ist nun die Strecke Z1J1 die unausgeglichene Energie; Fig. 8
stellt den letzteren der beiden allgemeinen Fälle dar, indem der letzte Punkt Y1 links von der
Parabelachse zu liegen kommt. Der gebrochene Linienzug NP2V2X2TQZ1 endet auf der letzten durch Y1 gelegten Verticalen
und die Strecke Z1J1 gibt die
unausgeglichene Energie. Dieselbe kann, wie aus den Figuren hervorgeht, positiv oder
negativ ausfallen.
Im Folgenden sollen nun die Gröſsen, welche wir bis dahin in den Figuren 4
bis 8 durch Construction gefunden haben, rechnerisch bestimmt werden, wobei
sich noch interessante Beziehungen für die Verminderung der Flächen der lebendigen
Kräfte ergeben werden.
Wir legen in Fig. 9 durch
den Anfangspunkt F der Energieparabel ein
rechtwinkliges Coordinatensystem, dessen Y-Achse
parallel der Parabelachse geht, und zeichnen unter dem Winkel ψ in die Parabel die Zickzacklinie FABCD ein, wobei wir annehmen, daſs dieselbe im
Scheitelpunkt D der Parabel endige. Die Abstände der
Eckpunkte FABC von der Parabelachse bezeichnen wir der
Reihe nach mit b1 bis
b4. Gleichzeitig
verzeichnen wir unter der X-Achse das der ersten
Energieparabel entsprechende Dreieck der lebendigen Kräfte, dessen Hypotenuse als
Verstellungsgerade des Schützen unter dem Winkel φ
gegen die Horizontale geneigt ist.
Es ist nun der Inhalt des schraffirten Trapezes auf ein zweites durch A gelegtes Coordinationssystem bezogen:
\int\limits_0^sp\;ds=p_1s-s\,\frac{s\,tg\,\varphi}{2},
oder
\int\limits_0^sp\;ds=b_1s\,tg\,\varphi-\frac{s^2}{2}\,tg\,\varphi.
. . . (18)
Nach Gleichung (7) ist aber E=\frac{1}{l}\int
p\;ds, also
E=\frac{s}{l}\,tg\,\varphi\left(b_1-\frac{s}{2}\right). . .
. . . . . . . (19)
Wir messen jetzt E und T vorübergehend von der durch F gehenden horizontalen Ordinatenachse. Andererseits folgt nach Fig.
8:
T=s\,tg\,\psi . . . . . . . . . . . . . . . .
. (20)
Wenn s=b_1, so folgt nach Gleichung
(19):
J=E_{max}=\frac{{b_1}^2\,tg\,\varphi}{2\,l}. .
. . . . . . . . (21)
Es erfolgt Auslösung in der Kupplung, also Stillstellung des Schützen, wenn
T=E wird, also wenn, unter Bezeichnung der horizontalen
Projection von FA mit s0, nach Gleichung (20) und (19),
s_0\,tg\,\psi=\frac{s_0}{l}\,tg\,\varphi\left(b_1-\frac{s_0}{2}\right)
ist. Hieraus folgt:
b_1=\frac{s_0}{2}+\frac{l\,tg\,\psi}{tg\,\varphi}. . . . . .
. . . . . . . . (22)
Aus der Figur 8
folgt nun b_2=s_0-b_1 oder auch
b_2-b_1=s_0-2\,b_1. Führen wir auf der rechten Seite für b1 den Werth aus
Gleichung (22) ein, so folgt:
b_2-b_1=s_0-s_0-\frac{2\,l\,tg\,\psi}{\tg\,\varphi}=\frac{-2\,l\,tg\,\psi}{tg\,\varphi}.
. . (23)
Die Differenz zweier auf einander
folgender Abstände der Eckpunkte der Zickzacklinie von der Parabelachse ist
somit constant.
Setzen wir:
\frac{2\,l\,tg\,\psi}{tg\,\varphi}=a, . . . .
. . . . . . . . . . . . . . (24)
so folgt b_2=b_1-a. Ebenso folgt nun, wie
leicht einzusehen, b_3=b_2-a=b_1-2\,a und
b_4=b_3-a=b_1-3\,a, also allgemein:
b_n=b_1-(n-1)\,a . . . . . . . . . . . . .
(25)
Wir können nun weiter bilden b_n-b_{n+1}=a. Setzen wir hier den
Werth von bn aus
Gleichung (25) ein, so folgt b_1-(n-1)\,a-b_{n+1}=a. Nun ist
aber, da wir die Zahl der schraffirten Dreiecke ausdrücklich = n setzten, b_{n+1}=0, somit
folgt:
b_1-(n-1)\,a=a und b_1=n\,a
. . . . (25a)
Die Abstände b sind gleichzeitig auch die Basen der
Beschleunigungsdreiecke (Dreiecke der lebendigen Kräfte); da nun
p=b\,tg\,\varphi ist, so folgt auch nach Gleichung (25):
p_n=b_n\,tg\,\varphi=[b_1-(n-1)\,a]\,tg\,\varphi . . .
(26)
oder wenn wir b_1\,tg\,\varphi=p_1 und
a\,tg\,\varphi=e einer constanten Gröſse setzen:
p_n=p_1-(n-1)\,e . . . . . . . . . . . . . .
(27)
Aus der Gleichung a=\frac{2\,l\,tg\,\psi}{tg\,\varphi} folgt:
a\,tg\,\varphi=2\,l\,tg\,\psi=e . . . . . . .
. . . . . . . (28)
Aus Gleichung (25a) ergibt sich
n=\frac{b_1}{a}=\frac{b_1\,tg\,\varphi}{2\,l\,tg\,\psi}. Nun
ist aber b_1=\frac{p_1}{tg\,\varphi}, daher folgt:
n=\frac{p_1}{2\,l\,tg\,\psi}. . . . . . . . .
. . . . . . . . . . . . (28a)
Beachten wir, daſs, wie aus Fig. 4
unmittelbar folgt, die Zahl n auch die Anzahl der
Maxima und Minima der Energiecurve, also auch der Geschwindigkeitscurve ist, so
erkennen wir in dem Werthe n die Anzahl Schwankungen, die im
Gange des hydraulischen Motors vom Beginn der Gleichgewichtsstörung bis zur Wiedergewinnung des
neuen Beharrungszustandes vorkommen.
Aus Gleichung (25) und (27) folgt somit folgender Satz: Die
Abstände b in dem gebrochenen Linienzug der Federdruckgeraden, sowie die
beschleunigenden verzögernden Kräfte nehmen hinsichtlich ihrer absoluten Gröſse
nach einer arithmetischen Progression ab.
Die charakteristische Strecke ZJ bezieh. Z1J in Fig. 5 und
6 nannten wir die unausgeglichene Energie.
Bezeichnen wir dieselbe mit Ez, so ist nach Gleichung (5):
E_z=\frac{1}{l}\left(\frac{{v_z}^2-{v_0}^2}{2}\right);
dividiren wir diese Gleichung beiderseits mit v02, so ist:
\frac{E_z\,l}{{v_0}^2}=\frac{{v_z}^2-{v_0}^2}{2\,{v_0}^2}. .
. . . . . . (29).
Man bezeichnet bekanntlich den Quotienten
\frac{{v_z}^2-{v_0}^2}{2\,{v_0}^2} mit i, wobei man i den Ungleichförmigkeitsgrad nennt. Hier haben wir wegen der
Bedeutung von Ez die
Gröſse v0 als die dem
anfänglichen Beharrungszustande entsprechende Geschwindigkeit und die Gröſse vz als die nach der
Gleichgewichtsstörung wiedergewonnene neue Normalgeschwindigkeit zu betrachten.
Danach ist i der Ungleichförmigkeitsgrad, der nach
erfolgter Regulirung noch im Motor zurückbleibt. Offenbar muſs i den kleinstmöglichen Werth erhalten. Es folgt aus
Gleichung (29): \frac{E_z\,l}{{v_0}^2}=i. Setzen wir
\frac{{v_0}^2}{l}=A einer constanten Gröſse, so folgt:
i=\frac{E_z}{A} . . . . . . . . . . . . . . .
(30)
Daraus ergibt sich, daſs i um so
kleiner wird, je kleiner E ausfällt.
Nicht allein die Dreiecke der lebendigen Kräfte befolgen hinsichtlich ihrer
allmäligen Verminderung eine gewisse Gesetzmäſsigkeit, sondern auch die Rechtecke
derselben. Bezüglich dieser folgt auf Grund der Gleichung (10) der Satz: der Inhalt der Rechtecke der lebendigen Kräfte ist
constant. Da nun die Höhen derselben gleich den in arithmetischer
Progression abnehmenden Beschleunigungsordinaten sind, so ist damit auch das Gesetz
bestimmt, wonach sich die Basen x der Rechtecke
allmälig vergröſsern.
Es folgt durch Verbindung von Gleichung (10) mit (27):
x_n=\frac{J}{p_n}=\frac{J}{p_1-(n-1)\,e}=\frac{\frac{G}{Ph}\,\frac{U^2}{u^2}\,R^2\,(E_0+E_2)}{p_1-(n-1)\,2\,l\,tg\,\psi}.
. . . . (31)
Es bleibt nun noch ein Specialfall zu behandeln, welcher bei der Regulirung oft
eintritt.
(Schluſs folgt.)
Tafeln