| Titel: | Die Luftmaschine von D. W. van Rennes. |
| Autor: | A. Slaby |
| Fundstelle: | Band 231, Jahrgang 1879, S. 119 |
| Download: | XML |
Die Luftmaschine von D. W. van Rennes.
Mit Abbildungen auf Tafel 12.
Slaby, über Rennes' Luftmaschine.
Zu denjenigen Luftmaschinen, welche mit einem und demselben Luftgewicht arbeiten, und
die man in Folge dessen „geschlossene Luftmaschinen“ nennt, ist im Laufe des
letzten Jahres eine neue Construction holländischen Ursprunges hinzugekommen. Die
Luftmaschine von D. W. van Rennes, in Deutschland
vertreten durch die Fabrik von Fredenhagen in
Offenbach, nahm auf der Fachausstellung der Kraft- und Arbeitsmaschinen für das
Kleingewerbe in Erfurt im August v. J. die Concurrenz mit den bereits bewährten und
in Deutschland verbreiteten Constructionen von Lehmann
und von Stenberg (*1878 228 391) auf. In Erfurt hatte
der Verfasser Gelegenheit, die nachfolgenden Studien und Messungen vorzunehmen.
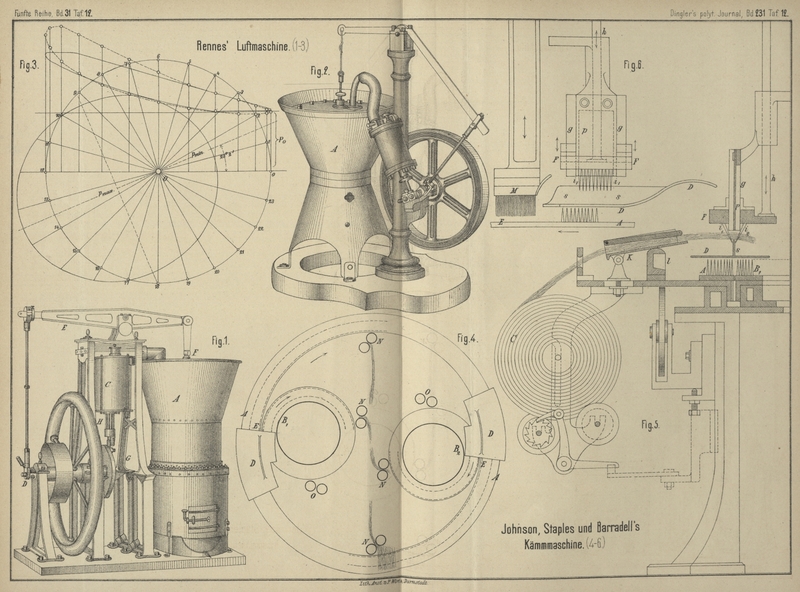
Fig.
1 und 2 Taf. 12
zeigen zwei verschiedene Anordnungen des Rennes'schen
Motors. Der Erfinder hat das seit mehr als 10 Jahren verlassene Zweicylindersystem
von Stirling und Laubereau
(1876 219 196) wieder aufgenommen. Wie bei diesen ist
auch bei ihm der Arbeitscylinder gesondert vom Verdrängercylinder angeordnet, mit
der einzigen Abänderung, daſs der Arbeitscylinder oscillirend ausgeführt ist. Zwar
ist bei der neueren Construction Fig. 1 die
ganz untaugliche Verbindung des Arbeitscylinders mit dem Verdrängercylinder durch
ein biegsames Rohr (Fig. 2)
durch die bessere mit Hilfe eines hohlen Zapfens ersetzt worden; doch hat auch diese
Anordnung alle Nachtheile des Zweicylindersystemes aufzuweisen, wozu in erster Linie
die Vergröſserung der schädlichen Räume zu rechnen ist, die man grade in
geschlossenen Luftmaschinen ängstlich zu vermeiden hat. In klarer Erkenntniſs dieses
Uebelstandes hatte Lehmann seinerzeit das
Zweicylindersystem verlassen und durch seine eincylindrige Construction das
berechtigte Miſstrauen, das gegen alle Luftmaschinen Platz gegriffen hatte, in
Deutschland wenigstens siegreich bekämpft.
Es scheint kaum nöthig, das auch der Rennes'schen
Maschine zu Grunde liegende Princip der geschlossenen Luftmaschinen noch einmal zu
erläutern. Ein bestimmtes, in der Maschine verbleibendes Luftgewicht wird
abwechselnd erhitzt und abgekühlt; die dadurch hervorgerufene Variation in der
Spannung wird in einem mit Kolben versehenen Arbeitscylinder ausgenutzt, indem durch
den Kolben die Compression erfolgt, während die gröſsere Menge der eingeschlossenen
Luft kalt, die Expansion dagegen vollzogen wird, während die gröſsere Menge der
eingeschlossenen Luft warm ist. Der Ueberschuſs der Expansionsarbeit der heiſsen
Luft über die Compressionsarbeit der kalten Luft ist die Production der Maschine an
nutzbarer Arbeit, welche in geeigneter Weise einem Schwungrade mitgetheilt werden kann. Die abwechselnde
Erhitzung und Kühlung der eingeschlossenen Luft wird bei der Rennes'schen Maschine in einem besonderen cylindrischen Gefäſs A durch den sogen. Verdränger bewirkt. Der Verdränger
ist ein aus Blech luftdicht genieteter, allseitig verschlossener Hohlcylinder,
dessen Durchmesser etwas kleiner ist als der Durchmesser des Cylinders A, so daſs zwischen beiden ein ringförmiger Raum
bleibt, durch den die Luft vom oberen Theil des Cylinders in den unteren gelangen
kann. Die Wandungen des unteren Theiles des Cylinders A
sind in einem Ofen dem Feuer ausgesetzt und werden während des Betriebes
rothglühend. Recht hübsch und einfach ist bei Rennes
die Kühlung des oberen Theiles des Cylinders A durch
einen oben offenen Wassermantel. Das Wasser kann ohne Schaden zum Sieden gebracht
werden, wobei nur nach Maſsgabe der Verdampfung ein Ersatz bewirkt werden muſs; im
regelmäſsigen Betriebe steigt jedoch die Temperatur nur selten auf Siedhitze. Die
Hubbewegung des Verdrängers erfolgt durch eine Kurbel D
(Fig. 1) mittels des Balancier E und der
Kolbenstange F, welche in einer gut gedichteten
Stopfbüchse durch den Deckel des Verdrängercylinders geführt ist. Schlieſslich ist
noch die Arbeitskurbel G zu erwähnen, welche durch die
Kolbenstange H mit dem Kolben des unten offenen
oscillirenden Arbeitscylinders C verbunden und gegen
die Verdrängerkurbel D um 95° versetzt ist.
Die Anordnung Fig. 2 mit
der biegsamen Rohr Verbindung wird von Rennes aus
leicht begreiflichen Gründen für gröſsere Maschinen bis zu 1 und 2e nicht mehr verwendet, wohl aber noch für die
kleinen Modelle von 2 bis 3mk, von denen ein durch
Gas geheiztes Exemplar auf der Erfurter Ausstellung für den Betrieb einer
Nähmaschine aufgestellt war. Diese kleine Maschine arbeitete auſserordentlich sicher
und ruhig und blieb sich vollständig selbst überlassen. Für kleinste Arbeitsleistungen, bei welchen der Brennmaterial verbrauch keine
nennenswerthe Rolle spielt, scheint hiernach die Zukunft der Maschine gesichert; nur
müſste der immerhin noch hohe Preis (180 M.) erheblich vermindert werden können.
Es soll im Folgenden eine gedrängte Berechnung der Arbeitsleistung der Maschine
gegeben werden, aus welcher dann an der Hand der Versuchsresultate sich einige
interessante Folgerungen ergeben. Die Dimensionen der in Erfurt ausgestellten,
nominell 1e-Maschine waren die folgenden:
m
Durchmesser des Arbeitscylinders
0,261
Kolbenhub
0,297
Durchmesser des Verdrängercylinders
0,500
Durchmesser des Verdrängerkolbens
0,493
Hub des Verdrängerkolbens
0,070
Länge des Verdrängercylinders
1,050
Länge des Verdrängerkolbens
0,975
m
Minimalentfernung des Verdrängers vom Heizbodensowie vom
Deckel
0,0025
Die Voreilung der Verdrängerkurbel gegen
dieArbeitskurbel
95°
Rauminhalt des Verbindungsrohres zwischen
Ver-drängercylinder und Arbeitscylinder
0cbm,001176.
Zur Vereinfachung der Rechnung sollen zunächst folgende
Annahmen gemacht werden: 1) In den heiſsen und kalten Räumen der Maschine herrschen
constante Temperaturen. 2) Der Uebergang der Temperaturen erfolgt nicht allmälig,
sondern plötzlich. 3) Der Rauminhalt der ringförmigen Verdrängerspalte wird zur
Hälfte zum heiſsen und zur Hälfte zum kalten Raum hinzugerechnet. – Die absoluten
Temperaturen des heiſsen und kalten Raumes seien bezieh. T1 und T2.
Die Farbe des Heiztopfes war während der Dauer des Versuches eine normale
Dunkelrothgluth, einer Temperatur von etwa 500° entsprechend; nimmt man die
Temperatur des kalten Raumes auf 110 bis 115° an, so ergibt sich hieraus das
Verhältniſs der absoluten Temperaturen:
\frac{T_1}{T_2}=\frac{273+500}{273+112}\sim
2,00 . . . . . (1)Es mag auffallend erscheinen, daſs diese wichtige Constante, welche in der
Berechnung der Leistung eine bedeutende Rolle spielt, an dieser Stelle durch
immerhin unsichere Schätzung bestimmt wird. In der That ist sie von mir nicht durch Schätzung bestimmt worden, sondern auf einem mühseligen und
zeitraubenden Wege, dessen theoretische Begründung und Herleitung in den Verhandlungen des Vereines zur Beförderung des
Gewerbfleiſses, 1878 S. 375 veröffentlicht ist. Nur so viel, daſs
die Ermittlung aus der Form der Diagramme im Zusammenhang mit der Steuerung
erfolgt, und daſs ich unter dem Werth \frac{T_1}{T_2}
eine Constante der Maschine verstehe, welche zwar im Wesentlichen ein Mittelwerth der auftretenden
Temperaturverhältnisse ist, im Uebrigen aber auch von sonstigen
gesetzmäſsigen und zufälligen Einflüssen, als Verhältniſs der Heiz- und
Kühlflächen, Geschwindigkeit des Luftstromes, Länge des Verdrängers, Weite
der Spalte u. dgl. abhängt.
Reducirt man sämmtliche Maſse auf den Querschnitt des Arbeitskolbens
(F=0^{qm},053502), so ergeben sich folgende Werthe:
m
Halber Hub des Arbeitskolbens
r =
0,149
Halber Hub des Verdrängers
R =
0,132
Länge des constanten kalten Raumes
ek =
0,031
Länge des constanten heiſsen Raumes
eh =
0,009
Länge des Verdrängers
L =
1,880
Querschnittfläche des Verdrängers
f =
0qm,050671.
Zählt man die Kurbelwinkel von dem äuſseren Todtpunkt aus, so berechnet sich für
einen beliebigen Kurbelwinkel φ der in der Maschine
vorhandene heiſse Raum (auf die Kolbenfläche reducirt) in einfacher Weise:
h=0,190+0,132\;cos\,(\varphi+95^{\circ}). . .
. . (2)
Für den kalten Raum findet man bei demselben Kurbelwinkel
k=0,287+0,149\;cos\,\varphi-0,132\;cos\,(\varphi+95^{\circ}),
oder unter Einführung eines Hilfswinkels ε:
k=0,287+0,207\;cos\,(\varphi-\varepsilon), . .
. . . (3)
worin \varepsilon=39^{\circ}26'20''. Für
\varphi=0 mögen die entsprechenden Werthe mit h0 und k0 bezeichnet werden.
Es folgt:
k_0=0,447 \;\ldots\; h_0=0,179 . . . (4) und
(5)
Die Spannung, welche in beiden Räumen der Maschine wegen der freien Verbindung
derselben gleich groſs ist, betrage pk auf 1qm: Es bezeichne ferner gh das Luftgewicht des heiſsen Raumes, gk dasjenige des kalten
und R die Constante der Luft = 29,27. Dann ist nach dem
Mariotte-Gay-Lussac'schen Gesetz:
g_h=F\,\frac{hp}{RT_1} und
g_k=\F\,\frac{kp}{RT_2}.
Das gesammte eingeschlossene Luftgewicht sei G, dann ist:
G=g_h+g_k=\left(\frac{k}{T_2}+\frac{h}{T_1}\right)\,\frac{Fp}{R}.
Bezeichnet man die Spannung in der Kurbelstellung
\varphi=0 mit p0, so ist auch:
G=\left(\frac{k_0}{T_2}+\frac{h_0}{T_1}\right)\,\frac{Fp_0}{R}.
Das eingeschlossene Luftgewicht ist in beiden Fällen dasselbe;
es folgt hieraus die Fundamentalgleichung:
\left(\frac{k}{T_2}+\frac{h}{T_1}\right)p=\left(\frac{k_0}{T_2}+\frac{h_0}{T_1}\right)p_0=\mbox{Const.}
. . . (6)
Setzt man in diese Gleichung die oben berechneten Werthe, so
erhält man:
\frac{p}{p_0}=\frac{3,193}{2,273+cos\,(\varphi-\beta)}, . .
. . . . (7)
worin β ein Hilfswinkel und =
23°2' ist.
Die Maximaluntersuchung liefert für \varphi=\beta das Minimum und
für \varphi=180+\beta das Maximum; es wird
p_{min}=0,975\,p_0 und
p_{max}=2,508\,p_0.
Soll die Maschine mit Luft von atmosphärischer Spannung arbeiten, so muſs
p_0=10000 sein, mithin wird:
p_{min}=9750^k\;\mbox{auf}\;1^{qm}. . . . . .
. . . (8)
p_{max}=25080^k\;\mbox{auf}\;1^{qm}. . . . . .
. . (9)
Bezeichnet man das Gesammtvolum der eingeschlossenen Luft bei einem beliebigen
Kurbelwinkel und reducirt auf die Kolbenfläche mit v,
so ist die bei einer Umdrehung geleistete Arbeit:
L=F\int_{\varphi=0}^{\varphi=2\,\pi}\,p\,dv.
Es ist aber v=F\,(h+k)=F\,(0,477+0,149\,cos\,\varphi).
Setzt man für p und v die erhaltenen Werthe ein, so gibt die Lösung des
bestimmten Integrals die für jede Umdrehung übertragene Arbeit, oder nach Division durch
Kolbenhub und Kolbenfläche die nutzbare Mittelspannung:
P=4658^k\;\mbox{auf}\;1^{qm} . . . . . . . . .
. . (10)
Das eingeschlossene Luftgewicht läſst sich am schnellsten in der Kurbelstellung
\varphi=0 berechnen. Es ist:
G=F\left(k_0+\frac{h_0}{\frac{T_1}{T_2}}\right)\frac{p_0}{RT_2}=0^k,025471
. . (11)
Für die Berechnung der hubweise zuzuführenden Wärmemenge soll folgende Ueberlegung
maſsgebend sein. Das gesammte eingeschlossene Luftgewicht nimmt an der Aufnahme
bezieh. Abgabe der Wärme nicht Theil. Ein gewisser Procentsatz des Luftgewichtes,
derjenige, welcher die sog. schädlichen Räume der Maschine füllt, behält während der
ganzen Dauer des Arbeitsprocesses seine Temperatur:, der eine Theil dieses
Procentsatzes befindet sich im heiſsen Raum der Maschine, der andere im kalten. Die
Summe beider mag als ruhendes Luftgewicht bezeichnet werden, während der übrig
bleibende Theil des eingeschlossenen Luftgewichtes zweckmäſsig das wirkende
Luftgewicht genannt werden kann. Beide sollen für die mittlere, in der Maschine
herrschende Spannung berechnet werden. Bezeichnet man die letztere mit pm, so ist das gesammte
ruhende Luftgewicht:
G_r=F\left(k_{min}+\frac{h_{min}}{\frac{T_1}{T_2}}\right)\frac{p_m}{RT_2}.
Durch eine Minimaluntersuchung der Formeln (2) und (3) folgt:
h_{min}=0,058 und k_{min}=0,080; ferner
nach (10): p_m=14658. Es ergibt sich nach Einsetzung dieser
Gröſsen:
G_r=0^k,007586 . . . . . . . . . . . . . . .
(12)
Nach Abzug des ruhenden Luftgewichtes vom gesammten eingeschlossenen erhält man das
wirkende Luftgewicht:
G_w=G-G_r=0^k,017885. . . . . . . . (13)
Bei jedem Hub der Maschine ist dieses Luftgewicht von der
Temperatur T2 auf die
Temperatur T1 zu
bringen. Die zuzuführende Wärmemenge findet sich nach der bekannten Formel:
Q_1=G_wc_p\,(T_1-T_2), worin cp die specifische Wärme der Luft bei
constantem Druck = 0,23751 bedeutet. Es ist:
Q_1=1^c,6481 . . . . . . . . . . . . . . . . .
(14)
Bezeichnet man die für jeden Hub abzuführende Wärmemenge mit Q2, so ist Q1– Q2 die während des Arbeitsprocesses in nutzbare
Arbeit umgesetzte Wärme. Letztere ist aber aus der berechneten nutzbaren
Mittelspannung P zu finden:
Q_1-Q_2=AP\,2\,rF, wenn A das
mechanische Wärmeäquivalent = 1/424. Es wird:
Q_1-Q_2=0^c,17515 . . . . . . . . . . . . .
(15)
Durch Subtraction von Q1 und Q1 – Q2 erhält man schlieſslich die hubweise abzuführende
und vom Kühlwasser aufzunehmende Wärmemenge:
Q_2=1^c,47295 . . . . . . . . . . . . . . . .
. (16)
Aus den berechneten Wärmewerthen läſst sich ein Schluſs in Bezug auf die Güte des
Arbeitsprocesses ziehen. Von Q1 Wärmeeinheiten, welche für jeden Hub zugeführt
werden, setzt die Maschine Q1 – Q2
Wärmeeinheiten in nutzbare Arbeit um. Der Quotient
\frac{Q_1-Q_2}{Q_1} spielt in der Theorie der Luftmaschinen
eine ähnliche Rolle wie das Güteverhältniſs in der Theorie der Dampfmaschinen. Es
soll deshalb für den vorliegenden Zweck derselbe Name beibehalten werden. Es findet
sich das Güteverhältniſs für die Rennes'sche Maschine
hiernach:
\eta=\frac{Q_1-Q_2}{Q_1}=0,10.
Bezieht man dieses Güteverhältniſs auf seinen Maximalwerth, d.h. auf das Güteverhältniſs des zwischen denselben
Grenztemperaturen T1 und T2 arbeitenden Carnot'schen Kreisprocesses, so erhält man den
Zeuner'schen Wirkungsgrad. Der Maximalwerth des Güteverhältnisses wird in
diesem Fall: \frac{T_1-T_2}{T_1}=0,50, der Zeuner'sche
Wirkungsgrad mithin = 0,20.
Das Resultat ist allerdings ungünstig genug: Von derjenigen Wärmemenge, welche der Luft wirklich
zugeführt wird, läſst sich nur der zehnte Theil in Arbeit umsetzen. Rechnet man
den Nutzeffect der Feuerung zu 0,50, so setzt die Rennes'sche Luftmaschine von
der in den zugeführten Kohlen vorhandenen Wärmemenge 5 Proc. und unter
Berücksichtigung eines WirkungsgradesGebremste Arbeit dividirt durch indicirte Arbeit. Vergleichsweise mag
angeführt werden, daſs man in groſsen Dampfmaschinen neuerer
Construction vom Wärmewerth der Kohlen bis zu 10 Proc. in nutzbare
Arbeit umsetzen kann. von 0,50, etwa 2,5 Proc. in nutzbare
Arbeit um.
Zum Schluſs mag noch die Kohlenberechnung folgen. Für jeden Hub sind Q1 Wärmeeinheiten
zuzuführen. Nimmt man an, daſs die Maschine, wie von der Fabrik behauptet wird, 130
Touren in der Minute machen kann, so stellt sich die Leistung bei einem Wirkungsgrad
von 0,50 auf: L=\frac{0,053502\times 4658\times 130\times 2\times
0,149}{60\times 75\times 2}\sim 1^e. Rechnet man den Heizwerth der
Kohlen zu 6000°, so ergibt sich der Kohlen verbrauch für Stunde und Pferdestärke bei
0,50 Nutzeffect der Heizung: K=\frac{Q_1\times 130\times 60}{6000\times
0,5}=4^k,28.
Gemeinsam mit Herrn Docent Brauer wurde vom Verfasser
auf der Erfurter Ausstellung das nachfolgende Protokoll über eine mit der Rennes'schen Maschine vorgenommene Kraftmessung
aufgenommen:
Bericht über die mit einer Rennes'schen Heiſsluftmaschine von nominell 1e auf der Ausstellung von Kraft- und Arbeitsmaschinen für das Kleingewerbe
in Erfurt durch das Preisgericht vorgenommenen Brems- und Indicatorversuche.
Die Versuche bezweckten die Feststellung des
Brennmaterialverbrauches für Pferdestärke und 10stündigen Arbeitstag. Letztere
Bezugseinheit wurde gewählt, um die täglich erforderliche Kohlenmenge für das
Anheizen in richtiger Weise berücksichtigen zu können. Die Versuche zerfielen in 4
Perioden, von denen die erste für das Anheizen, die zweite und dritte für den
Arbeitsgang und die vierte für den Auslauf bestimmt war. Die Mittelwerthe aus den
einzelnen Betriebsresultaten sind in folgender Tabelle zusammengestellt:
Durchmesser des Arbeitscylinders
261mm
Hub des Arbeitskolbens
297mm
Nummer der Periode
I
II
III
IV
Datum des Versuches
6. Aug. 1878
6. Aug. 1878
6. Aug. 1878
6. Aug. 1878
Zeit
11 U. 50–1 U. 25
1 U. 25–1 U. 35
1 U. 35–5 U. 24
5 U. 24–6 U. 20
1
Dauer der Periode
1 St. 35 M.
10 Min.
3 St. 49 M.
56 Min.
2
Mittlere Tourenzahl
–
57,75
99,16
99,16 bis 0
3
Reducirte Belastung derBremse
–
3k,61
3kg,11
3,11 bis 0
4
Hebellänge der Bremse
–
1m,187
1,m187
1m,187
5
Nutzbarer Mitteldruck
–
0k,328
0k,282
6
Anzahl der berechnetenDiagramme
–
2
8
–
7
Gebremste Arbeitsstärke
–
0e,345
0e,594
0,594 bis 0
8
Indicirte Arbeitsstärke
–
0e,69
1e,02
1,02 bis 0
9
Wirkungsgrad
–
0,50
0,58
–
10
Brennmaterialverbrauch:
a) Steinkohle
–
6k
b) Kokes
13k,7
11k
c) Kiefernholz
1k
–
11
Brennmaterialverbrauchfür Stunde u. Pferdest.für die II. u. III.
Periode
7k,3
Gemisch
12
Brennmaterialverbrauchfür Pferdestärke und10 stünd.
Arbeitstag
97k,6
Gemisch
Bemerkung. Bei Berechnung der letzten Zahl ist 1k Holz = ⅔k
Kokes gesetzt, demnach die zum Anheizen erforderliche Brennmaterialmenge = 14k,4 Kokes. Da 4 Stunden Arbeit 17k Brennmaterial brauchten, so wären in 10 Stunden
42,5 erforderlich, also eingeschl. Anheizen 56k,9
für 0e,583 im Mittel, hiernach für Tag und Pferd =
56,9 : 0,583 = 97k,6 Gemisch.
E.
Brauer. Dr. A. Slaby.
Zunächst ist aus dem Protokoll die Thatsache zu entnehmen, daſs die Leistung der
Maschine durchweg weit unter der von der Fabrik angegebenen und im Obigen durch
genaue Rechnung controlirten Höhe geblieben ist. Berücksichtigt man für den
Vergleich nur die dritte Periode (von 3 Stunden 49 Minuten Länge), während welcher
die Maschine eine ziemlich constante Leistung aufzuweisen hatte, so stellen sich die
Differenzen folgendermaſsen:
Touren-zahl
NutzbarerMittel-druck
IndicirteLeistung
Nutz-leistung
Brennmaterial ver-brauch für Stundeund
Pferd
Angegeben oderberechnet
130
k auf 1qc0,4658
e2
e1
k4,28
Gemessen
99
0,282
1,02
0,594
7,3
Die Maschine arbeitete während der ganzen Dauer des Versuches geräuschlos, schien
äuſserlich in gutem Zustande und wurde von einem erfahrenen und intelligenten Heizer
bedient.
Es drängt sich nun die Frage auf, worin der Grund für diese anscheinend ganz
unverhältniſsmäſsige Minderleistung lag? Aus den Diagrammen, welche zahlreich
aufgenommen wurden und die von groſser Gleichmäſsigkeit blieben, war eine Erklärung
ohne weiteres nicht zu entnehmen. Klar wurde mir erst die Sache, als ich das
theoretische Arbeitsdiagramm construirte und mit den aufgenommenen
Indicatordiagrammen verglich.
Das Diagramm jeder geschlossenen Luftmaschine läſst sich nach folgendem Verfahren
ziemlich schnell construiren. Die Gleichung:
\frac{p}{p_0}=\frac{3,193}{2,273+cos\,(\varphi-\beta)}
kann als eine Polargleichung aufgefaſst werden und stellt eine
Ellipse dar, deren Focus mit dem Pol zusammenfällt, deren Hauptachse aber einen
Winkel – β mit der Directrix des
Polarcoordinatensystemes einschlieſst. Die Hauptachsen dieser Ellipse lassen sich
berechnen; für den vorliegenden Fall ist a=1,742 und
b=1,564,
\beta=23^{\circ}2'. Schlägt man um den Focus einen Kreis mit dem
Radius der Arbeitskurbel, so erhält man die den einzelnen Kurbelstellungen
entsprechenden Spannungen als Fahrstrahlen der Polarellipse. In Fig. 3 Taf.
12 ist die Construction durchgeführt. Die punktirte Diagrammlinie ist die
construirte, die ausgezogene dagegen die an der Maschine selbst abgenommene. In den
Kurbelstellungen 0 bis 6
und 18 bis 24 stimmen
beide Diagramme fast vollständig überein; in denjenigen Kurbelstellungen jedoch, in
denen sich der Kolben in der inneren Hälfte seines Hubes befindet, die Luft also
comprimirt ist, weichen die Diagramme erheblich von einander ab. Hiernach bleibt nur
eine Erklärung übrig: Die Maschine ist während des Versuches
undicht gewesen.Meine Vermuthung wurde durch eine nachträglich mir zugegangene Mittheilung
des Hrn. Fredenhagen bestätigt, wonach sich bei
der Zerlegung der Maschine in Utrecht im Feuertopf ein kleiner Riſs gefunden
hat.
Es wäre Unrecht, wenn man hiernach auf Grund des mitgetheilten Prüfungsprotokolls ein
absprechendes Urtheil über die Rennes'sche Maschine
fällen wollte. Daſs dies in Erfurt seitens des Preisgerichtes geschehen ist, findet
seine natürliche Erklärung darin, daſs während des fast 7stündigen Versuches keine einzige Erscheinung
auftrat, aus welcher man mit Bestimmtheit auf eine Undichtigkeit der Maschine hätte
schlieſsen können. Es muſste angenommen werden, daſs die gemessene Leistung die
wirklich normale der Maschine ist.
Dr. A. Slaby.
Tafeln