| Titel: | Dynamometer ohne Feder für Werkzeugsmaschinen; von M. Kohn in Wien. |
| Autor: | M. Kohn |
| Fundstelle: | Band 231, Jahrgang 1879, S. 229 |
| Download: | XML |
Dynamometer ohne Feder für Werkzeugsmaschinen;
von M. Kohn in
Wien.
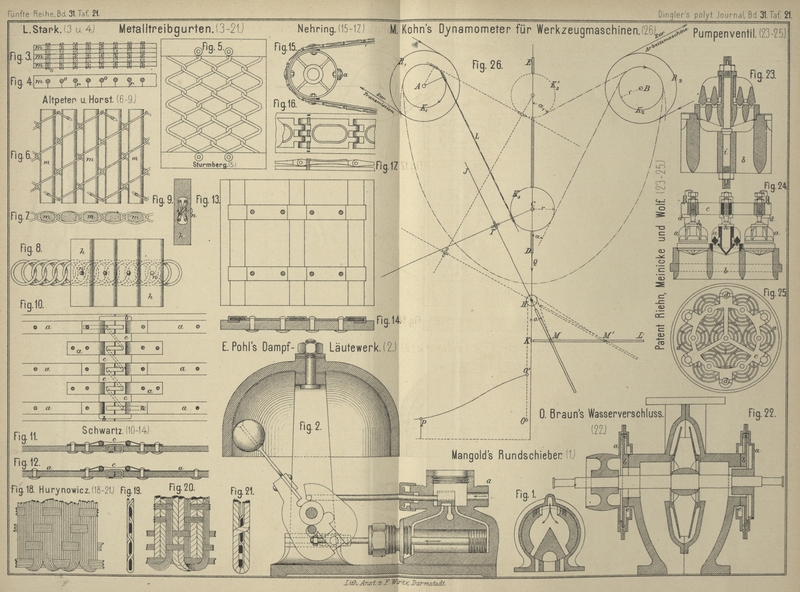
Mit einer Abbildung auf Tafel 21.
Kohn's Dynamometer für Werkzeugsmaschinen.
Das von mir erdachte Dynamometer wird zwischen der Fabrikstransmission und der zu
prüfenden Maschine derart eingeschaltet, daſs ein Riemen von der Transmission
ausgehend zuerst das Dynamometer in Thätigkeit setzt und dieses wieder die Maschine.
Das Dynamometer gibt graphisch die von der Maschine verbrauchte Arbeit, kann aber
auch wie bei Morin's Dynamometer so eingerichtet
werden, daſs es durch eine von einem Zählwerk angegebene Verhältniſszahl die Arbeit
ausdrückt. Im Nachstehenden theile ich kurz das Princip dieses Apparates mit.
Auf einer Welle des Apparates A (Fig. 26
Taf. 21) sitzt fest die Riemenscheibe R1 und das Kettenrad K1 auf der Welle B eine gleich groſse Riemenscheibe R2 und ein gleich groſses Kettenrad K2. Von der
Riemenscheibe R1 geht
ein Riemen zu einer Scheibe der Fabrikstransmission, von der Riemenscheibe R2 ein zweiter Riemen
zur Antriebsscheibe der auf ihren Arbeitsverbrauch zu untersuchenden Maschine. In
einem Schlitz ED, welcher im Halbirungspunkte der Linie
AB senkrecht auf dieselbe steht, kann sich der
Bolzen C auf und nieder bewegen. Auf diesem Bolzen
sitzt lose ein drittes Kettenrad K3 von gleichem Radius r
wie die anderen Kettenräder. Eine Gelenkkette schlingt sich auf angedeuteter Weise
um die drei Kettenräder, und durch das entsprechend gewählte Eigengewicht des
Kettenrades K3 wird der
jedesmal zwischen K1,
und K3, sowie K2 und K3 befindliche Theil
der endlosen Kette straff gespannt.
Wird nun die Riemenscheibe R, von der Transmission in
Bewegung versetzt, so macht K1 die Drehung mit; durch die endlose Kette wird auch K2, ebenso R2 und schlieſslich die
zu untersuchende Maschine bewegt. Das Kettenrad K3 wirkt dabei als eine Art von Spannrolle. Nehmen
wir vorläufig an, die Geschwindigkeit wäre während der Untersuchung immer dieselbe,
sehen ebenfalls von den Reibungswiderständen und dem Gewicht der Kette ab und denken
uns die zu untersuchende Maschine einen Widerstand überwindend. Der bei einer
gewissen Geschwindigkeit aufgebrauchten Arbeit entspricht eine Kraft P, am Umfange des Kettenrades wirkend gedacht. Diese
Kraft wird sich als Zugkraft in dem Kettentheile zwischen K3 und K2 äuſsern. Ein gleich groſser Zug tritt bei der
gewählten Anordnung im Kettentheil zwischen K1 und K3 auf. Diesen beiden Kräften P hat nun das Eigengewicht Q des Kettenrades
K3 das
Gleichgewicht zu halten, was in der Art geschieht, daſs ½Q = P cos α. Wenn sich also P ändert, wird die Lage der Rolle wechseln, weil sich a ändern muſs. Ein an K3 angebrachter Stift würde auf einem horizontal
bewegten Papier eine Curve beschreiben, deren Ordinaten eine Function der Kraft,
also nicht direct proportional der Kraft wären.
Die nun noch angedeuteten Theile des Apparates sollen nun einen Stift derart auf und
nieder bewegen, daſs der Hub direct proportional der am Umfange von K2 oder K1, wirkenden Kraft
ist. Auf A und C sind zwei
Arme lose aufgesteckt, welche im Abstande r des
Kettenrades vom Drehungspunkt eine Hülse senkrecht gegen ihre Achse besitzen. Durch
diese Hülsen geht das Stängelchen L, welches auf diese
Weise immer die Theilkreise von K1, und K3 tangirt. Der in C
aufgesteckte Arm ist über die Hülse hinaus verlängert, um eine zweite verschiebbare
Hülse T aufzunehmen; dieselbe ist mit einer zweiten
unter einem rechten Winkel stehenden Hülse zusammengegossen, in welcher die um den
fixen Punkt H drehbare Spindel J steckt. Durch diese ganze Anordnung wird nun bewirkt, daſs die Spindel
J immer parallel zum Kettenstück zwischen K1 und K3 bleibt. Die Spindel
J, über H hinaus
verlängert, hat einen Schlitz; in diesen und den Schlitz KL greift gleichzeitig der Bolzen M ein (KL senkrecht EU). Von M geht eine Schnur über das möglichst klein zu haltende
Röllchen bei H nach abwärts und trägt am Ende einen
Stift O, der so geführt ist, daſs er sich nur vertical
auf und nieder bewegen kann.
Wächst der Widerstand in der Werkzeugsmaschine, dann geht K3 nach aufwärts in die punktirt
gezeichnete Lage K3,
ebenso M nach M', der
Stift O nach O'.
Angenommen, P sei die Kraft, welcher der voll, P1 die Kraft, welcher
der punktirt gezeichnete Zustand entspricht, so hat man:
P=\frac{1/2\,Q}{cos\,\alpha} und
P_1=\frac{1/2\,Q}{cos\,\alpha_1}
Bezeichnet man HK=nQ, so ist:
HM=\frac{nQ}{cos\,\alpha} und
HM_1=\frac{nQ}{cos\,\alpha_1} oder
HM_1-HM=OO'=\lambda\,(P_1-P),
d.h. der vom Stift O
zurückgelegte Weg ist direct proportional der Kraftänderung. Wenn die Abscissenachse
entsprechend gewählt ist, so gibt die jeweilige Entfernung des Stiftes von der Achse
die Gröſse der Kraft direct in einem bestimmten Maſsstabe an.
Wenn nun durch ein von K2 bethätigtes Zählwerk ein Papierstreifen, gegen welchen O drückt, normal auf die Bewegungsrichtung des Stiftes
vorgeschoben wird, so wird die vom Stift beschriebene Diagrammfläche die von der
Maschine verbrauchte Arbeit angeben, zugleich auch zeigen, wie die Kraft sich in den
verschiedenen Arbeitsphasen geändert hat.
Tafeln