| Titel: | Bestimmung des specifischen Gewichtes pulverförmiger Körper. |
| Fundstelle: | Band 232, Jahrgang 1879, S. 417 |
| Download: | XML |
Bestimmung des specifischen Gewichtes
pulverförmiger Körper.
Mit einer Abbildung auf Tafel 38.
Rüdorff's Dichte-Bestimmung für pulverförmige Körper.
Der zu diesem Zweck von F. Rüdorff in den Berichten der deutschen chemischen Gesellschaft, 1879
S. 249 mitgetheilte Apparat miſst das durch den zu untersuchenden Körper verdrängte
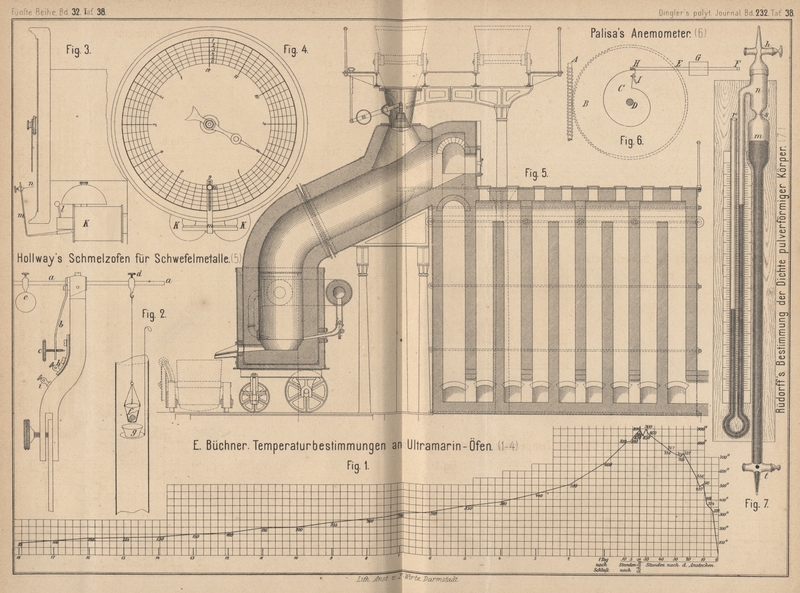
Volum Luft. Das Glasgefäſs n (Fig. 7 Taf.
38) von etwa 25cc Inhalt ist durch einen engen,
die Marke s tragenden Hals mit dem Gefäſse m von etwa 40cc
Inhalt verbunden, welches wieder in ein etwa 65mm
langes und 10mm dickes Glasrohr mit dem Hahn t ausläuft. Das Gefäſs n
trägt seitlich das Manometer r und oben eine
aufgeschliffene Kappe mit dem Glashahn h.
Zur Anstellung eines Versuches wird das Manometer r zur
Hälfte, das Gefäſs m nebst Rohr aber bis in das Gefäſs
n mit Quecksilber gefüllt. Durch Oeffnen des Hahnes
t wird nun das Quecksilber bis zur Marke s abgelassen, ein passendes Glasrohr in das Gefäſs n gebracht, die Kappe bei geöffnetem Hahn h fest aufgesetzt und dieser dann geschlossen. Nun wird
durch Oeffnen des Hahnes t so lange Quecksilber
abgelassen, dessen Volum durch Wägung bestimmt wird, bis das Manometer eine
Druckverminderung von etwa 0at,5 zeigt. Dann wird
ein zweiter Versuch in derselben Weise gemacht, nur wird das Glasrohr in n mit der zu untersuchenden Substanz, deren Gewicht
vorher ermittelt ist, gefüllt. Hierbei ist darauf zu achten, daſs der Stand des
Quecksilbers im Manometer genau derselbe ist wie im ersten Versuch, so daſs also der
Druck im Innern des Apparates in beiden Versuchen gleich ist. Aus zwei solchen
zusammengehörigen Versuchen läſst sich das Volum der verdrängten Luft berechnen.
Bezeichnet man den Abstand der Quecksilberoberflächen im Manometer
mit m, den von einem Barometer abgelesenen Luftdruck
mit b, so ist b – m = d der Druck, unter
welchem sich die Luft im Apparat befindet. Ferner sei q
das Volum des im ersten, q' das Volum des im zweiten
Versuch abgelassenen Quecksilbers. Mit v und v' sei das gesammte Volum der Luft im ersten und
zweiten Versuch bezeichnet. Das Volum des Röhrenabschnittes, in welchem das
Quecksilber in dem einen Manometerschenkel steigt, sei x, dann verhält sich v:(v+q-x)=(b-m):b und
v':(v'+q'-x)=(b-m):b.
Aus diesen beiden Gleichungen folgt, wenn man schlieſslich
(b-m)=d setzt: v-v'=\frac{(q-q')\,d}{m};\
v-v' ist aber das Volum des zu untersuchenden Körpers. Es läſst sich
dieses also aus den Werthen q, q', m und b berechnen.
Tafeln