| Titel: | Georg Fuller's Spiral-Rechenschieber. |
| Fundstelle: | Band 233, Jahrgang 1879, S. 208 |
| Download: | XML |
Georg Fuller's Spiral-Rechenschieber.
Mit einer Abbildung auf Tafel 18.
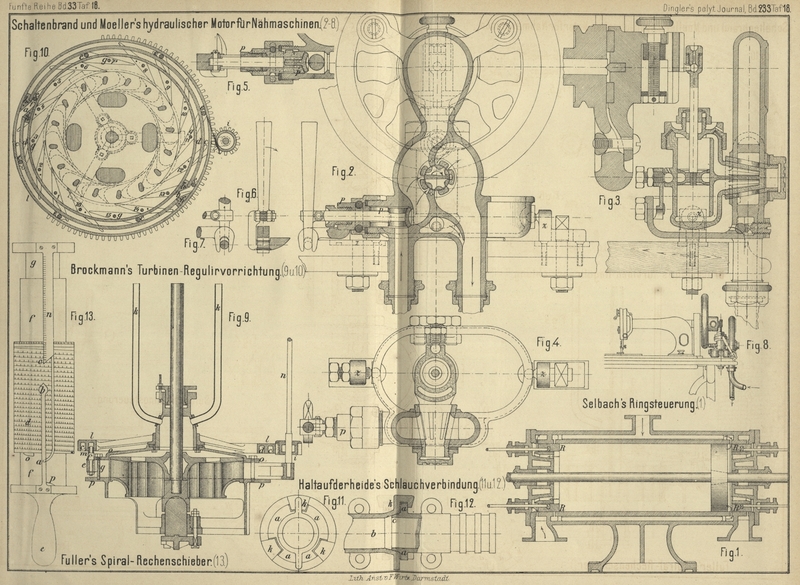
Fuller's Spiral-Rechenschieber.
Da man dem gewöhnlichen geraden Rechenschieber aus praktischen Rücksichten höchstens
eine Länge von ungefähr 0m,6 und dem kreisförmigen
einen Durchmesser von etwa 200mm geben darf, so
ist die Zahl der Theilstriche eine sehr beschränkte. Bei dem in Fig. 11
Taf. 18 dargestellten Instrumente hat nun Prof. G.
Füller am Queen's College zu Belfast den glücklichen Gedanken verwirklicht,
die Scale schraubenförmig um einen Cylinder zu winden, wodurch er über eine
Scalenlänge von 12m,7 verfügt, welche eine
Theilung in 7250 Theile gestattet, ohne daſs die Striche zu gedrängt stehen.
Das Instrument besteht aus einem hohlen Holzcylinder d,
welcher inwendig mit einem wollenen Stoff ausgefüttert ist, damit er unter sanfter
Reibung auf dem mit einer Handhabe e und einem festen
Zeiger b versehenen, gleichfalls hohlen Cylinder f sich verschieben lasse. Auf dem Cylinder d ist die logarithmische Scale in einer Schraubenlinie
markirt, während auf dem Cylinder f eine Anzahl nützlicher Hilfstabellen
zu gelegentlichem Gebrauche angeordnet ist. Ein innerhalb des Cylinders
verschiebbarer Kolben g trägt einen Arm n mit zwei Zeigern a und
e, deren Abstand der achsialen Länge der
Schraubenscale gleich ist.
Um mit dem Instrumente z.B. zu multipliciren, stellt man zunächst den Index b dadurch auf den Anfang der Schraubenscale, daſs man
die an dem Schieber d angebrachte Nase o mit dem Vorsprung p an
der Basis des Cylinders f in Berührung bringt. Dann
stellt man den beweglichen Zeiger auf den Multiplicanden und den festen Zeiger durch
Verschiebung des Cylinders d auf den Multiplicator,
worauf das Product an einem der beweglichen Zeiger abgelesen werden kann. Mit Hilfe
einer an dem Index n und einer auf dem Schieber
oberhalb der logarithmischen Theilung aufgetragenen Scale ist zugleich die
Potenzirung und Radicirung einer Zahl ermöglicht. (Nach Engineering, 1879 Bd. 27 S. 257.)
Tafeln