| Titel: | Ueber Temperaturmessungen. |
| Autor: | F. |
| Fundstelle: | Band 233, Jahrgang 1879, S. 400 |
| Download: | XML |
Ueber Temperaturmessungen.
Mit Abbildungen auf Tafel 37.
Ueber Temperaturmessungen.
Bestimmung der wahren Lufttemperatur von H. Wild. Wenn
man sieht, wie häufig in den zur Bestimmung der Lufttemperatur getroffenen
Einrichtungen fehlgegriffen wird, so muſs man annehmen, daſs nicht immer eine blose
Nichtachtung der hierbei in Betracht kommenden physikalischen Gesetze, sondern
ebenso oft wohl auch eine Unklarheit über die zu bestimmende Gröſse selbst die
Ursache hiervon ist.
Der Physiker bezeichnet der mechanischen Wärmetheorie entsprechend
die Temperatur eines Gases als lebendige Kraft der als Wärme aufgefaſsten
unsichtbaren Bewegungen der Molecüle derselben. Concreter aufgefaſst, ist Temperatur
einer bestimmten Menge trocknen Gases die Gröſse, welche bei freier Expansion
desselben neben dem äuſseren Druck den Volum- und Dichtigkeitszustand desselben nach
dem Dalton-Gay-Lussac'schen Gesetz bedingt, oder bei constantem Volum des Gases dem
letzteren zufolge die Spannkraft desselben verändert. Abgesehen von gewissen
Correctionen ist daher beim Luftthermometer die gehobene Quecksilbersäule im offenen
Schenkel ein genaues Maſs der Temperatur des im Gefäſs bis zur Marke
eingeschlossenen, auf constantem Volum erhaltenen Gases. In der Meteorologie hat man
dem entsprechend unter der Temperatur der freien Luft nur die Gröſse zu verstehen,
welche, abgesehen von beigemengtem Wasserdampf, Kohlendioxyd u. dgl., allein neben
dem äuſseren Druck die jeweilige Dichtigkeit derselben bedingt. Die Dichtigkeit der
Luft unter Berücksichtigung der Druck- und Zusammensetzungsverhältnisse derselben
wird also hier als Maſs ihrer Temperatur dienen können.
Das Luftthermometer läſst nun zwar mit Sicherheit die Temperatur
der in sein Gefäſs eingeschlossenen Luft messen; man. würde aber, wie H. Wild im Repertorium für
Meteorologie, 1879 Bd. 6 Nr. 9 ausführt, im Allgemeinen sehr irren, wenn
man annehmen wollte, daſs dasselbe zugleich auch die Temperatur der freien das
Gefäſs umgebenden Luft anzeige. Die festen Substanzen, welche bei allen
Thermometern, sei es, wie hier, als Gefäſs zur Aufnahme der durch die Wärme sich
ausdehnenden gasförmigen oder tropfbaren Flüssigkeit, sei es direct, wie bei den
Metallthermometern, thermo-elektrischen Ketten oder den elektrischen
Widerstandsthermometern, zur Anwendung kommen, besitzen alle ein. viel gröſseres
Absorptions- und Ausstrahlungsvermögen für die Wärmestrahlen als die Luft, und, da
sich jeder Körper durch gegenseitige Wärmestrahlung mit seiner ganzen Umgebung in
Beziehung setzt, so kann es sehr leicht geschehen, daſs der in die Luft eingetauchte
thermometrische Körper in Folge dieser Verschiedenheit der Strahlung eine ganz
andere Temperatur als jene hat.
Das einzige Mittel, die Temperatur der Luft frei von dieser
Fehlerquelle zu bestimmen, besteht darin, ihre Dichtigkeit zu messen. Der Gewichtsverlust in Milligramm, welchem ein am
einen Arm einer Wage angehängter Glasballon vom äuſsern Volum F Liter in
gewöhnlicher, Kohlensäure haltiger, feuchter Luft an einem H Meter über dem Meer und unter der Breite φ
gelegenen Orte erleidet, ist gegeben durch:
G=V\,\frac{h-0,378\,h'}{760\,(1+0,003665\,t)\,(1293,03-3,32\ cos\
2\varphi-0,00027\,H)},
wo h der auf 0° reducirte
Barometerstand, h' die absolute Feuchtigkeit der Luft,
beide in Millimeter, und t die gesuchte Temperatur der
vom Glasballon verdrängten Luft ist.
Da die Ausdehnung der Luft etwa 100 Mal so groſs ist als die des
Glases, so zeigt t die Temperatur der umgebenden Luft
unabhängig von der etwa durch Strahlungseinflüsse geänderten eigenen Temperatur des Glasballons. Letztere
beeinfluſst nur das Volum V und kann leicht für sich
bestimmt und in Rechnung gebracht werden. Setzt man nun
h=760^{mm}, \varphi=45°,
H=0 und V=10^l, so ergibt sich
G=\frac{1-0,000497\,h'}{1+0,003665\,t}\,12930^{mg}. Hieraus
folgt durch Differentiation mit genügender Annäherung: dG=12930\times
0,000497\,dh' und dG=12930\times 0,003665\,dt.
Wenn also die Genauigkeit der Gewichtsbestimmung:
dG=\pm\,1^{mg} ist, so wird man bei der Bestimmung der
absoluten Feuchtigkeit einen entsprechenden Fehler
dh'=\pm\,0^{mm},16 begehen dürfen und die Temperatur der Luft
mit einer Sicherheit von dt=\pm\,0,021° erhalten, da alle übrigen
Gröſsen des obigen Ausdruckes mit groſser Genauigkeit zu bestimmen sind. Das gröſste
Hinderniſs für die Ausführung dieser Methode der Temperaturbestimmung bildet
jedenfalls die Bestimmung der absoluten Feuchtigkeit h'
die beim gegenwärtigen Zustand der Hygrometrie kaum mit einer Sicherheit von
\pm\,0{mm},16 zu erzielen ist. Aber auch dann, wenn diese
Schwierigkeit überwunden sein wird, werden die schwierigen Operationen, welche diese
Methode erfordert, nur eine Verwerthung derselben bei vereinzelten
Fundamentaluntersuchungen gestatten.
Für gewöhnlich wird man daher doch Thermometer zur Bestimmung der Lufttemperatur
verwenden müssen. Um nun den störenden Einfluſs der Sonnenstrahlen, sowie der
Ausstrahlung gegen den kalten Weltraum und den festen Erdboden zu vermeiden,
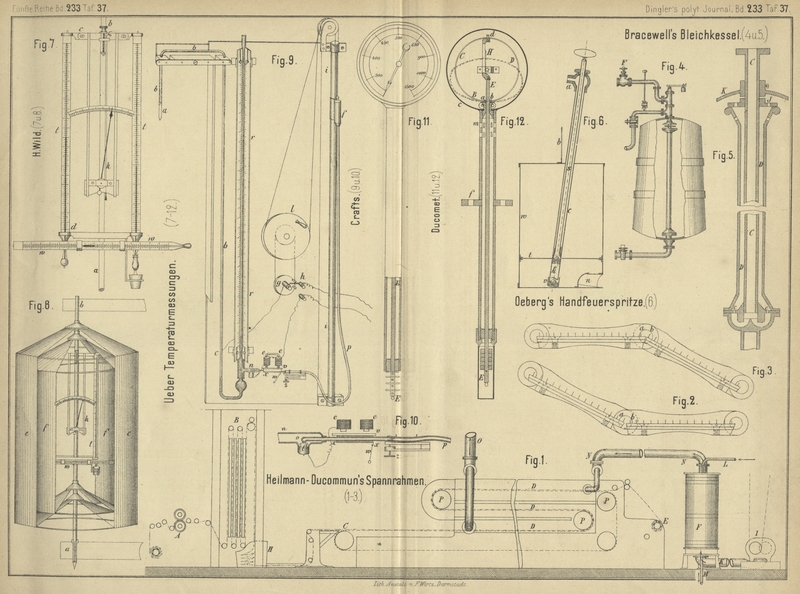
empfiehlt H. Wild an einem unten mit einer Schraube
versehenen runden Eisenstabe ab (Fig. 7 und
8 Taf. 37) mittels der beiden verschiebbaren Querstücke c und d die zwei
Psychrometerthermometer f, das Haarhygrometer h und das Weingeist-Minimumthermometer w zu befestigen. Nach auſsen werden diese Instrumente
von den zwei halb offenen Zinkblechcylindern e und f mit conischem Dach und nach innen zu ansteigendem
conischem Boden umhüllt. Um bequem ablesen zu können, wird der äuſsere kreisförmige
Cylinder e so gedreht, daſs seine gegenüber liegenden
Oeffnungen sich mit denen des inneren elliptischen Cylinders f decken, wie Fig. 8
zeigt, während sie in der übrigen Zeit zur Abhaltung der Strahlung so gestellt
werden, daſs die Oeffnungen des inneren durch die Wände des äuſseren Cylinders
verdeckt sind; dasselbe ist dann auch der Fall mit den entsprechenden Oeffnungen des
conischen Daches und Bodens. Durch die breiten Zwischenräume zwischen den Cylindern
sowohl an den Seitenwänden, wie im Dach und Boden ist auch bei dieser Stellung für
genügend freien Luftwechsel gesorgt. Das Gehäuse wird vor einem nach Norden
gewendeten Fenster befestigt, oder in einer besonderen Holzhütte aufgestellt.
Nach den Versuchen von H. Wild erhält man mit diesem
Thermometergehäuse die wahre Lufttemperatur mit einer Sicherheit von mindestens ±
0,1°; ja selbst die relative Feuchtigkeit der Luft wird, wenn man auſser der
Temperatur auch diese bestimmen will, durch diese Vorrichtung im Durchschnitt bis
auf 3 Proc. genau angegeben gegenüber einem frei aufgestellten Psychrometer.
Neue Form des Luftthermometers von J. M. Crafts. Dieser
in Fig. 9 und 10 Taf. 37
nach den Annales de Chimie et de Physique, 1878 Bd. 14
S. 409 dargestellte
Apparat ist – dem von Jolly (vgl. 1877 225 275) entsprechend – ein Luftthermometer mit
constantem Volum. Der kleine, mit Wasserstoff gefüllte, nur 0cc,75 fassende Behälter a ist durch das 0cc,023 fassende, 84cm lange Capilfarrohr b mit dem Manometer r und durch den Schlauch
p mit dem Quecksilbergefäſs f verbunden. Letzteres ist mittels der über die Rolle l gehenden Schnur auf dem Rohre i verschiebbar, in welchem am anderen Ende der Schnur ein entsprechendes
Gegengewicht hängt.
Eigenthümlich ist der in Fig. 10 im
Durchschnitt dargestellte Quecksilberabschluſs. Das durch den Schlauch p zuflieſsende Quecksilber tritt bei o aus einer kleinen Oeffnung des in das Rohr n mittels Kautschukschlauch luftdicht eingesetzten
Rohres x zum Manometer. Die Oeffnung o legt sich auf das obere, mit einer Gummischeibe
überzogene Ende des eingekitteten Rohrendes t, neben
welchem ein nach dem Elektromagnete e führender
Platindraht eingeführt ist, während der andere Draht bei c eingeschmolzen wurde. Das Rohr x ist ferner
in einer Kupferröhre befestigt, welche die dem Elektromagnete als Anker gegenüber
gestellte Eisenplatte v trägt, deren Einstellung
mittels der Schraube z bewirkt wird. Soll Quecksilber
eintreten, so zieht man an der Schnur w, während sonst
mittels eines auf der Scheibe g befestigten, an h anliegenden Stiftes der Strom und somit in Folge der
Hebung des Rohres x durch den Elektromagnet die
Oeffnung o geschlossen wird.
Bestimmung hoher Temperaturen durch Aenderung des
Aggregatzustandes. Die schon von Prinscep
(1828 28 421) vorgeschlagene Verwendung verschiedener
Metalle und Legirungen zur Bestimmung hoher Temperaturen (vgl. 1877 225 276) sucht J. Documet in
Paris (*D. R. P. Nr. 4882 vom 11. September 1878) in folgender Weise auszunutzen.
Die beiden Enden der von einem Gehäuse eingeschlossenen Feder BCD (Fig. 11 und
12 Taf. 37) werden durch die kleinen Schrauben a und b der Führungsbüchse c festgehalten. Durch die Schraube d ist die Feder mit der Zahnstange H verbunden, welche in ein kleines Getriebe eingreift,
auf dessen Achse ein Zeiger sitzt, der somit durch eine Verschiebung der aus Metall
oder feuerfestem Thon hergestellten Stange E bewegt
wird. Das untere Ende dieser durch eine Metallhülle geschützten Stange trägt eine
Anzahl Scheiben von verschiedenem Schmelzpunkt, durch deren Gewicht die Feder etwa
in die angedeutete elliptische Form gezogen wird. Erreicht nun die Temperatur des
bis zur Flansche f der zu messenden Hitze ausgesetzten
unteren Theiles den Schmelzpunkt einer der Platten, so schmilzt diese ab, die Feder
wird dadurch entsprechend entlastet und rückt den Zeiger vor. Wie Fig. 11
zeigt, kann man statt der Platten auch Stifte durch die Stange E stecken, bei deren Abschmelzen die Stange und somit auch der Zeiger
entsprechend vorrückt. Es läſst sich ferner unten an die Stange eine Schale hängen,
die mit einer Flüssigkeit gefüllt wird, durch deren Verdampfung aus den Oeffnungen
m (Fig. 12)
die Feder entlastet wird u.s.f. – Das Verfahren dürfte nur für wenige Fälle
empfehlenswerth sein.
W. Roberts (Annales de Chimie
et de Physique, 1878 Bd. 13 S. 111) hat die Schmelzpunkte einer Reihe von
Silber-Kupferlegirungen bestimmt, leider aber in so unvollkommener Weise, daſs seine
Angaben für Temperaturmessungen nicht verwendbar sind.
Th. Erhard und A. Schertel
haben nach dem Jahrbuch für das Berg- und Hüttenwesen im
Königreich Sachsen, *1879 S. 17 die Schmelzpunkte einiger Legirungen von
Silber, Gold und Platin mittels eines Luftthermometers in einem kleinen, mit einem
Schlösing'schen Löthrohre geheizten Ofen bestimmt. Zur Herstellung der Legirungen
wurden die Metalle abgewogen und, in Mengen von 100 bis 150mg zur Kugel geschmolzen, der zu messenden Hitze
ausgesetzt. Die Platin-Goldlegirungen zeigten groſse Neigung zum Entmischen. Die
Verfasser glauben, daſs diese bis 1400° gehenden Bestimmungen nur eine Ungenauigkeit
bis 20° zeigen; die höheren Temperaturen sind mit Benutzung der Angaben von J. Violle (1878 227 108. 230 325) durch graphische Interpolation gefunden:
Zusammen-setzungProc.
Schmelz-punkt
Zusammen-setzungProc.
Schmelz-punkt
Zusammen-setzungProc.
Schmelz-punkt
Silber = Ag
954°
80 Au 20 Pt
1190°
35 Au 65 Pt
1495°
80 Ag 20 Au
975
75 25
1220
30 70
1535
60 40
995
70 30
1255
25 75
1570
40 60
1020
65 35
1285
20 80
1610
20 80
1045
60 40
1320
15 85
1650
Gold = Au
1075
55 45
1350
10 90
1690
95 Au 5 Pt
1100
50 50
1385
5 95
1730
90 10
1130
45 55
1420
Platin = Pt
1775
85 15
1160
40 60
1460
Mit Hilfe dieser Tabelle haben Erhard und Schertel die von Plattner
i. J. 1840 veröffentlichten Schmelzpunktbestimmungen einer Reihe verschiedener
Schlacken umgerechnet, auch selber einige Bestimmungen ausgeführt, von denen
folgende angeführt werden mögen:
Kupfer
Schmelzpunkt bei
1100°
Malaphyr von Mulatto
„ „
1106
Pechstein von Arrom
„ „
1106
Hauynbasalt von Neudorf b. Annaberg
Schmelzpunkt zwischen 1080 u.
1106
Leucitbasalt vom Bohlberg bei Annaberg
Schmelzpunkt bei
1130
Syenit von Edle Krone bei TharandPechsteinporphyr von
LeisnigQuarzporphyr aus dem Travignothale
Schmelzpunkt zwischen 1130 und
1160
Asbest
Schmelzpunkt ungefähr
1300
Scharffeuer des Porzellanofens (Meiſsner Fabrik)
Schmelzpunkt bei
1460
Nach den Versuchen von J. Violle
(Comptes rendus, 1878 Bd. 87 S. 981) schmilzt
Palladium bei 1500°, mit einer latenten Schmelzwärme von 36,3. Die mittlere
specifische Wärme zwischen 0° und t° beträgt:
t
t
t
100
=
0,0592
500
=
0,0632
900
=
0,0672
200
=
0,0602
600
=
0,0642
1000
=
0,0682
300
=
0,0612
700
=
0,0652
1200
=
0,0702
400
=
0,0622
800
=
0,0662
1300
=
0,0712,
entspr. der Formel 0,0582 + 0,00001 t; die wahre specifische Wärme ist = 0,0582 + 0,00002 t, somit bei 0° = 0,0582, bei 1000° == 0,0782.
Das Pyrometer von J. B. v.
Saintignon besteht nach dem Englischen Patent Nr. 2409 vom 17. Juni 1878
aus einem der zu messenden Temperatur ausgesetzten Porzellanrohr, durch welches
Wasser geleitet wird. Aus der Wärmeaufnahme desselben wird durch Multiplication mit
einer für jedes Rohr festgestellten Zahl die Temperatur berechnet. – Da es
mindestens zweifelhaft ist, daſs die Wärmeübertragung der Temperaturdifferenz genau
proportional ist, so verdienen die mit diesem Apparat erhaltenen Angaben wenig
Vertrauen.
Thermodynamometer. R. Pictet benutzt unter Anwendung
des zweiten Hauptsatzes der mechanischen Wärmetheorie zur Temperaturmessung durch
die mechanische Arbeit die Spannungen verschiedener Dämpfe, welche einerseits in
einer festen Beziehung zu den Temperaturänderungen stehen, andererseits in dem auf
die Gefäſswände ausgeübten, mittels Manometer meſsbaren Druck einen in
Meterkilogramm darstellbaren Werth liefern. Für Temperaturen von – 180 bis – 100°
benutzt er eine Mischung aus gleichen Theilen Kohlensäure und Stickoxydul, von – 100
bis – 40° reine Kohlensäure, von – 40 bis + 25° reine Schwefligsäure, von + 25 bis +
900 Aether und von + 90 bis 200° Wasser. Bezüglich des Apparates und der umfassenden
Berechnungen, welche diese für technische Zwecke wohl nicht brauchbaren
Temperaturbestimmungen erfordern, muſs auf die ausführliche Abhandlung in den Archives des Scienses physiques et naturelles, *1878
Bd. 64 S. 185 verwiesen werden.
Spectroskopische Messung hoher Temperaturen. A. Crova
(Comptes rendus, 1878 Bd. 87 S. 879) bestimmt aus
den continuirlichen Spectren zweier Lichtquellen, deren eine die bekannte Temperatur
T, die andere die unbekannte t hat, mittels Spectrometer die Intensität eines rothen
und eines grünen Strahles, deren Wellenlängen λ und λ1 676 und 523
betragen. Der Quotient derselben gibt das Verhältniſs der Intensitäten der Strahlen
λ1 in beiden
Spectren, wenn das stärkere so abgeschwächt wurde, daſs der Strahl λ in beiden gleich ist. Zwei Körper desselben
Strahlungsvermögens haben aber dieselbe Temperatur, wenn die Intensitäten der
einfachen Strahlen ihrer continuirlichen Spectren gleich bleiben, falls das stärkere
durch zwei Nicols so geschwächt wird, daſs die Intensitäten zweier Strahlen gleicher Wellenlänge in
beiden Spectren gleich sind. Crova gibt nun dem Lichte
einer mit Rüböl gespeisten Moderateurlampe die optische Temperatur 1000 und
vergleicht damit die Intensitäten des grünen und rothen Strahles der unbekannten
Lichtquelle. Das so erhaltene Verhältniſs wird mit dem Strahlungsvermögen des
Porzellanbehälters eines Luftthermometers verglichen und so auf die richtige
Temperatur umgerechnet. Wie Becquerel (vgl. 1877 225 278) für Porzellan, Kohle, Platin und Magnesia, so
hat Crova für Kohle, Kalk und Platin gleiches
Strahlungsvermögen gefunden.
Setzt man nach den Versuchen von J.
Violle (Comptes rendus, 1879 Bd. 88 S. 171)
die Intensität I des von Platin beim Schmelzpunkt des
Silbers (954°) ausgestrahlten Lichtes = 1, so erhält man für die Temperaturen
zwischen 800 und 1775° folgende Werthe:
800°
I =
0,108
1200°
I =
17,8
1600°
I =
327
900
0,475
1300
45,2
1700
481
1000
1,82
1400
100
1775
587
1100
6,10
1500
194
Diese der Formel log I = –
8,244929 + 0,0114751 t – 0,000002969 t2 entsprechenden
Zahlen zeigen, daſs das bei 500° kaum, sichtbare rothe Licht anfangs rasch, dann
langsam zunimmt, bei 1933° das Maximum von 696 erreicht, um bei 2910° wieder auf 1
herunter zu gehen. Die Intensität einer bestimmten Strahlung wächst somit nicht
unbegrenzt mit der Temperatur, sondern wird bei einer gewissen hohen Temperatur
gerade so wieder unmerklich, als sie bei einer anderen niederen Temperatur erst
auftrat.
F. Rosetti (Beiblatt zu den
Annalen der Physik, 1878 S. 695) fand das Strahlungsvermögen – das des
erhitzten, mit Ruſs bedeckten Kupfers = 1 gesetzt – von Kupfer = 0,943, von Eisen =
0,882, von Platin 0,35 und von Magnesiumoxychlorid 0,58.
J. L. Soret zeigt im Naturforscher, 1879 S. 115, daſs das Gesetz von Dulong und Petit für hohe Temperaturen keine
Giltigkeit hat. Läſst man nämlich einen elektrischen Strom durch einen leitenden
Draht gehen, so steigt die Temperatur desselben bis zu dem Grade, daſs die Wärme,
welche er durch Strahlung, durch die Berührung mit der Luft und durch die Leitung an
den Befestigungspunkt verliert, gleich ist der Wärme, welche die Elektricität in
seinem Innern entwickelt. Man kann nun einerseits diese Wärmemenge berechnen,
andererseits, indem man die Temperatur schätzt, welche der Draht annimmt, die
Wärmemenge bestimmen, die er nach dem Dulong und Petit'schen Gesetze ausstrahlen
muſs. Ein 0mm,32 dicker und 385mm langer Platindraht, dessen Oberfläche somit
385qmm betrug, wurde nun durch den Strom einer
dynamo-elektrischen Maschine von 42c,3
Wärmeentwicklung in der Minute zum Schmelzen gebracht, während schon die Oberfläche
von 3qcm bei 1700° nach der Dulong und Petit'schen
Formel in der Minute
146c ausstrahlen sollte, was nicht möglich
ist, da höchstens 42c zugeführt wurden. – Die
letzterwähnten Temperaturbestimmungen durch Vergleichung der Wärme- oder
Lichtstrahlen sind daher vorläufig noch mit Vorsicht aufzunehmen.
F.
Tafeln