| Titel: | Ueber Ringspinnmaschinen mit variabler Spindelgeschwindigkeit. |
| Autor: | A. Lüdicke |
| Fundstelle: | Band 240, Jahrgang 1881, S. 265 |
| Download: | XML |
Ueber Ringspinnmaschinen mit variabler
Spindelgeschwindigkeit.
Mit Abbildungen auf Tafel 22.
Ueber Ringspinnmaschinen mit variabler
Spindelgeschwindigkeit.
Das Bulletin de la Société industrielle de Mulhouse,
1880 Bd. 50 S. 437 bringt einen längeren von P. Dupont,
Professor an der Schule für Spinnerei – und Webereitechniker in Mülhausen, und V. Schlumberger verfassten Artikel über
Ringspinnmaschinen, welcher in Bezug auf Beschreibung neuerer Maschinen viel
Beachtenswerthes enthält, so daſs eine theilweise Wiedergabe in diesem Journal
geboten erscheint. Dagegen vermiſst Referent sehr, daſs von den genannten Verfassern
nicht der Versuch gemacht worden ist, die Theorie der Maschine etwas weiter
auszuführen und für die Berechnung der Geschwindigkeiten u.s.w. nutzbar zu machen.
Das Nachstehende gibt eine vielleicht willkommene Ergänzung des obiger Quelle
entstammenden Berichtes.
In dem Artikel wird zunächst – nachdem darauf hingewiesen ist,
daſs in Folge des veränderlichen Durchmessers der Spule bei constanter
Geschwindigkeit derselben die Fadenspannung veränderlich ist – eine Formel
entwickelt, welche Aufschluſs geben soll über die Abhängigkeit beider von einander.
Ist die Spannung in dem vom Läufer nach der Spule laufenden Fadenstück (Fig.
1 Taf. 22) = P, der Spulenhalbmesser ac = r, der Ringhalbmesser ab
= ρ so ist die den Läufer im Punkte b
erfassende und in Bewegung setzende Tangentialkraft:
T=P\,sin\,\alpha=P\,\frac{r}{\varrho}.
Setzt man hierin T
constant, so ist die Fadenspannung dem Spulenhalbmesser umgekehrt proportional; bei
constanter Fadenspannung wäre die für den Betrieb des Läufers zur Verfügung stehende
Kraft direct proportional dem Spulenhalbmesser. Soweit der Bericht a. a. O.
Die gewöhnliche Construction der Ringbänke bedingt, wie Referent
in einer kleinen, im Civilingenieur, 1880 Heft 6 und 7
veröffentlichten Abhandlung nachgewiesen hat, sehr starke und an den Enden des
Ringbankweges sogar plötzliche Aenderungen der Fadenspannung. Die Grenzen derselben
rücken um so weiter aus einander, je gröſser der Unterschied zwischen gröſstem und
kleinstem Spulenhalbmesser ist. Um die Fadenspannung in erträglichen Grenzen zu
halten, wurde das Garn bisher fast allgemein auf Holzspulen gewunden. Könnte man die
Fadenspannung constant halten, so wäre damit ein ganz bedeutender Vortheil erreicht,
vorausgesetzt, daſs dadurch nicht andere Uebelstände herbeigeführt würden. Es
lieſsen sich dann auf der Ringbank nicht allein Garne mit geringerem Drahte als
bisher spinnen; man könnte auch das Garn auf Papierdütchen aufwickeln, wodurch der
Inhalt des Garnkörpers beträchtlich wächst. Die theueren Holzspulen würden erspart;
die Abzüge erfolgten in längeren Zwischenräumen und die Lieferung der Maschine würde
zunehmen.
Zur Beantwortung der Frage: wie läſst sich die Fadenspannung
constant halten, muſs man sich zunächst darüber klar werden, welche Kräfte auf den
Läufer einwirken, um die der Bewegung entgegenstehenden Widerstände ermitteln zu
können. Ein Blick auf Fig. 1 und
2 gibt darüber Aufschluſs. In radialer Richtung wirken: Centrifugalkraft
= C und die Componente P cos
α, senkrecht abwärts das Gewicht des Läufers = G und in Richtung des vom Fadenführer o kommenden
Fadens die Spannung Q. Wie aus den Figuren ersichtlich,
ist angenommen worden, daſs der Faden vom Führungsauge nach dem Läufer in gerader
Linie läuft, während er sich in Wirklichkeit ausbaucht, und daſs das zwischen Läufer
und Spule ausgespannte Fadenstück in einer wagrechten Ebene liegt, während es
tangential zu der vom Faden auf der Kötzeroberfläche beschriebenen Schraubenlinie
läuft. Wollte man beides berücksichtigen, so würde man zu sehr zusammengesetzten
Verhältnissen kommen. Der durch obige Annahme etwa erwachsende Fehler wird auſserdem
sehr klein sein.
Die vier Kräfte Q, C, G und P cos α liegen in einer durch die Spindelachse gehenden
Ebene. Ihre Resultante R steht senkrecht zur Tangente
an den Ring im Punkte b. Multiplicirt man R mit dem Coefficienten der Reibung f zwischen Läufer und Ring, so ist damit der Widerstand
des Läufers gegeben, wenn man von den wohl kaum zu ermittelnden Luftwiderständen
absieht und davon, daſs der Läufer während des Ganges wahrscheinlich eckt. Für den
Beharrungszustand muſs hiernach folgende Gleichung bestehen:
R\,f=P\,sin\,\alpha . . . . . . (1)
Sind P, f und α bekannt und soll P für
alle Spulenhalbmesser constant bleiben, so muſs die Centrifugalkraft veränderlich
sein. Diese läſst sich nunmehr leicht auf graphischem Wege ermitteln, wenn man das
Läufergewicht, welches im Verhältniſs zur Centrifugalkraft immer sehr klein ist,
vernachlässigt und noch Q = P setzt. P ist in Wirklichkeit gröſser als
Q; denn der Faden findet bei dem Durchgang durch
den Läufer Reibungswiderstand. Die Gröſse des letzteren entzieht sich zur Zeit noch
genauer Angabe. Der Unterschied zwischen P und Q ist aber aller Wahrscheinlichkeit nach gering.
Zur Bestimmung der Centrifugalkraft trägt man in Fig. 3 vom
Punkte b aus nach rechts P cos
α auf, in Richtung der Linie bo die Gröſse P. Die Resultante beider ist R1. Nimmt man nun den aus Gleichung (1)
berechneten Werth von R in den Zirkel und schlägt von
b aus einen Kreisbogen, welcher die durch den
Endpunkt von R1
gezogene Parallele zu ba in d schneidet, und zieht durch d eine Parallele
de zu R1 so schneidet diese auf ba die Strecke be = C ab.
Die augenblickliche Umdrehungszahl u
des Läufers, welche C entspricht, folgt aus der
Gleichung:
u=\sqrt{894,454\frac{C}{G\,\varrho}}, .
. . . . . . (2)
worin C und G in Kilogramm, q in Meter
einzusetzen ist.
Leider ist weder die Spannung des Fadens während des Spinnens,
noch der Reibungscoefficient f bekannt. Verfasser hat,
um sich einigen Aufschluſs über die Gröſse des Reibungscoefficienten zu verschaffen,
folgenden Weg eingeschlagen: Kennt man die Werthe G und
ρ der Gleichung (2), so findet sich die
Centrifugalkraft:
C=\frac{u^2}{894,454}\,G\,\varrho. . .
. . . . . (3)
C wird für verschiedene
Werthe von u berechnet und nun unter Zugrundelegung
verschiedener Werthe von P mit Hilfe von Fig.
3
R construirt. Dann findet sich aus Gleichung (1):
f=\frac{P}{R}\,sin\,\alpha . . . . . .
. (4)
Für die Berechnung nachstehender Tabelle wurden folgende einer
Ringspindel der technologischen Sammlung des Braunschweiger Polytechnikums
entnommenen Werthe zu Grunde gelegt: Mittlerer Ringhalbmesser ρ = 22mm,225 (⅞''
engl.), gröſster Spulenhalbmesser r1 = 15mm,875
(⅝''), Abstand der Ringbank vom Läuferauge s = 254mm (10''). Bei dem Spinnen von Garn Nr. 16 beträgt
das Gewicht des Läufers 0g,1. Das Zerreiſsgewicht
eines auf der Ringspindel gesponnenen Baumwollgarnes Nr. 16 der genannten Sammlung
beträgt 470g.
Umdrehungen des Läufers u = 5000
6000
7000
8000
Fadenspannung P
= 5g
f = 0,06
0,047
0,0297
0,0226
10
f = 0,128
0,086
0,062
0,047
20
f = –
–
0,132
0,099
30
f = –
–
–
0,154
40
f = –
–
–
0,216
50
f = –
–
–
0,280
Die Tabelle ist berechnet unter der Voraussetzung, daſs der Faden
gegen den gröſsten Spulendurchmesser anläuft, d.h., daſs der Läufer die gröſste
Umdrehungszahl besitzt.
Der Coefficient der gleitenden Reibung zwischen polirtem Stahl auf
polirtem Stahl ohne Schmierung liegt sicher unter 0,2. Berücksichtigt man, daſs u > 8000 (u ist
Umdrehungszahl des Läufers) nur selten vorkommen wird, daſs für f = 0,1 und u = 8000 der
Werth P ohne die gewiſs nicht geringen Luftwiderstände
= 20g ist, so wird man wohl nicht sehr
fehlgreifen, wenn man f zu 0,1 annimmt. Die Spannung
P = 20g erscheint
im Verhältniſs zur Zerreiſsfestigkeit des fertigen Garnes gering. Der Faden befindet
sich aber noch in der Bildung und ist dabei mehr oder weniger groſsen
Erschütterungen ausgesetzt. Eine geringe Spannung kann nur vortheilhaft sein; es
werden um so weniger Fadenbrüche auftreten.
Wird also f = 0,1 angenommen und soll
die Fadenspannung P = 20g für 16er Baumwollgarn constant gehalten werden, so lassen sich jetzt aus
dem gröſsten Spulenhalbmesser r1, dem kleinsten r2 = 4mm,76 (3/16'' engl.) die
entsprechenden Umdrehungszahlen u1 und u2 des Läufers bestimmen. Es ist bei Bewickelung
auf:
r_1
r_2
sin\,\alpha=\frac{r_1}{\varrho}=\frac{^5/_8}{^7/_8}=0,71428
sin\,\alpha\,\frac{r^2}{\varrho}=\frac{^3/_{16}}{^7/_8}=0,21428
R=\frac{P}{f}\,sin\,\alpha=\frac{20}{0,1}\,sin\,\alpha=142^g,857.
R=42^g,856.
Nunmehr kann man die Centrifugalkraft
auf oben beschriebene Weise construiren und mit Hilfe von Gleichung (2) den Werth
u berechnen. Es ist
C=157^g,0
C=59^g,5
u_1=7953\ \mbox{rund}\ 7950.
u_2=4896\ \mbox{rund}\ 4900.
Ist noch der Drahtcoefficient φ
bekannt (Zahl der Drehungen auf 1'' engl.
=\varphi\,\sqrt{\mbox{Garnnummer}}), so lassen sich die
äuſsersten Grenzen der Spindelumdrehungen n1 und n2 ermitteln.
Macht der Läufer u1 Umdrehungen in 1 Minute, so muſs das Streckwerk,
wenn durch das Zusammendrehen des Fadens weder Verlängerung, noch Verkürzung
eintritt, in derselben Zeit
\frac{u_1}{\varphi\,\sqrt{\mbox{Nr.}}}. Zoll Garn
herausgeben. Um diese Länge aufzuwinden, muſs die Spindel, da auf den Halbmesser r1 gewunden wird,
\frac{u_1}{2\,r_1\,\pi\,\varphi\,\sqrt{\mbox{Nr.}}} Drehungen
mehr machen als der Läufer. Es ist demnach:
n_1=u_1+\frac{u_1}{2\,r_1\,\pi\,\varphi\,\sqrt{\mbox{Nr.}}}=u_1\,\left(1+\frac{1}{2\,r_1\,\pi\,\varphi\,\sqrt\mbox{Nr.}}\right).
Ebenso findet sich, wenn auf den kleinsten
Spulenhalbmesser gewunden wird:
n_2=u_2\left(1+\frac{1}{2\,r_2\,\pi\,\varphi\,\sqrt{\mbox{Nr.}}}\right)
u_1=7950,\ r_1={^5/_8}'',\ \varphi=3,5,\ \mbox{Nr.}\
16:
u_2=4650,\ r_2={^3/_{16}}'',\ \varphi=3,5,\ \mbox{Nr.}\
16:
n_1=8020.
n_2=5190.
Durch Ausrechnen einiger Zwischenwerthe ist die in Fig.
3 verzeichnete Curve f g h der
Spindelumdrehungen erhalten werden.
Die Bildung des Garnkörpers erfolgt bei Ringbänken in derselben
Weise wie bei Mulemaschinen. Es liegen aber in der von der Spitze nach der Basis
gewundenen Schicht ½ bis ⅓ so viel Windungen als in der von der Basis nach der
Spitze gewundenen. An dem Probekötzer war w1
= 22 und w2 = 66. Die Garnlängen in den einzelnen Schichten
sind hiernach:
L_1=w_1\,\frac{r_1+r_2}{2}\,2\,\pi=56,128'' und
L_2=w_2\,\frac{r_1+r_2}{2}\,2\,\pi=168,382''.
Um nun noch die Zeit zu ermitteln, welche für einen Aufgang
bezüglich Niedergang der Ringbank erforderlich ist, wurde angenommen, daſs das Garn
auf einen Cylindermantel vom Halbmesser ½ (r1 + r2) aufgewunden werde und sich die Ringbank
gleichförmig bewege. Bei Bewickelung auf den Halbmesser ½ (r1 + r2) macht der Läufer, wie durch Rechnung zu finden,
6530 Umdrehungen; folglich muſs das Streckwerk in jeder Secunde:
l=\frac{6530}{60\,\varphi\,\sqrt{\mbox{Nr.}}}=7,774''
engl.
Garn herausgeben. Dividirt man mit l in die in den einzelnen Schichten liegenden
Garnlängen, so erhält man die Zeit für einen
Niedergang der Ringbank:
Aufgang der Ringbank:
t_1=\frac{L_1}{l}=7,2\
\mbox{Sec.}
t_2=\frac{L_2}{l}=21,6\
\mbox{Sec.}
In Wirklichkeit bewegt sich die Ringbank mit verschiedener
Geschwindigkeit. Läuft der Faden von der Basis nach der Spitze, so nimmt die
Geschwindigkeit zu, bei umgekehrtem Laufe ab. Die Geschwindigkeiten an gleichen
Punkten der Wege sind bei dem Aufgang und Niedergang in Folge der in den Schichten
liegenden ungleichen Anzahlen von Windungen verschieden; an den Wegenden müssen also
Geschwindigkeitssprünge eintreten, die aber hier auſser Berücksichtigung bleiben
sollen. Ebenso ist nicht berücksichtigt worden, daſs die Ringbank beim Aufgang
gegen, beim Niedergang mit dem Faden läuft.
Um die Untersuchung zum Abschluſs zu bringen, wären endlich noch
die Umdrehungszahlen der Vordercylinder des Streckwerkes zu berechnen.
Läuft der Faden gegen die Kötzerbasis an, so macht der Läufer u1 = 7950 Umdrehungen,
wie oben ermittelt. Haben die Streckcylinder 28mm,575 (1⅛'') Durchmesser, so ist die zu u1 = 7950 gehörige Umdrehungszahl derselben:
m_1=\frac{u_1}{1\,^1/_8\,\pi\,\varphi\,\sqrt{\mbox{Nr.}}}=161.
Auf demselben Wege findet sich die Umdrehungszahl m2 des Streckwerkes,
wenn der Faden gegen die Kötzerspitze läuft:
m_2=\frac{u_2}{1\,^1/_8\,\pi\,\varphi\,\sqrt{\mbox{Nr.}}}=94.
Zusammenstellung der Resultate: Bei dem Spinnen von
Baumwollgarn Nr. 16 eng], auf der Ringbank unter Anwendung eines Läufers von 0g,1 Gewicht und der oben angeführten Gröſsen des
Ringes und Kötzers liegen die Grenzen der Spindelgeschwindigkeit, wenn man den
Coefficienten der Reibung zwischen Läufer und Ring zu 0,1 und die zulässige constant zu haltende Fadenspannung zu 20g annimmt, bei 8020 und 5190 Umdrehungen. Die
Vordercylinder machen bei 1⅛'' engl. Durchmesser dementsprechend 161 und 94
Umdrehungen. Liegen in der von der Spitze nach der Basis gewundenen Schicht 22, in
der von der Basis nach der Spitze gewundenen Schicht 66 Windungen, so ist die Zeit
für einen Niedergang der Ringbank 7,2, für einen Aufgang 2,6 Secunden. – Will man die Fadenspannung constant halten, so muſs während
eines in 7,2 Secunden erfolgenden Niederganges der Ringbank die Spindelumdrehungszahl
von 5190 auf 8020 und die Umdrehungszahl der Streckcylinder von 94 auf 161
anwachsen; während eines in 21,6 Secunden erfolgenden Aufganges nehmen die
Umdrehungszahlen von 8020 auf 5190, bezüglich 161 auf 94 ab.
Es drängt sich sofort die Frage auf, ob wohl dabei die Maschine einen ruhigen Gang
behalten kann? Daran zu zweifeln, ist man voll berechtigt. – Eine geringe Besserung
der Verhältnisse wäre nur dadurch zu erreichen, daſs die Zahl der Windungen in der
fallenden und steigenden Schicht gleich groſs wird. Die Zeit für einen Auf- oder
Niedergang ist dann ½ (7,2 + 21,6) = 14,4 Secunden. Die sehr ungünstigen
Verhältnisse beim Niedergang haben sich gebessert, die beim Aufgang verschlechtert.
Auch erweist sich diese Ausführung in der Praxis als nicht brauchbar.
Die Vaterschaft der Ringbänke mit variabler Spindelgeschwindigkeit behufs Erzielung
constanter Fadenspannung ist meines Wissens Jacob Grime
in Preston zuzuschreiben, welcher die Ausführung der Firma Samuel Brooks in Manchester übertragen hat. Der Textile Manufacturer brachte bereits im Jahrgange 1879 eine kurze
Beschreibung nebst einer völlig ungenügenden Abbildung der Maschine. Unsere
Mülhauser Quelle enthält eine ausführliche Besprechung derselben unter Beigabe sehr
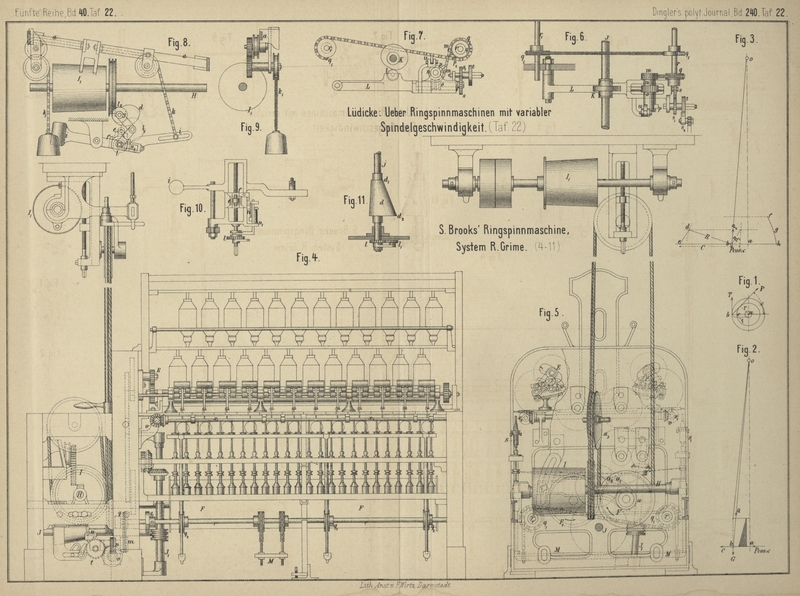
guter Zeichnungen, deren Wiedergabe angeschlossen werden soll. Auf Taf. 22 gibt Fig.
4 eine Längen-, Fig. 5 eine
Stirnansicht der Ringbank. Die Figuren 6
bis 11 enthalten einzelne Mechanismen.
Die Ringbank besitzt, abgesehen von den Theilen, welche die veränderliche
Spindelgeschwindigkeit und Streck Werksgeschwindigkeit veranlassen, im Groſsen und
Ganzen die gewöhnliche Ausführung. Die Maschine ist zweiseitig. Die Streckwerke
liegen etwas geneigt. Nur die Vordercylinder sind mit Lederrollern versehen und
erhalten Druck durch guſseiserne Stäbe D, von denen
jeder quer durch die Maschine geht und für beide Seiten benutzt wird. Mittel- und
Hintercylinder besitzen massive metallene Oberroller ohne besondere
Druckvorrichtungen. Das Rad E ist der Verzugswechsel.
Das Streckwerk wird von der Spindeltrommelwelle durch die Vorgelege
\frac{a}{a_1} \frac{a_2}{a_3} getrieben; das Rad a2 ist hier der
Drahtwechsel. Die Spindeln erhalten Betrieb von der Spindeltrommel F aus. Die Führung der Spindelschnuren ist in folgender
Weise angeordnet. Neben der Trommel F liegt eine zweite
F1 von gleicher
Gröſse, aber ohne besonderen Antrieb. Die von der Spindel S ablaufende Schnur umschlingt einmal die Trommel F, geht nach der Spindel S1, zurück nach F1 umschlingt diese Trommel und läuft nach S. Dadurch liegen die gegen die Spindelwürtel
anlaufenden Schnurentheile fast in gleicher Höhe.
Die Spindeltrommel wird durch ein Doppelseil getrieben. Diese Seile erhalten von der
Antriebwelle H Bewegung. Auf H sitzt ein Riemenkegel I entsprechend zu dem
auf der Deckenvorgelegewelle befindlichen Riemenkegel I1. Der treibende Kegel I1 macht 620
Umdrehungen in der Minute. Sind die Enddurchmesser der Kegel I und I1, 252
bezieh. 230mm und hat die Spindeltrommel F 250mm und der
Spindelwürtel 22mm Durchmesser, so ergeben sich
die Grenzen der Spindelumdrehungen, wenn man vom Gleiten der Riemen und Schnuren
absieht, zu 620\times\,\frac{252}{230}\times\,\frac{250}{22}=7700
bezieh.
620\times\,\frac{230}{252}\times\,\frac{250}{22}=6430.
Die als zur Maschine gehörig bezeichneten Spulen besitzen an tiefster Stelle vor dem
Ansatz ⅝'' und ¼'' engl. Halbmesser, der Ring, wie hiernach anzunehmen, ⅞ Zoll. Um
einen Vergleich der oben ermittelten Spindelumdrehungszahlen mit den früher auf
Grund der aufgestellten Theorie entwickelten Gröſsen zu ermöglichen, wäre nur noch
für den Spulenhalbmesser r = ¼'' engl. die Rechnung
durchzuführen. Man erhält folgendes: Beim Spinnen von Garn Nr. 16 mit der
angegebenen Spindel unter Anwendung eines Läufers von 0g,1 Gewicht und constanter Spannung des Fadens von 20g sind die theoretischen Grenzen der
Spindelumdrehungszahlen 8020 und 5660, die mit der Maschine erreichbaren 7700 und
6430; die Differenz beträgt im ersten Fall 2360, im zweiten Fall 1270. Die Grenzen
sind vom Constructeur der Maschine viel enger gezogen, als die obige Theorie
verlangt. Daraus ist wohl der Schluſs erlaubt, daſs eine constante Fadenspannung
nicht erreicht ist, sondern nur die Grenzen derselben näher an einander gerückt
sind. Der Erbauer ist dazu vielleicht durch die Bedenken, welche einer starken
Variation der Spindel- und Streckwerksgeschwindigkeit entgegenstehen, veranlaſst
worden.
Während des Aufganges der Ringbank ist der Triebriemen von rechts nach links (Fig.
5), während des Niederganges in umgekehrter Richtung zu verschieben. Die
Gröſse dieser Verschiebung ist, vorausgesetzt, daſs auf Papierhülsen oder Holzspulen
ohne Ansatz gesponnen wird, variabel während der Bildung des Ansatzes von
Doppelkegelform, constant während der Bildung des cylindrischen Theiles des
Garnkörpers. Bei Beginn der Ansatzbildung auf den leeren Hülsen ist eine
Verschiedenheit der Durchmesser an der Basis und Spitze nicht vorhanden, die Spindel
rotirt während dieser Zeit mit constanter Geschwindigkeit, der Riemen läuft ganz
links auf den Kegeln Fig. 5. Mit
dem Auflegen jeder neuen Schicht vergröſsert sich der Basisdurchmesser, während der
Durchmesser an der Spitze, wenn man die Spindel als cylindrisch ansieht, constant
bleibt. Mit der Vergröſserung des Basisdurchmessers muſs die Zunahme der
Spindelgeschwindigkeit gleichen Schritt halten. Für jede neue Schicht ist der
Riemen, wenn der Faden gegen die Basis anläuft, etwas weiter nach rechts zu
verschieben. Die gröſste Verschiebung tritt ein, sobald der Basisdurchmesser den gröſsten Werth
erreicht, also die Ansatzbildung vollendet ist. Da nun für jede Ringspindel der
kleinste und der gröſste Kötzerdurchmesser constant sind, so ergibt sich, daſs
derselbe Mechanismus zur Erzielung variabler Spindelgeschwindigkeit für das Spinnen
verschiedener Garnnummern benutzt werden kann. Je gröber das Garn, mit um so weniger
Schichten vollzieht sich die Ansatzbildung, um so stärker ist die Schiebung des
Riemens für jede einzelne Schicht. Damit ist der Einfluſs ausgedrückt, welchen die
Garnnummer auf die Riemenschiebung ausübt.
Die Bewegung der Ringbank und die Riemenverschiebung werden bei der vorliegenden
Maschine von der wagrechten Welle J (Fig. 4 bis
7) abgeleitet, welch letztere von der stehenden Welle J1 aus durch
Schneckengetriebe in langsame Bewegung versetzt wird und zur Hebung und Senkung der
Ringbank eine Curvenscheibe K (Fig. 7)
trägt. K setzt bei der Drehung den Hebel L in eine schwingende Bewegung; in diesem ist vorn eine
kurze Achse gelagert, welche die Kettenscheibe m, das
Schraubenrad n und einen Bund mit der Nase p trägt. Um dieser Welle eine ruckweise Drehung zu
ertheilen, ist die Schnecke o, das Vorgelege s, s1 und das Sperrrad
t angeordnet, in welches sich ein am Gestell
verbolzter Sperrkegel s2 einlegt. Bei jedem Niedergang des Hebels L
erhält somit die Welle r durch die an m und q befestigte Kette
Linksdrehung, r trägt noch mehrere Kettenscheiben q2 (Fig. 4),
deren senkrecht herablaufende Ketten die cylindrischen Trag- und Führungsstangen der
Ringbank tragen. Von der Welle r aus wird aber auch die
Welle r1 (Fig.
6) in Bewegung gesetzt, welche die linksseitige Ringbank führt. Beide
Ringbänke steigen empor, wenn der Hebel L
niederschwingt, und fallen beim Aufgang dieses Hebels. Damit sich die Gleitrolle l des Hebels L jederzeit
sicher an die Curvenscheibe K anlegt, ist an den beiden
Wellen r und r1 noch ein schweres guſseisernes plattenförmiges
Gewicht M (Fig. 4 und
5) angebracht. Bei jedem Niedergang des Hebels L erhält die Kettenscheibe m durch den
beschriebenen Mechanismus eine kleine Drehung und windet etwas Kette auf, wodurch
das allmähliche Ansteigen der Ringbank bewirkt wird. Je nach der Nummer des
gesponnenen Garnes ist die aufzuwindende Kettenlänge zu verändern. Während der
Ansatzbildung muſs die nach je einem Auf- und Niedergang der Ringbank erfolgende
Hebung der letzteren kleiner sein als nach Vollendung des Ansatzes. Dies wird
dadurch erreicht, daſs die Kette m1 während der Ansatzbildung auf einer Nase p2 der Kettenscheibe
q aufruht. Ist ein Abzug vollendet, so hat man die
Ringbänke durch Abwinden der Kette m1 von m aus mit Hilfe
einer auf die Achse t gesteckten Handkurbel zu senken.
Die Endstellung ergibt sich durch das Anlegen der Nase p an den am Hebel L angebrachten Anschlag u.
Die Verschiebung des Betriebsriemens auf den Kegeln I
und I1
behufs Variation der
Spindelgeschwindigkeit ist aus Fig. 8 bis
11 zu ersehen. Die Riemengabel gleitet auf dem Balken a und erhält durch das an die Kette k1, gehängte Gewicht
das Bestreben, nach links zu wandern, wenn es die nach rechts ablaufende und an dem
Hebel i befestigte Kette k
zuläſst. Der Hebel i erhält durch den auf der Welle j festgekeilten Daumen d
eine schwingende Bewegung. Läuft die in einem Support f
des Hebels i gelagerte Rolle e gegen d1
(Fig. 11) an, so ist die Verschiebung des Riemens am kleinsten, die
Ansatzbildung beginnt; läuft sie gegen d2 an, so ist die Verschiebung am gröſsten, die
Ansatzbildung ist vollendet. Die Verschiebung des Schlittens f geschieht durch eine Schaltschraube und die Stirnräder l bis l2. Von der Vollendung des Ansatzes bis zur
Vollendung des Kötzers bleibt die Verschiebung des Betriebsriemens constant, weshalb
der Betrieb der Schaltschraube unterbrochen werden muſs. Das Rad l sitzt mit Nuth und Feder auf der Schaltschraube und
wird durch eine Gabel geführt, welche so lange, als die Gleitrolle e von d1 bis d2 wandert, durch einen kleinen Hebel n gesperrt ist; n wird zu
gehöriger Zeit ausgehoben, die Gabel verschiebt unter Wirkung einer Feder das Rad
l und unterbricht den Eingriff zwischen den
Getrieben l und l1. Nach Vollendung eines Abzuges ist der Schlitten
f in die Anfangsstellung zurückzuführen und der
Eingriff der Räder l und l1 wieder herzustellen.
Schlieſslich sei noch erwähnt, daſs die über den Spindelspitzen befindlichen
Fadenführer so angebracht sind, daſs jeder einzelne aufgeklappt werden kann, aber
auch alle zugleich gehoben werden können, wodurch die Zeit zum Abziehen der vollen
Spulen verkleinert wird. Dem letzteren Zwecke dienen die zwei unterhalb der
Fadenführer liegenden Wellen x1
x2 (Fig. 4 und
5), welche von der quer liegenden und mit einer Handkurbel versehenen
Achse v Drehung erhalten.
Das Bulletin enthält noch weiter die Beschreibung zweier
anderer Anordnungen des Betriebes der Ringbank für Ringspinnmaschinen mit constanter
Spindelgeschwindigkeit, welche etwas wesentlich Neues nicht bieten. Es sei nur
darauf aufmerksam gemacht, daſs in einem Falle versucht worden ist, das
Zurückbringen der Ringbänke in die tiefste Stellung nach Vollendung der Kötzer durch
Maschinenkraft zu vollführen. Ferner ist die Maschine mit selbstthätiger Abstellung
nach Vollendung der Kötzer und mit einer Bremse zum schnellen Anhalten der Spindeln
nach Verlegung des Riemens auf die Losscheibe versehen. Auf den dem Bericht
beigegebenen Tafeln ist eine groſse Zahl von Ringspindeln verzeichnet, welche aber
mit wenigen unwichtigen Ausnahmen in D. p. J. (vgl. Ziffer, Dobson und Macqueen,
Howard und Bullough 1879 231 * 415, Duffiy und Whorwell 1880
236 * 377) bereits beschrieben sind.
Von weit gröſserem Interesse sind die Schluſsbemerkungen des Berichtes über Führung und
Leistung der Ringbänke; diese sind kurz folgende:
Die Führung der Ringbank ist sehr einfach und kann bequem durch junge Arbeiterinnen
besorgt werden, wodurch die Spinnkosten abnehmen. 1 Arbeiterin genügt für 300 bis
400 Spindeln. Das Anknüpfen gebrochener Fäden ist etwas schwieriger als bei dem
Selfactor wegen des rascheren Auf- und Niederganges der Ringbank. Die Arbeiterinnen
werden aber auch darin geschickt. Sie heben entweder die Spule von der Spindel, um
den Faden durch die Läufer ziehen zu können, oder halten die Spindel mit dem Knie in
Ruhe und haben dann beide Hände zum Anknüpfen des Fadens frei, weil die Spule nicht
abgehoben wird.
Bei einigen Ringspindeln muſs man, nachdem die Kötzer vollendet sind, die Ringbank
bis zur tiefsten Stelle senken und noch eine kleine Länge Garn auflaufen lassen, um
den Faden an der Spindel zu befestigen und nach dem Aufstecken leerer Spulen das
Spinnen sogleich wieder beginnen zu können. Dank dieser Vervollkommnungen können 4
geübte Arbeiter den Abzug bei einer Maschine von 360 Spindeln in 2,5 bis 3 Minuten
bewerkstelligen. Um diesen Stillstand noch mehr zu verringern – was beim Spinnen
niederer und mittlerer Nummern, wobei die Abzüge sehr rasch auf einander folgen, von
Wichtigkeit ist –, hat man einen Apparat angebracht, durch welchen das Abheben aller
gefüllten Spulen mit einem Male geschieht. Das Anlassen der Ringbank erfolgt dann
bereits wieder nach 30 Secunden. Leider ist der Apparat bisher nur anwendbar, wenn
auf Holzspulen gewickelt wird.
Die Ringbank ist unzweifelhaft eine weit einfachere Maschine als der Selfactor,
erfordert weniger Sorgfalt und Geschicklichkeit für gute Instandhaltung und weniger
Anstrengung seitens der Arbeiter. Am Selfactor muſs ein kräftiger Mann angestellt
werden, die Ringbank können junge Burschen oder Mädchen bedienen.
Das auf Ringbänken gesponnene Garn wird als besser bezeichnet wie das vom Selfactor
gelieferte und als Grund dafür der ununterbrochene Gang (?) angegeben. Ringbankgarn
soll viel regelmäſsiger sein und weniger Fehler zeigen als Selfactorgarn. Der
Raumbedarf ist für Ringspindeln bedeutend geringer. Man kann im gleichen Räume 50
Procent mehr Ringspindeln als Selfactorspindeln aufstellen. Der Kraftbedarf soll
sich für gleiche Leistung ziemlich gleich stellen. Die Ringspindeln sind meist so
construirt, daſs die Lager thunlichst von Staub und Fäserchen geschützt sind und das
Schmieren nur in längeren Zeiträumen zu erfolgen braucht. Die Selfactorspindeln
müssen im Tage mindestens 2 mal geölt werden.
Bezüglich der Leistungsfähigkeit scheinen die von verschiedenen Constructeuren und
Spinnern veröffentlichten Angaben nicht übertrieben. In der Mülhauser Schule für
Spinnereitechniker hat man auf Grund von Versuchen die mögliche Leistung
folgendermaſsen gefunden: Bei Kette Nr. 27/29 mit 10 Drehungen auf 1cm, 6500 Umdrehungen der Spindel im Mittel, 90
Umdrehungen der vorderen Streckcylinder 100g für
Spindel und Tag, bei Kette Nr. 40/42 dagegen 60g
in 12 Stunden. Die Läufer sind bei 6000 bis 8000 Spindelumdrehungen sehr rasch der
Zerstörung unterworfen; trotzdem betragen die Kosten dafür nur etwa 17,50 Mark für
1000 Spindeln und Jahr. Die Läufer werden mit Nummern bezeichnet meist in der Weise,
daſs Nr. 15 dem schwersten Läufer für das gröbste Garn zuertheilt wird. Die Nummern
gehen immer um 1 herunter bis Nr. 1 und steigen dann wieder auf, erhalten aber zum
Unterschied einen Bruchstrich mit Null darunter; Nr. 15/0 bezeichnet den leichtesten Läufer für das feinste Garn. Für gleiche
Garnnummern müssen je nach Spindelgeschwindigkeit und Ringdurchmesser Läufer
verschiedenen Gewichtes angewendet werden, wie dies auch aus der eingangs gegebenen
theoretischen Untersuchung hervorgeht.
A. Lüdicke.
Tafeln