| Titel: | Zur Untersuchung der atmosphärischen Luft. |
| Fundstelle: | Band 240, Jahrgang 1881, S. 447 |
| Download: | XML |
Zur Untersuchung der atmosphärischen
Luft.
Mit Abbildungen auf Tafel 36.
Zur Untersuchung der atmosphärischen Luft.
Im Anschluſs an die früheren Mittheilungen (1879 234 * 46. 1880 236 * 66) mögen
zunächst die neueren Apparate zur Bestimmung der
Luftfeuchtigkeit besprochen werden.
A. Voller (Verhandlungen des
Naturwissenschaftlichen Vereines von Hamburg, Sonderabdruck) verwendet
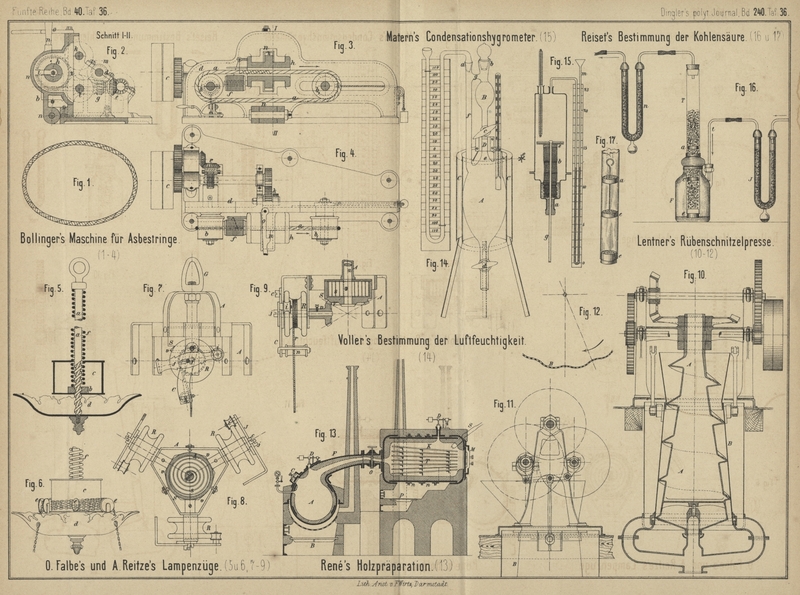
einen länglich eiförmigen Gasbehälter A (Fig.
14 Taf. 36) von etwa 150cc Inhalt,
dessen Erweiterung des Halses B von etwa 8 bis 10cc zur Aufnahme der Schwefelsäure dient, welche
durch die Oeffnung b eingefüllt wird, beim Oeffnen des
Hahnes c an der inneren Wandung von A herabflieſst und später durch Hahn d abgelassen werden kann. Um eine weite Ausbreitung der
Schwefelsäure auf der Glaswand zu erreichen, ist unterhalb c in den kreisförmigen Querschnitt des Glashalses ein aus Glasstäbchen
gebildeter Stern e eingeschmolzen; indem die
Schwefelsäure durch dessen Zwischenräume hindurchflieſst, vertheilt sie sich und
breitet sich allerseits auf der inneren Glaswandung aus. Eine Glasröhre f steht durch die Querröhre g mit dem oberen Theile des Glasgefäſses in Verbindung und dient dazu, der
durch die herabflieſsende Schwefelsäure verdrängten Luft Abfluſs zu gestatten, ohne
sie aus dem Gefäſse zu entfernen. Der obere Theil dieser Röhre bei a dient gleichzeitig zum Aufsetzen des mit einer
Millimeterscale versehenen Manometers. Ein Thermometer ist in das Gefäſs A eingeschmolzen oder auch, behufs etwaiger Fortnahme
desselben, nur ein geschliffen und verkittet.
Als Manometerflüssigkeit kann bei starken Feuchtigkeitsmengen, also groſser Druck
Verminderung, Quecksilber in einer kurzen Manometerröhre dienen. Zweckmäſsiger
jedoch ist es, um feinere Spannungsunterschiede sichtbar zu machen, eine leichtere
Flüssigkeit in einer längeren Röhre anzuwenden. So lange die Temperatur nicht unter
den Gefrierpunkt sinkt, kann man gefärbtes Wasser anwenden, da die Befürchtung, es
möchten die durch das enge Manometerrohr in das Gefäſs A etwa entweichenden Dämpfe dieses Wassers einen störenden Einfluſs
ausüben, sich nicht bestätigt hat. Behufs Abhaltung äuſserer Wärmestrahlen ist das
Instrument von einem doppelten Messingmantel C so
umschlossen, daſs die Hähne c und d bequem erreichbar sind. Der Mantel dient mit Hilfe
der Klemme D zugleich als Träger.
Nachdem der Stöpsel b, sowie die Hähne c und d geöffnet worden,
wird mittels eines an der Ausfluſsöffnung angelegten Schlauches kurze Zeit die
äuſsere Luft durch den Apparat hindurchgesaugt. Hierauf wird der Hahn c geschlossen, B bis
unterhalb g mit concentrirter Schwefelsäure gefüllt und
dann der Stöpsel b eingesetzt. Nachdem die Temperatur
t des Apparates constant geworden, wird diese,
sowie der herrschende Barometerstand notirt, der Hahn d
geschlossen und c geöffnet. Die Schwefelsäure flieſst
langsam an der inneren Wandung herab und sammelt sich über d; die verdrängte Luft geht nach B, so daſs
die eingeschlossene Luftmenge unverändert bleibt. Sofort beginnt die Absorption und
ist schon nach wenigen Minuten fast vollständig beendet; die Manometerflüssigkeit
steigt in dem inneren Schenkel rasch empor und erlangt bald einen festen Stand. In
Folge der Condensationswärme des Wasserdampfes und etwa nicht völlig vermiedener
äusserer Bestrahlung findet während dessen gewöhnlich eine Temperaturerhöhung ϑ
statt, welche jedoch in der Regel nur zwischen 0,1 und 0,40 beträgt.
Die Spannung e des Wasserdampfes der
in dem Hygrometer eingeschlossenen Luft kann in folgender Weise abgeleitet werden.
Die Manometerflüssigkeit sei Quecksilber, ferner sei q
der Querschnitt der Manometerröhre in Quadratmillimeter; 7 das Gesammtvolumen des
Hygrometers bis zum Nullpunkt des Manometers, jedoch abzüglich des von der
Schwefelsäure erfüllten Raumes B: V sei ausgedrückt
durch Einheiten, deren eine das Volumen von 1mm
Länge der Manometerröhre bildet, so dass q × V
Cubikmillimeter den Inhalt des Apparates darstellen, b
sei der herrschende Barometerstand, e die wahre
Dampfspannung bei der Beobachtungstemperatur t in
Millimeter Quecksilber e die beobachtete
Manometerdifferenz bei der Temperatur t1 = t + ϑ.
Bei einem Apparat ergab sich z.B. mittels Quecksilberkalibrirung
q = 4qmm,971 und
V = 31905. Die Spannung der im Volumen V eingeschlossenen Luft bei der Temperatur t ist vor der Absorption gleich b, nach der Absorption gleich b – e;
beobachtet wird b – ε bei
der Temperatur t1 im
Volumen V = ½ ε.
Mithin ist:
b-e=\frac{(b-\varepsilon)\,(V-1/2\,\varepsilon)\,(1+\alpha\,t)}{V\,(1+\alpha\,t_1)},
wo α der
Ausdehnungscoefficient der Luft = 1/273 oder, da t1 = t + ϑ,
b-e=\frac{(b-\varepsilon)\,(V-1/2\,\varepsilon)\,(273+t)}{V\,(273+t+\vartheta)},
woraus
e=\frac{b\,\vartheta}{273+t+\vartheta}+\varepsilon\,\frac{273+t}{273+t+\vartheta}+\varepsilon\,\frac{(b-\varepsilon)\,(273+t)}{2\,V\,(273+t+\vartheta)}
Durch Addition und Subtraction von \varepsilon\,
\frac{\vartheta}{273+t+\vartheta} erlangt dieser Ausdruck die Form:
e=\varepsilon\,\left[1+\frac{(b-\varepsilon)\,(273+t)}{2\,V\,(273+t+\vartheta)}\right]+\frac{b-\varepsilon}{273+t+\vartheta}\,\vartheta.
Da ϑ immer sehr klein ist, so kann der Factor
\frac{273+t}{273+t+\vartheta} des ohnehin kleinen Gliedes
\frac{b-e}{2\,V} ohne Fehler gleich 1 gesetzt werden, so daſs
die allgemeine Formel für das Absorptionshygrometer bei Anwendung von Quecksilber
als Manometerflüssigkeit lautet:
e=\varepsilon\,\left(1+\frac{b-\varepsilon}{2\,V}\right)+\frac{b-\varepsilon}{273+t_1}\,\vartheta,
. . . . . . (1)
wo das zweite Glied die Temperaturcorrection
enthält.
Um für mittlere Barometerstände der Berücksichtigung des
herrschenden Luftdruckes enthoben zu sein, kann man in folgender Weise verfahren.
Setzt man b = 760 + m (wo
m positiv oder negativ sein kann), so erhält
man:
e=\varepsilon\,\left(1+\frac{760}{2\,V}\right)+\frac{760}{273+t_1}\,\vartheta+(m-\varepsilon)\,\left(\frac{\varepsilon}{2\,V}+\frac{\vartheta}{273+t_1}\right)
. . . . . . . (2)
Der Factor von s im ersten
Gliede dieser Formel wird für jedes Instrument constant und heiſse A: bei dem oben erwähnten z.B.
A=1+\frac{760}{63810}=1,012.
So lange ϑ klein bleibt, wird auch
der Werth des Factors \frac{760}{273+t_1} bezieh. des zweiten
Gliedes der Formel (2) selbst bei verschiedenen Beobachtungstemperaturen nur sehr
wenig von demjenigen Betrage abweichen, den derselbe bei einer mittleren
Lufttemperatur erlangt, so daſs die durch den Factor des zweiten Gliedes der Formel
(2) ausgedrückte Temperaturcorrection für mittlere Verhältnisse ebenfalls die Form
einer Constanten annimmt.
Für Beobachtungstemperaturen von 10 bis 30° erlangt dieselbe den
Werth 2,60 oder
0,260 für jedes Zehntel eines Grades der beobachteten Temperaturdifferenz ϑ. Demnach haben wir als brauchbare
Annäherungsformel:
e=A\,\varepsilon+B\,\vartheta+C, . . .
. . . . . (3)
wo
A=1+\frac{760}{2\,V},\ B=2,60,\
C=(m-\varepsilon)\,\left(\frac{\varepsilon}{2\,V}+\frac{\vartheta}{273+t_1}\right).
In der Regel wird man übrigens innerhalb der Grenzen der
Beobachtungsfehler bleiben, wenn man im 2. Gliede dieser Formel jedes Zehntel von
ϑ mit 0,25 multiplicirt, was für die Rechnung
bequemer ist. Das Glied
C=(m-\varepsilon)\,\left(\frac{\varepsilon}{2\,V}+\frac{\vartheta}{273+t_1}\right)
der Formel (3) besteht aus zwei Factoren, von denen der eine
\left(\frac{\varepsilon}{2\,V}+\frac{\vartheta}{273+t_1}}\right)
stets klein bleibt, während der andere (m – ε) bei extremen Barometerständen einen beträchtlichen
Werth erreichen kann.
Innerhalb des Temperaturunterschiedes von – 20 bis + 40° kann ε im Falle der Sättigung von 1 bis 50mm wechseln, so daſs bei einem mittleren Werth von
V = 30000 das Glied
\frac{\varepsilon}{2\,V} zwischen 1/60000 und 1/1200 betragen
kann; bei + 20° und gesättigter Atmosphäre erlangt es beispielweise den Werth 1/3600. Das Glied
\frac{\vartheta}{273+t_1} wird meist = 0 oder doch so klein
sein, daſs der ganze Factor in der Regel den Werth 0,001 nicht erreichen wird.
Daraus folgt, daſs C unberücksichtigt bleiben kann, so
lange m – ε nicht groſs wird. In der Regel wird bei
Anwendung von Quecksilber als Manometerflüssigkeit das Glied C ganz unberücksichtigt bleiben können, so daſs dann die Hygrometerformel
die einfache Gestalt annimmt:
e=A\,\varepsilon+B\,\vartheta, . . . .
. . . . (4)
worin A=1+\frac{760}{2\,V} und
B=2,60. Für obiges Instrument ist dann
e=1,012\varepsilon+2,6\vartheta.
Wendet man, behufs Verkleinerung der Beobachtungsfehler, eine
Manometerflüssigkeit von geringerem specifischem Gewichte d (Quecksilber – D) an, so wird, wenn ε1 die beobachtete
Manometerdifferenz bedeutet:
e=\varepsilon_1\,\left(\frac{d}{D}+\frac{b-\varepsilon_1\,\frac{d}{D}}{2\,V}\right)+\frac{b-\varepsilon_1\,\frac{d}{D}}{273+t_1}\,\vartheta.
Dies ist somit die allgemeine Formel für die atmosphärische
Dampfspannung bei beliebiger Manometerflüssigkeit. In gleicher Weise ergeben sich
für mittlere Barometer- und Thermometerstände die Annäherungsformeln:
e=\varepsilon_1\,\left(\frac{d}{D}+\frac{760}{2\,V}\right)+\frac{760}{273+t_1}\,\vartheta+\left(m-\varepsilon_1\,\frac{d}{D}\right)\
\left(\frac{\varepsilon_1}{2\,V}+\frac{\vartheta}{273+t_1}\right)
und
e=A_1\,\varepsilon_1+B\,\vartheta+C_1,
wo
A_1=\left(\frac{d}{D}+\frac{760}{2\,V}\right),\ B=2,60,\
C_1=\left(m-\varepsilon_1\,\frac{d}{D}\right)\
\left(\frac{\varepsilon_1}{2\,V}+\frac{\vartheta}{273+t_1}\right).
Bei der letzten Formel ist zu beachten, daſs in dem Glied C1 der Quotient
\frac{\varepsilon_1}{2\,V} einen im Verhältniſs von d : D gröſseren Werth besitzt als der entsprechende
\frac{\varepsilon}{2\,V} bei Formel (3), während der Factor
\left(m-\varepsilon_1\,\frac{d}{D}\right) denselben Werth wie
(m – e) behält. Daraus
folgt, daſs die Grenzen, innerhalb deren C1 vernachlässigt werden kann, entsprechend enger
werden; nichts desto weniger liegt die durch C1 ausgedrückte Correction für gewöhnliche
Verhältnisse noch völlig innerhalb der Grenzen der Beobachtungsfehler.
Benutzt man Wasser als Manometerflüssigkeit, so wird
\frac{d}{D}=0,074. Die letzte Formel erhielt demgemäſs für
oben erwähntes Instrument die Gestalt:
e=0,086\,\varepsilon_1+2,60\,\vartheta+(m-0,074\varepsilon_1)\
\left(\frac{\varepsilon_1}{63810}+\frac{\vartheta}{273+t_1}\right),
wovon
e=0,086\,\varepsilon_1+2,60\,\vartheta zur Berechnung der
Beobachtungen benutzt wurde.
F. Neesen (Annalen der
Physik, 1880 Bd. 11 S. 526) hat das Hygrometer von Rüdorff (1880 236 * 67) dahin geändert, daſs er zwei Flaschen verwendet,
welche mit einander verbunden sind und dadurch die Beobachtung von der Temperatur
unabhängig zu machen.
A. Matern (Daselbst, Bd. 10 S. 149) hat sein Condensationshygrometer (1880 236 68) jetzt dahin
geändert, daſs der Glasboden unten in einen 1cm,5
langen, 1cm weiten Hals a (Fig. 15
Taf. 36) endet, welcher zur Aufnahme eines Kautschukcylinders bestimmt ist. Vom
oberen Ende des Halses an erweitert sich der Boden in einem 3cm weiten und 3cm hohen cylindrischen Raum, der zur Füllung mit Wasser dient. Die Wand
dieses Behälters geht in einen möglichst geebneten, horizontal abstehenden Rand von
1cm Breite über, erhöht sich dann noch etwa um
1cm, bei welcher Stelle eine Weite von 5cm erreicht ist, und läuft dann in einen
rechtwinklig abstehenden flachen Rand von 1cm
Breite aus, der mit Schmirgel sorgfältig eben geschliffen ist. In einer Durchbohrung
des Kautschukpfropfens läſst sich ein 2mm,5
starker Glasstab g mit Reibung auf- und abschieben, auf
welchen zunächst ein mitten durchbohrtes Metallkreuz von 2cm Armlänge und darunter eine ebene, leicht
biegsame Kautschukscheibe von 4cm Durchmesser
geschoben ist. Beide Theile werden durch einen mit starker Reibung auf den Stab
geschobenen kurzen Kautschukcylinder e von 2cm Durchmesser festgehalten, an welchem ein den
Stab umgebendes, etwa 15cm langes Säckchen b von dünner Leinwand befestigt ist. In den geöffneten
Behälter ist bis zu einer Marke so viel Wasser zu gieſsen, daſs es nach dem
Herabziehen des Stabes durch die eingetauchte Leinwand und den Kautschukcylinder
noch nicht bis an den Rand des Behälters gehoben wird. Wenn das Kreuz die
Kautschukscheibe gegen diesen Rand andrückt, ist der Wasserbehälter genügend
geschlossen, um den Feuchtigkeitsgehalt der auſserhalb befindlichen Luft unverändert
zu lassen. Der eben geschliffene Rand des Bodens wird dann mit Talg bestrichen und
ein mit gleichem Rande versehener 12cm hoher, 5cm weiter Behälter fest darauf gedrückt, in
welchen oben ein 2mm,75 bis 3mm weites und 30cm langes, zur Hälfte mit Rüböl gefülltes Manometer m entweder eingeschmolzen, oder in einen Hohlconus
eingesetzt ist. Der Stab ist dann in die Höhe zu schieben und die mit ihm
emporgehobene feuchte Leinwand sättigt die Luft sehr bald mit Wasserdampf, dessen
Druckerhöhung sich am Manometer zeigt.
Zur Bestimmung der Kohlensäure soll
man nach J. Reiset (Comptes
rendus, 1880 Bd. 90 S. 1144) eine gröſsere Menge Luft verwenden, als dies
bis jetzt meist geschehen ist. Die angesaugte Luft tritt zunächst in ein U-förmiges, mit durch
concentrirte Schwefelsäure befeuchteten Bimssteinstücken gefülltes Rohr J (Fig. 16
Taf. 36), um ihren Wassergehalt an diese abzugeben, während die gebildete verdünnte
Säure sich in der unten angeschmolzenen Kugel sammelt. Die trockene Luft tritt nun
durch das Rohr t in das Absorptionsgefäſs F, in dessem Halse ein 0m,5 langer Glascylinder T mittels Gummikappe
befestigt ist. In diesen Cylinder sind 3 siebartig durchlöcherte Platinkapseln a, c und e (Fig.
17) von 4cm Durchmesser eingeschoben.
Man bringt in denselben 300cc Barytwasser und
verbindet ihn mit dem Trockenrohr n. In Folge der
feinen Vertheilung der durchgesaugten Luft durch die Platinsiebe wird die
Kohlensäure völlig von dem Barytwasser zurückgehalten. Sind etwa 600l Luft hindurchgesaugt, so bestimmt man unter
Berücksichtigung des verdunsteten und vom Rohre n
aufgenommenen Wassers durch Titration die Menge des ausgefällten Baryts.
Nach Kapusstin (Berichte der deutschen chemischen Gesellschaft, 1880 S.
2376) kann man den Kohlensäuregehalt der Luft dadurch bestimmen, daſs man
Natriumhydrat in 90procentigem Alkohol löst, die Lösung mit Luft schüttelt und
hernach so viel Wasser hinzusetzt, als zur Auflösung des Carbonates erforderlich
erscheint. Nach seinen Untersuchungen ergibt sich, daſs, wenn man zur Auflösung des
Carbonates n Cubikcentimeter Wasser (von gewöhnlicher
Temperatur) verwendet hat, sich die Anzahl der Cubikcentimeter Kohlensäure (x) bei 760mm und 0°
aus der Gleichung berechnen läſst: x=\frac{n-6,5}{0,55}.
Der Versuch wird in folgender Weise ausgeführt: Um den Kohlensäuregehalt der in einer
Flasche von 5l enthaltenen Luft zu bestimmen, gibt
man in die Flasche 75cc weingeistige Natronlauge
(1l der Lösung enthält 0g,5 NaOH), schüttelt alsdann ½ Stunde lang, gieſst
die Flüssigkeit aus, nimmt von derselben unter Umrühren 25cc, setzt zu derselben aus einer Bürette nach und
nach Wasser bis zum Verschwinden der Trübung hinzu und multiplicirt das nach der
Formel berechnete Resultat mit 3. – Das Verfahren verspricht wenig genaue
Resultate.
Der Kohlensäuregehalt der atmosphärischen
Luft betrug nach Versuchen von G. F. Armstrong
(Proceedings of the Royal Society, 1880 Bd. 30 S.
343) zu Grasmere in Westmoreland im Durchschnitt des Mittags 2,9603 und des Nachts
3,2999 Vol. auf 10000. – Nach A. Levy (Comptes rendus, 1880 Bd. 90 S. 32) schwankte der
Kohlensäuregehalt der Luft in Montsouris zwischen 2,2 bis 3,6 Vol. Marié-Davy (Daselbst, S. 1287) glaubt diese
Schwankungen auf den Einfluſs der Windrichtung zurückführen zu können. J. Reiset (Daselbst, 1879 Bd. 88 S. 1007. 1880 Bd. 90
S. 1144 und 1457) schlieſst jedoch aus seinen Versuchen, daſs derartige Schwankungen
lediglich auf die Ungenauigkeit der Untersuchungsmethode zurückzuführen sind und
thatsächlich nicht vorkommen. Er fand in Dieppe im Durchschnitt 2,942 Vol. mit
Schwankungen von höchstens 0,3. Der Kohlensäuregehalt der Luft im Walde und auf
Kleefeldern war fast genau so hoch als auf der Untersuchungsstation, so daſs also
die Kohlensäure sehr rasch sich in der Luft vertheilt. Die Luft in Paris enthielt
3,027 Vol. Eine andere Versuchsreihe gab auf der Versuchsstation am Tage 2,891, in
der Nacht 3,084 Vol. bei einem Gesammtdurchschnitt von 2,978. Bei einem sehr starken
Nebel stieg jedoch der Kohlensäuregehalt sogar auf 3,415 Vol. Th. Schlösing (Comptes
rendus, 1880 Bd. 90 S. 1410) erklärt den gleichmäſsigen Kohlensäuregehalt
der Atmosphäre durch die ausgleichende Wirkung des Meeres.
H. Macagno (Chemical News,
1880 Bd. 41 S. 97) hat auf der Versuchsstation in Palermo i. J. 1879 eine Reihe von
Luftanalysen ausgeführt. Der Sauerstoff wurde mit
pyrogallussaurem Kalium, die Kohlensäure gewichtsanalytisch mit Kalilauge bestimmt.
Ferner wurde Luft durch Wasser gesaugt und dieses auf Ammoniak mit dem Neſsler'schen
Reagens, auf Nitrate mit Indigo und auf organische Stoffe mit übermangansaurem
Kalium geprüft. Folgende Tabelle zeigt die Bestandtheile von 100l Luft:
Datum
Sauerstoff
Kohlensäure
Salpetersäure
Ammoniak
Organisch
Für 10 Tage
MittlereTemperatur
Regenfall
l
l
mg
mg
Grad
mm
Februar 10
–
–
–
–
–
12,4
11,58
„ 20
20,879
0,021
–
0,024
0,154
13,6
17,29
„ 28
20,891
0,048
–
0,028
0,127
12,8
3,57
März 10
20,715
0,025
–
–
0,115
9,8
9,24
„ 20
19,994
0,025
–
–
0,094
13,3
–
„ 31
20,888
0,022
–
–
0,070
14,4
30,61
April 10
20,910
0,021
–
Spur
0,076
14,3
32,01
„ 20
20,880
0,064
–
–
0,094
15,8
18,45
„ 30
20,898
0,045
–
–
0,055
16,0
14,75
Mai 10
20,913
0,005
–
–
0,020
14,6
17,20
„ 20
20,902
0,049
–
–
0,072
14,0
16,65
„ 31
20,017
0,033
–
0,036
0,142
19,8
2,23
Juni 10
20,894
0,041
–
–
0,107
20,5
–
„ 20
20,918
0,043
–
0,040
0,363
22,0
„ 30
20,915
0,043
–
0,009
0,162
23,5
–
Juli 10
20,977
0,020
Spur
0,010
0,111
23,4
„ 20
20,984
0,076
–
0,080
0,157
22,6
„ 31
20,899
0,039
–
–
0,138
23,0
–
August 10
20,910
0,028
Spur
0,005
0,165
25,1
„ 20
20,888
0,030
–
0,007
0,112
25,1
–
„ 31
20,895
0,039
–
0,009
0,131
25,0
–
Mittel I
20,717
0,033
0
0,008
0,102
14,2
173,18
Mittel II
20,920
0,039
Spur
0,009
0,160
23,4
0
Das erste Mittel gilt für die Monate Februar, März, April und Mai, mit Regen, das
zweite für Juni, Juli und August, ohne Regen. Demnach ist die Luft nach dem Regen
reiner als vorher. Bemerkenswerth ist noch der geringe Sauerstoffgehalt der Luft, wenn der
Sirocco aus Afrika bläst, wie folgende Analysen zeigen:
1879 März 20
19,994 Proc. Sauerstoff
„ 21
20,008
„ 22
20,064
April 15
19,998
Mai 29
20,021
„ 30
20,032
„ 31
20,017
A. Levy (Comptes rendus,
1880 Bd. 91 S. 94) fand auf der Versuchsstation Montsouris in 100cbm Luft im Januar 1879 1mg,9 Ammoniakstickstoff, im Februar 2mg,0, März 1mg,9, April 2mg,2 und im Mai 2mg,1 Ammoniakstickstoff (14 Stickstoff = 17
Ammoniak). Ferner in:
Juni
Juli
Aug.
Sept.
Oct.
Nov.
Dec.
Montsouris
2,1
2,1
2,3
2,4
2,2
1,9
1,7mg
Père-Lachaise (Kapelle)
2,2
2,2
2,3
–
2,1
2,6
–
Père-Lachaise (Nord)
1,9
2,3
2,5
2,1
2,2
2,8
–
Gennevilliers
2,2
3,7
3,7
3,7
4,6
3,7
–
Clichy
1,8
1,7
1,7
1,9
1,9
2,7
–
Pariser Kanäle
–
4,9
–
4,6
–
8,0
9,4
Als Jahresdurchschnitt ergab sich ein Gehalt an
Ammoniakstickstoff für 100cbm Luft i. J. 1877 von
3mg, i. J. 1878 von 2,3 und i. J. 1879 von
1mg,9.
Zur Bestimmung des organischen
Kohlenstoffes in der Luft saugen Dupre und Hake (Chemical News, 1881
Bd. 43 S. 69) dieselbe durch Barytwasser, um den Kohlensäuregehalt festzustellen,
sodann eine gleiche Luftmenge nach der Filtration durch Asbest über glühendes
Kupferoxyd und dann durch den Absorptionsapparat. Der Unterschied der beiden
Kohlensäurebestimmungen wird auf organischen Kohlenstoff berechnet. 10l Luft enthielten danach 0,1 bis 0mg,2 organischen Kohlenstoff. – Den doch
wahrscheinlich vorhandenen Kohlenoxydgehalt der Londoner Luft haben die Verfasser
nicht berücksichtigt (vgl. F. Fischer 1880 235
440).
Tafeln