| Titel: | W. D. Marks' Construction des Fehlergliedes im Zeuner'schen Schieberdiagramm; von Ingenieur Müller-Melchiors. |
| Autor: | Müller-Melchiors |
| Fundstelle: | Band 241, Jahrgang 1881, S. 161 |
| Download: | XML |
W. D. Marks' Construction des Fehlergliedes im
Zeuner'schen Schieberdiagramm; von Ingenieur Müller-Melchiors.
Mit Abbildungen auf Tafel 13.
Müller-Melchiors, über Marks' Construction des
Fehlergliedes.
Der wahre Abstand des Schiebermittels vom Achsmittel bei der einfachen
Schiebersteuerung ist nach Zeuner:
s=r\,sin\,(\omega+\delta)+l\,\sqrt{1-\left(\frac{r}{l}\right)^2\,cos^2\,(\omega+\delta)}
mit den bekannten Bezeichnungen von r,
l, δ und ω für den Radius des Excenterkreises,
die Excenterstangenlänge, den constanten Voreilwinkel und den variablen
Kurbelwinkel; die Schieberstangenlänge ist dabei gleich Null gesetzt. Nach einer
unter allen Umständen erlaubten Reduction ergibt sich:
s=r\,sin\,(\omega+\delta)+l-\frac{r^2}{2\,l}\,cos^2\,(\omega+\delta)
und der Ausschlag des Schiebers aus seiner wirklichen
Mittelstellung ist:
\xi=r\,sin\,(\omega+\delta)-\frac{r^2}{2\,l}\,cos^2\,(\omega+\delta).
Für unendlich lange Excenterstangen wird
\xi=r\,sin\,(\omega+\delta) und man begeht, denselben Werth
auch für endliche Excenterstangenlängen beibehaltend, einen Fehler vom Betrag
z'=\frac{r^2}{2\,l}\,cos\,(\omega+\delta). Dieser Ausdruck
nimmt für \omega=0 und \omega=180
entgegengesetzt bezeichnete Werthe an, bedingt somit ungleiches lineares Voreilen,
verschwindet nur bei den äuſsersten Schieberstellungen, erreicht sein Maximum in der
Nähe des Dampfabschlusses und beeinträchtigt so die Anwendung des Diagrammes auf
praktische Fälle in hohem Grade.
Darum stellte Zeuner die früher auch von den Praktikern
allgemein anerkannte Bedingung auf, das lineare Voreilen solle beiderseits gleich,
d.h. das Fehlerglied solle in den todten Punkten gleich Null werden; gleichzeitig
damit wurde als der wahre Schwingungsmittelpunkt des Schiebers nicht der zwischen
den äuſsersten Ausschlägen in der Mitte liegende Punkt, sondern die Halbirung der
Todtpunktstellungen erklärt und der Schieberausschlag aus diesem Punkte mit ξ
bezeichnet. Dieser
Schwingungsmittelpunkt steht nun nicht mehr um den Betrag l vom Achsmittel ab, sondern um den Werth:
d=\frac{s\,(o^\circ)+s\,(180^\circ)}{2}=l-\frac{r^2}{2\,l}\,cos^2\,\delta
und der Schieberausschlag wird:
\xi=s-d=r\,sin\,(\omega+\delta)+\frac{r^2}{2\,l}\,[cos^2\,\delta-cos^2\,(\omega+\delta)].
Das Fehlerglied
z=\frac{r^2}{2\,l}\,[cos^2\,\delta-cos^2\,(\omega+\delta)]
wird gleich Null für \omega=0,\ 180,\ 180-2\,\delta,\
360-2\,\delta und erreicht sein Maximum für
\omega=90-\delta,\ 270-\delta positiv, für
\omega=180-\delta und 360-\delta
negativ.
Hier wird also thatsächlich der störende Einfluſs des Fehlergliedes auf ein Minimum
reducirt und war sonach Zeuner gewiſs berechtigt, die
Berücksichtigung des Fehlergliedes im Diagramm gar nicht zu versuchen. Einen
praktischen Werth hat ein näheres Eingehen unter gar keinen Umständen, nachdem das
einfache Diagramm es ermöglicht, alle Hauptmaſse in wenig Minuten festzustellen, das
Ausmitteln aber, wie durch kleine Aenderungen und Verschiebungen die unvermeidlichen
Fehler, welche vor Allem aus der endlichen Treibstangenlänge entstehen, thunlichst
zu vermindern wären, doch nur an einem Modell oder an der fertigen Maschine
stattfinden kann. In noch höherem Grade eilt dies selbstverständlich bei
Coulissensteuerungen, wo auch die genaueste Darstellung jedes einzelnen Fehlers ganz
werthlos ist, so lange es nicht gelingt, den combinirten Einfluſs sämmtlicher
Fehlerquellen – und wie viele bleiben hier noch selbst bei günstigen
Stangenverhältnissen bestehen – zu charakterisiren.
Dies muſste vorausgeschickt werden, um den richtigen Standpunkt zur Betrachtung der
Diagrammconstruction von Prof. William D. Marks in
Philadelphia einzunehmen. Dieselbe ist von überraschender Einfachheit und basirt auf
einer höchst originellen Entwicklung, kann jedoch nur wesentlich theoretisches
Interesse erwecken und wird sich nie einen Weg in die Praxis bahnen.
Zur graphischen Darstellung des Fehlergliedes wandelt Marks dasselbe in eine Function des theoretischen Schieberausschlages ξ um und transformirt zunächst in dem oben entwickelten
Werth von z das zweite Glied
cos^2\,(\omega+\delta) in
1-sin^2\,(\omega+\delta); demnach ergibt sich:
2\,l\,z=r^2\,cos^2\,\delta-r^2+r^2\,sin^2\,(\omega+\delta)=r^2\,cos^2\,\delta-r^2+\xi^2
und endlich
\xi^2=2\,l\,z+C, wobei
C=r^2\,(1–cos^2\,\delta).
Dies ist die Gleichung einer Parabel, deren Scheitel um
\frac{r^2\,(1-cos^2\,\delta)}{2\,l} hinter der Ordinatenachse
liegt, deren Ordinaten die theoretischen Schieberausschläge sind, die Abscissen
dagegen die den betreffenden Werthen von ξ
entsprechenden Werthe des Fehlergliedes, positiv oder negativ, je nachdem sie vor
oder hinter der Ordinatenachse liegen.
Da von der Parabel nur die nächst dem Scheitel liegenden Strecken benutzt werden,
genügt die Einsetzung des im Scheitel osculirenden Kreises mit dem halben Parameter
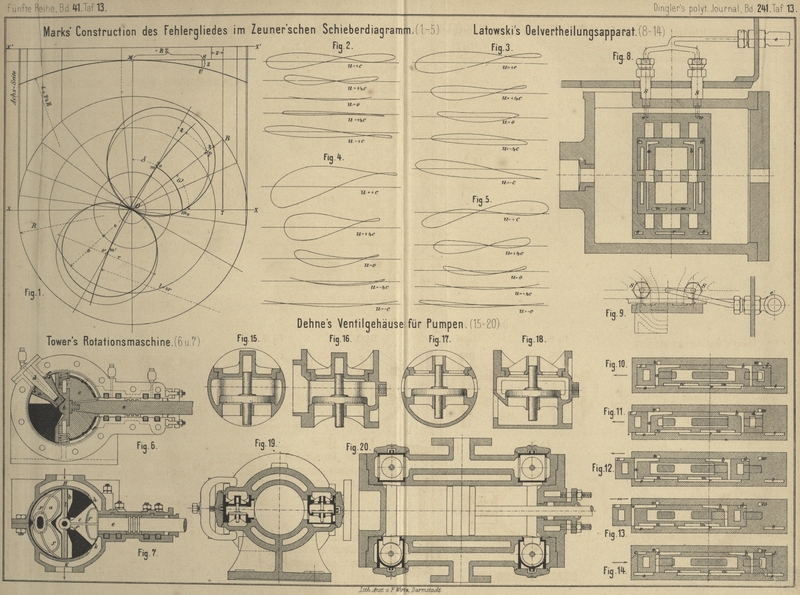
l als Radius und es ergibt sich die in Fig.
1 Taf. 13 dargestellte einfache Construction.
Die Schieberkreise o und o'
sind mit dem Voreilwinkel δ und dem halben Excenterhub
als Radius in normaler Weise aufgetragen. Die Kreise der inneren und äuſseren
Deckung, der äuſseren Kanalkante und des Kurbelzapfens ergaben die verschiedenen
kritischen Punkte und die Projectionen vom Kreise R auf
die parallel zur X-Achse gezogene Linie X'X' die entsprechenden Kolbenstellungen für unendlich
lange Excenter- und Treibstangen.
Um nun zunächst das Fehlerglied der Steuerung zu construiren, wird über der
Mittellinie oo' der Schieberkreise das betreffende
Parabelstück aufgetragen, dessen Scheitel um den Betrag
\frac{C}{2\,l} hinter dem Ursprung O liegt. Nachdem jedoch noch die zweite Bestimmung besteht, daſs für die
todten Punkte z=0 wird, so ist es einfacher mit dem Werthe
\xi=Om_0 die Stücke Om und Om' auf der Linie oo'
abzuschneiden und durch diese den Kreis vom Radius l zu
legen. Für einen beliebigen Kurbelwinkel ω wird der
Werth von z erhalten, indem das Stück OP auf der Linie oo'
abgeschnitten und der Abstand des Parabelbogens genommen wird; diese Maſse, je nach
der Lage der Curve positiv oder negativ vom Schieberkreis auf die Radienvectoren
aufgetragen, geben endlich zwei neue kreisähnliche Curven, welche die wahren
Schieberausschläge darstellen. Dieselben tangiren nicht mehr die Normale auf die
Schieberkreismittellinie und gehen auch nicht mehr nothwendig durch den Punkt O.
Obwohl in Folge des ungewöhnlichen Excenterstangenverhältnisses
l:r=4 das Fehlerglied auſsergewöhnlich groſs ist, macht sich
dessen Einfluſs nicht allzu sehr geltend; bei guten Steuerungen ist dieser Werth 20,
30 und mehr und läſst sich das Fehlerglied absolut nicht mehr nachweisen. Uebrigens
ist es bei den hier angenommenen grellen Verhältnissen interessant zu bemerken, wie
der Einfluſs des Fehlergliedes an den beiden Cylinderenden gerade entgegengesetzt
ist. So wird der obere Schieberkreis gröſser, der untere kleiner, und während für
das der Achse abgewendete Cylinderende der Maximalausschlag die Compression und die
Vorausströmung vergröſsert, die Voreinströmung und die Füllung verkleinert wird,
findet für die Achsseite des Cylinders in allen Punkten das gerade Entgegengesetzte
statt. Doch ist hervorzuheben, daſs der in diesem speciellen Falle charakterisirte
Einfluſs des Fehlergliedes nicht immer gleich auftritt und unter Umständen die
Aenderungen des Füllungsgrades auch umgekehrt auftreten können.
In gleicher Weise wie die endliche Excenterstangenlänge berücksichtigt Prof. Marks auch die endliche Treibstangenlänge und entwickelt aus der
allgemeinen Gleichung derselben:
x=R\,(1-cos\,\omega)-\frac{R^2}{2\,L}\,sin^2\,\omega
die Formel für das Fehlerglied Z,
nämlich: (R\ sin\ \omega)^2=2\ LZ.
Der Werth R sinω läſst sich direct aus dem Diagramm
abstechen; für die Parabel wird ein mit dem Scheitel in M geschlagener Kreis vom Radius L gezogen und
der Abstand SU = Z gibt
sofort den Betrag, um welchen der Kolben näher der Achse rückt als wie er bei
unendlich langer Treibstange stehen würde. Hier ergibt sich sofort, um wie viel mehr
die endliche Schubstange den Füllungsgrad an beiden Cylinderenden beeinfluſst, so
daſs gerade aus diesem Grunde das Justiren auf gleiches Voreilen im Allgemeinen
unzulässig wird.
In ähnlicher Weise hat Marks auch den Einfluſs studirt,
welchen bei Coulissensteuerungen die Anordnung des Excenterstangenangriffes hinter der Mittellinie des Coulissenbogens
hervorbringt, und vergleicht die Richtigkeit all seiner Entwicklungen durch die
entsprechenden direct vom Modell als Polardiagramme aufgezeichneten Diagramme.
Von speciellem Interesse sind noch die Untersuchungen, welche an demselben Modelle
angestellt wurden über die störenden Bewegungen des Coulissensteins bei
verschiedenen Arten der Aufhängung einer Stephenson'schen Coulisse. Auf Taf. 13
zeigt Fig. 2 das vom Apparat geschriebene Diagramm des Coulissensteins für eine
Stephenson-Coulisse mit Angriff der Excenterstange in der Mittellinie des
Coulissenbogens und Angriff des Hängeeisens in der Mitte des Bogens, Fig. 3
dieselbe Coulisse in der Mitte der Sehne aufgehängt, Fig. 4 im
unteren Excenterstangenbolzen und Fig. 5
halbwegs zwischen diesem und dem Coulissenmittel, aber auch in der Mittellinie des
Bogens aufgehängt. Die Curven folgen sich von oben nach unten entsprechend der
tiefsten Stellung der Coulisse (Ausschlag des Steins u
= c, halbe Coulissenlänge) bis zur höchsten Stellung
und geben ein klares Bild der dabei auftretenden Veränderungen, deren Einfluſs wohl
kein Diagramm jemals vollständig darstellen wird.
Tafeln