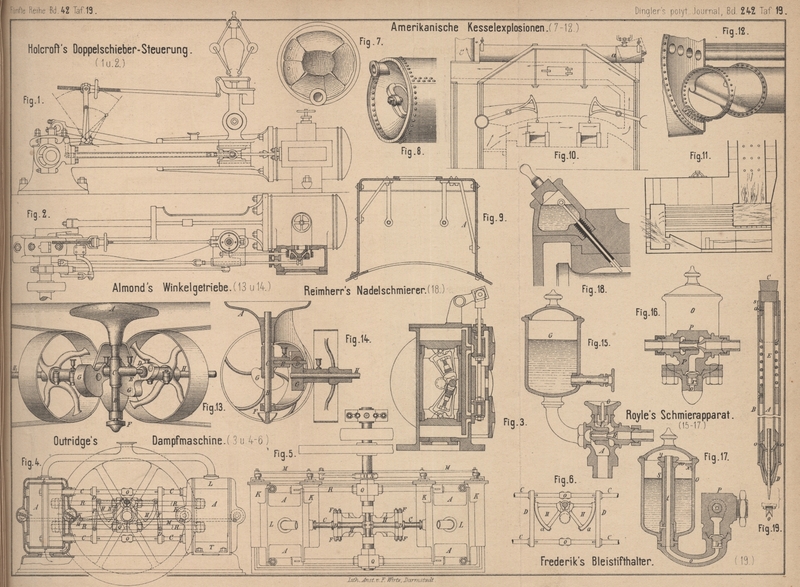
| Titel: | Doppelschieber-Steuerung von G. Holcroft in Niederbronn, Elsass. |
| Autor: | Müller-Melchiors |
| Fundstelle: | Band 242, Jahrgang 1881, S. 233 |
| Download: | XML |
Doppelschieber-Steuerung von G. Holcroft in
Niederbronn, Elsaſs.
Mit Abbildungen im Text und auf Tafel 19.
Müller-Melchiors, über Holcroft's
Doppelschieber-Steuerung.
Die von G. Holcroft, Maschinenfabrik in Niederbronn,
Elsaſs, erfundene Doppelschieber-Steuerung bewirkt die Verstellung der Expansion
durch Veränderung von Voreilung und Hub des idealen Expansionsexcenters, welches der
vom Vertheilungsschieber durch Hebelcombination abgeleiteten Bewegung der
Expansionsplatte zu substituiren ist.
In einer Verlängerung des Excenterringes befindet sich hier eine kurze Hebelwelle
gelagert, deren nach abwärts gerichteter Arm die Expansionsschieberstange erfaſst,
während der horizontale Arm von einem Lenker geführt wird. Bei der in Fig.
1 Taf. 19 gezeichneten Aufhängung des Lenkers steht für die beiden
extremen Excenterstellungen der untere Hebelarm genau vertical und damit die
Expansionsplatte genau über der Mitte des Grundschiebers (vgl. Fig. 2). Bei
Weiterdrehung der Kurbel in der Pfeilrichtung kommt das Excenter sammt der
Winkelhebelwelle nach abwärts und so muſs, da ihr oberer Arm an seinem Ende nahezu
horizontal geführt wird, der abwärts gerichtete Arm nach rechts ausschlagen und so
die Expansionsplatte aus der Mittelstellung nach rechts schieben und endlich den
Dampfabschluſs bewirken. Verstellt man den Drehpunkt des Lenkers nach rechts, so
daſs das Ende des Winkelhebels auf eine von links nach rechts abfallende Curve (in
Fig. 1 punktirt) geführt wird, so ist schon vor Erreichung der in Fig. 1
gezeichneten Stellung die Expansionsplatte auf ihrem Schiebergesicht so weit nach
rechts verschoben worden, daſs Schluſs bewirkt wurde; bei der entgegengesetzten
Verstellung des Lenkerdrehpunktes wird das Eintreten des Dampfabschlusses hinaus
gerückt.
Die Einwirkung des Lenkerarmes ist, falls derselbe im Verhältniſs zum Excenterhub
nicht allzu kurz ist, derjenigen einer geraden Coulisse gleich zu setzen, welche
durch den Regulator verdreht wird und so die Veränderung des Füllungsgrades bewirkt.
Unter dieser Voraussetzung und mit der Annahme einer unendlich langen Excenterstange
ergibt sich für die Kurbelstellung ω über dem todten
Punkt der Ausschlag des abwärts gerichteten Winkelhebelarmes aus seiner verticalen
Stellung und hiermit
der relative Weg der Expansionsplatte gegenüber dem Grundschieber:
\xi=b\,sin\,\gamma.
Zur Bestimmung von γ dienen die Gleichungen:
r\,cos\,(\omega+\delta)=c\,sin\,\gamma+u\,sin\,\alpha
und
r\,sin\,(\omega+\delta)-c\,(1-cos\,\gamma)=u\,cos\,\alpha,
in welchen cos\;\gamma=1 gesetzt und u eliminirt wird, worauf:
c\,sin\,\gamma=\frac{r}{cos\,\alpha}\,cos\,(\omega+\delta+\alpha).
Für die Verdrehung der Coulisse nach der entgegengesetzten
Seite wird:
c\,sin\,\gamma=\frac{r}{cos\,\alpha}\,cos\,(\omega+\delta-\alpha).
und somit die allgemeine Gleichung für den relativen
Schieberweg der Expansionsplatte: \xi=\frac{b}{c}\
\frac{r}{cos\,\alpha}\,cos\,(\omega+\delta\,\pm\,\alpha).
Die Gleichung kann direct nach sin ω und cos ω aufgelöst und in gewöhnlicher Weise durch das
Zeuner'sche Schieberdiagramm dargestellt werden, indem für wechselnde
Coulissenwinkel α die entsprechenden Coordinaten der
Centralcurve ausgerechnet werden.
Fig. 1., Bd. 242, S. 234
Fig. 2., Bd. 242, S. 234
In rein graphischer Ausführung ist im Diagramm Textfigur 2 der Voreilwinkel δ des Vertheilungsexcenters von der Todtpunktlage der Kurbel nach
rückwärts aufgetragen und darauf als Fahrstrahl die Länge
\frac{b}{c}\,r abgeschnitten. Für die Coulissenstellung der
Textfigur 1 wird dann der Winkel α weiterhin nach rückwärts aufgetragen und darauf der
Werth \frac{b}{c}\,\times\,\frac{r}{cos\,\alpha} durch die auf
dem ersten Fahrstrahl errichtete Senkrechte abgeschnitten. Das mit diesem
Durchmesser und unter dem Winkel α + δ nach beiden Seiten des Coordinatenursprunges
gezeichnete Kreispaar entspricht in jedem unter dem Winkel ω
gezogenen Fahrstrahl der Gleichung des relativen Schieberweges. Die
Schnittpunkte mit dem Ueberdeckungskreis (nach Fig. 2 Taf.
19 negativ) bezeichnen Eröffnung und Schluſs der Dampfkanäle des Grundschiebers und sind in Textfigur 2 für die Horizontalstellung der Coulisse
und für die Verdrehung derselben unter dem Winkel α
abwärts und aufwärts von der Horizontalen angegeben.
Wie hier ersichtlich, lassen sich schon mit kleinen Verdrehungswinkeln der Coulisse
weite Füllungsgrenzen erzielen und kann daher die Holcroft'sche Steuerung auch von diesem Gesichtspunkte aus als vorzüglich
gelungen bezeichnet werden.
Müller-Melchiors.
Tafeln