| Titel: | Klinkerfues' rectificirender Planimeter, Ellipsograph und Pantograph. |
| Autor: | H–s. |
| Fundstelle: | Band 242, Jahrgang 1881, S. 413 |
| Download: | XML |
Klinkerfues' rectificirender Planimeter, Ellipsograph und
Pantograph.
Mit Abbildungen auf Tafel 33.
Klinkerfues' rectificirender Planimeter, Eilipsograph und
Pantograph.
Der von W.
Klinkerfues in Göttingen (* D. R. P.
Kl. 42 Nr. 13646 vom 16. Juli 1880) erfundene Planimeter, welcher auch als
Ellipsograph und Pantograph benutzt werden kann, bestimmt gleichzeitig Fläche und
Umfang einer mit ihm
umschriebenen Figur, weshalb ihn der Erfinder „rectificirend“ nennt.
Die mathematische Begründung des neuen Instrumentes ist eine ziemlich einfache. Wird
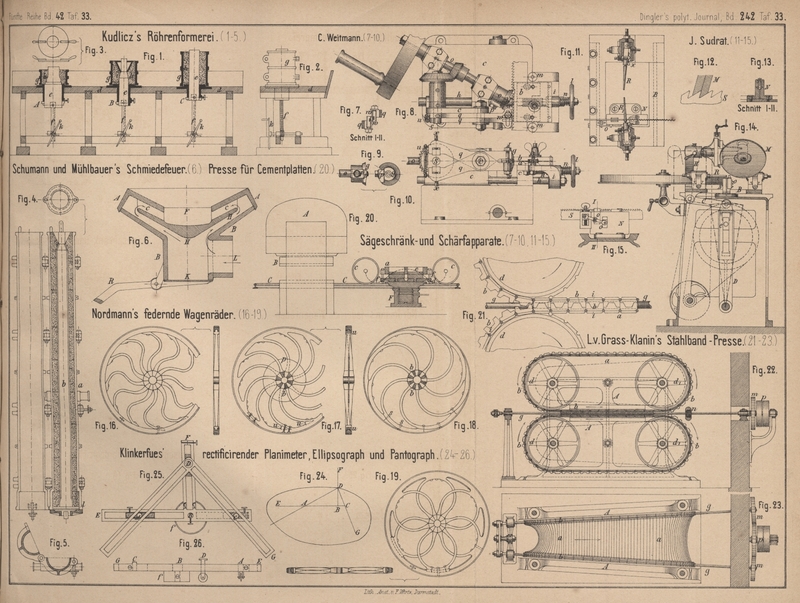
in dem rechtwinkligen Dreiecke ADC (Fig.
24 Taf. 33) aus D das Perpendikel DB auf die Hypothenuse AC gezogen, so ist BD die mittlere geometrische Proportionale zwischen AB und BC.
Macht man nun BC constant und gleich der Einheit,
so ist für verschiedene Werthe von DB und AB immer
\overline{AB}=\overline{DB^2}. Ist nun A auf EB und D auf FB und C auf DG
verschiebbar, kann sich ferner die ganze Figur um B
drehen, so läſst sich D auf einer Curve herumführen.
Betrachtet man B als Pol, so ist BD ein Radiusvector, also BD = r und nach dem
früheren AB = r2. Bei der Drehung des Systemes um den Winkel dφ beschreibt D auf der
Curve das Längenelement \sqrt{r^2d\varphi+dr^2} und A gleichzeitig ein anderes Längenelement
\sqrt{r^4d\varphi^2+4\,r^2dr^2}, dessen zu AB senkrechte Componente sich durch r2 dφ oder das
doppelte von dem Radiusvector r beschriebene
Flächenelement ausdrückt. Denkt man sich nun in D ein
Rädchen angebracht, welches nach allen Seiten frei beweglich ist, und in A ein Rädchen, dessen Scheibe immer senkrecht zu AB festgehalten wird, damit seine Drehung nur die
Normalbewegung auf AB zum Ausdruck bringt, so wird der von der Rolle D durchlaufene Weg dem Umfang und der von der Rolle A durchlaufene Weg der Fläche der umschriebenen Figur
entsprechen.
Diesem Princip entsprechend ist das Instrument in der aus den Fig. 25 und
26 Taf. 33 der Hauptsache nach ersichtlichen Weise ausgeführt. Ein mit
Schlitzen versehenes Kreuzstück EFC ist um den
Zapfen B drehbar, welcher in einem mit Blei
ausgegossenen Fuſs f befestigt ist. In den Schlitzen
des Kreuzstückes sind drei Schlitten verschiebbar, von denen einer durch einen
Bolzen D mit dem Scheitel eines rechtwinkligen Stückes
verbunden ist, während die beiden anderen mit Zapfen A
und C in die geschlitzten Schenkel dieses Winkelstückes
eingreifen. Nachdem der Zapfen C so eingestellt ist,
daſs BC gleich der Einheit ist, wird der ihn
tragende Schlitten im Kreuzstück mittels einer Klemmschraube festgebremst. An dem
mit dem Zapfen A versehenen Schlitten ist eine Rolle
angebracht, welche sich nur in einer zu EB
senkrechten Ebene drehen kann, während die an dem Zapfen D angebrachte Rolle vermöge der Drehbarkeit des Zapfens beständig in der
Richtung der Elemente der umschriebenen Curve gehalten werden kann. Selbstredend
müssen Schlitten und Zapfen in den Schlitzen möglichst ohne Reibung gehen. Alles
hierauf bezügliche, sowie das Zählwerk sind in den Abbildungen weggelassen. Die
Rolle bei D kann auch durch einen Fahrstift ersetzt
werden, wenn man auf die Rectificirung der Curve verzichten will.
Wird das Kreuzstück auf dem Drehzapfen B festgebremst
und der Schlitten mit
dem Zapfen A im Kreuzstück festgestellt, so kann der
Punkt D nur noch einer Ellipsenhälfte folgen, deren
groſse Achse AC und deren Achsenverhältniſs AB : BC ist. Nach dem
Lösen von B kann das Instrument um 180° herumgedreht
werden, worauf der Zapfen B wieder festzubremsen und
die andere Hälfte der Ellipse mit dem Punkt D zu
beschreiben ist. Vor der Benutzung des Instrumentes als Ellipsograph ist der Schlitz
des Kreuzstückschenkels BF durch Drehen der
Schraube F etwas zu erweitern; die den Schenkel
bildenden Schienen drehen sich hierbei um zwei Gelenke e.
Löst man die Klemmschrauben bei A, B und C und befestigt man den Winkel an dem Gleitstück bei
D, so ist das Instrument auch als Pantograph zu
gebrauchen, weil dann die Punkte D und C einander ähnliche Curven beschreiben müssen. Die
Verjüngung wird durch den stellbaren Winkel BDG
bestimmt.
H–s.
Tafeln