| Titel: | Untersuchungen über das Verhalten des Phosphorbronzedrahtes bei der Beanspruchung durch Zugkräfte; von Professor H. Fischer in Dresden. |
| Autor: | H. Fischer |
| Fundstelle: | Band 245, Jahrgang 1882, S. 64 |
| Download: | XML |
Untersuchungen über das Verhalten des
Phosphorbronzedrahtes bei der Beanspruchung durch Zugkräfte; von Professor H. Fischer in
Dresden.
Mit Abbildungen auf Tafel 7.
H. Fischer, über Untersuchungen des
Phosphorbronzedrahtes.
Verschiedene Aufsätze in dieser und anderen technischen ZeitschriftenVgl. Dingler's polytechnisches Journal, 1882 248 432. 244 408.
Elektrotechnische Zeitschrift. 1882 S. 73. 127.
157.
Engineering, 1881 Bd. 32 S. 430. 1882 Bd. 33 S.
192. weisen auf die Wichtigkeit hin, welche der
Phosphorbronzedraht in der Neuzeit für die Anlegung von Telephonleitungen erlangt
hat. Die Verfasser suchen die Zweckmäſsigkeit dieses Materials für genannten Zweck
durch Zahlen zu
belegen, welche auf Versuchen zur Ermittelung der elektrischen Leitungsfähigkeit und
der Widerstandsfähigkeit gegen Zugkräfte basiren. Daſs hierbei auch gegentheilige
Meinungen und Anschauungen Ausdruck finden, ist natürlich und erklärlich, da die
Untersuchungen der einzelnen Beobachter an verschiedenen Versuchsobjekten zur
Ausführung gelangten, denen eine völlige Materialgleichheit wohl kaum zugestanden
werden kann. Die Unsicherheit der erhaltenen Resultate wird aber, wenigstens in
Bezug auf die Festigkeitsuntersuchung, wesentlich noch durch den Umstand erhöht,
daſs selbst bei ein und demselben Material, je nach der physikalischen
Beschaffenheit desselben, wesentlich abweichende Ergebnisse erzielt werden. Der
Einfluſs des Arbeitsverfahrens, welches bei der Herstellung des Versuchsstückes
Anwendung fand, ist in dieser Hinsicht allseitig bekannt.
Im Folgenden sollen die Ergebnisse einer Untersuchung von Phosphorbronzedrähten aus
der Fabrik von Lazare Weiller zu Angoulême in
Frankreich zur Kenntniſs gebracht werden, welche geeignet sein dürften, die
wesentlichen Aenderungen der Festigkeits- und Elasticitätsverhältnisse durch das bei
der Vorrichtung der Versuchsobjecte beobachtete Arbeitsverfahren anschaulich zu
machen. Das Versuchsmaterial wurde mir auf specielles Ansuchen durch den Vertreter
der genannten Fabrik, Hrn. J. B. Grief in Wien, mit
dankenswertester Bereitwilligkeit zur Verfügung gestellt. Die Untersuchung
erstreckte sich auf 10 Drahtproben. Fünf derselben waren durch Ausglühen nach dem
Ziehen erweicht; den übrigen waren durch verschieden oftes Passiren eines Drahtzuges
verschiedene Härtegrade ertheilt worden. Die Beobachtungen wurden mit Hilfe eines
selbstregistrirenden Zerreiſsapparates nach Reusch
(1880 235 * 414) des mechanisch-technologischen
Laboratoriums der Dresdner technischen Hochschule durchgeführt. Die mit diesem
Apparat erhaltenen Diagramme geben den Zusammenhang der Streckungen mit den
dieselben erzeugenden Belastungen in jedem Augenblick des Versuches an und somit ein
getreues Bild der während der Beanspruchung auftretenden Erscheinungen. Die gröſste
Abscisse repräsentirt die Strecke, um welche sich das Versuchsstück bei dem Eintritt
des Bruches verlängert hat, also die Bruchdehnung δ;
die zu dieser gehörende Ordinate miſst die für Herbeiführung des Bruches nöthige
Belastung p. Die Diagrammordinaten wachsen stetig von
Null bis p, während gleichzeitig die Abscissen
(Dehnungen) von Null bis S zunehmen. Der Verlauf der
Curve charakterisirt das der Untersuchung unterworfene Material.
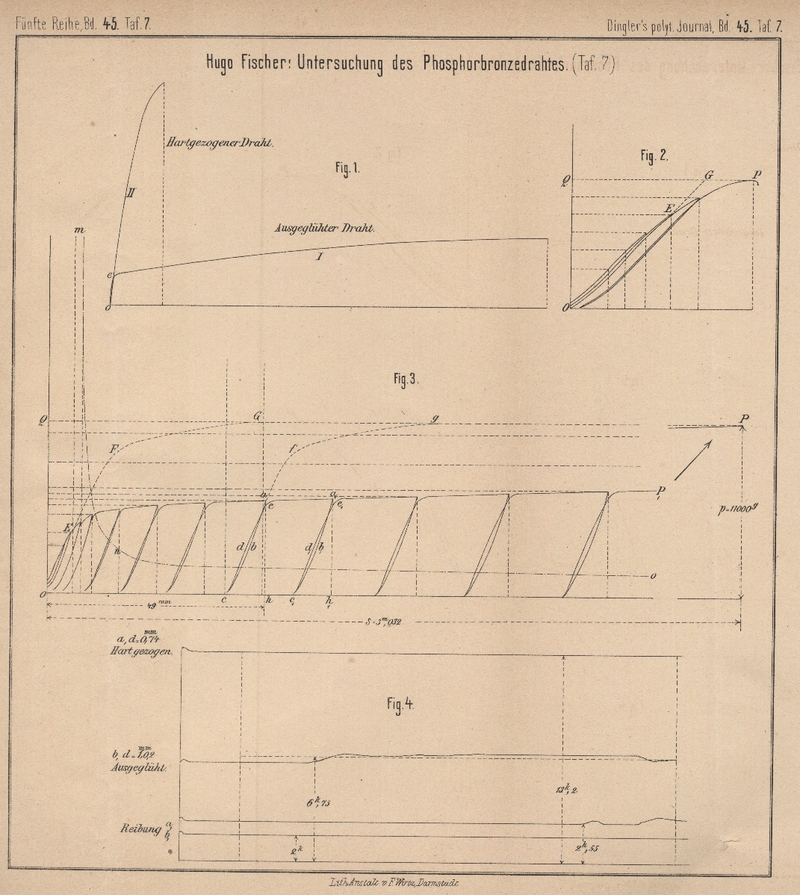
Fig.
1 Taf. 7 zeigt die wesentliche Verschiedenheit des Curvenlaufes für
ausgeglühten und durch Ziehen hart gewordenen Phosphorbronzedraht von 0mm,42 Durchmesser und 324 bezieh. 800mm Länge. Die Curve I, dem geglühten Draht angehörend, steigt im Anfang der Belastung in Folge der
Starrheit des Materials rasch bis e und wendet sich
dann gegen die Abscissenachse, dieser in einem langen Zuge folgend. Der Curvenzug II, bei der Untersuchung des harten Drahtes erhalten,
zeigt nur eine rasche Steigung und endet schlieſslich bei kleiner Abscisse und
groſser Ordinate an der Bruchgrenze. Der Eintritt der Richtungsänderung bei Curve
I bezeichnet den Beginn des Flieſsens der
Materialtheilchen. Vor demselben ist die Streckung eine rein elastische, nach deren
Aufhören der Draht unter Wirkung der inneren Kräfte seine ursprüngliche Länge wieder
annimmt. Im weiteren Verlauf tritt eine gegenseitige Verschiebung der benachbarten
Materialtheilchen, das Flieſsen derselben, ein. In
Folge dessen erfährt der Draht eine bleibende Längenänderung bei gleichzeitiger
Querschnittsverminderung, welche auch nach Wegnahme der äuſseren Kraft nicht wieder
vollständig verschwindet und die ihren gröſsten Werth an der Bruchgrenze erreicht.
Da bis zum Eintritt des Flieſsens die Längenänderungen rein elastische sind, so
fällt derselbe mit der Elasticitätsgrenze des Materials zusammen.
Zwischen Elasticitäts- und Bruchgrenze erleidet das auf Zug beanspruchte Material
sowohl bleibende, als elastische Dehnung, deren Gröſse durch mehrfache Entlastungen
während des Versuches bestimmt werden kann. Innerhalb der Elasticitätsgrenze ist für
eine bestimmte Beanspruchung das Verhältnis der elastischen Dehnung δe zu der bleibenden
Dehnung δb, da die
letztere gleich Null, unendlich groſs. Dasselbe nimmt aber nach Ueberschreitung
dieser Grenze rasch ab und erreicht an der Bruchgrenze den kleinsten Werth, wie dies
der Curvenzug mno in Fig. 3
zeigt. Hierbei ist:
\frac{\delta_e}{\delta_b}=f\,(\delta_e+\delta_b)=f\,(\delta)
also als Funktion der den Belastungen äquivalenten
Gesammtdehnungen eingetragen. In derselben Figur ist ferner OEP1
→
P eine Copie des Originaldiagrammes, das bei der
Belastung eines ausgeglühten Phosphorbronzedrahtes von 5m,482 Anfangslänge und 0mm,67 Dicke
erhalten wurde. Die Curve OEP1 stellt nur den ersten, in unmittelbarer Nähe der Elasticitätsgrenze
liegenden Theil des Gesammtdiagrammes dar; letzteres würde, bei einer an anderer
Stelle beobachteten mittleren Bruchdehnung des ausgeglühten Phosphorbronzedrahtes
von δ = 55,3 Proc., eine Länge von 3m,032 besitzen. Der Curvenzug EP, welcher die Elasticitätsgrenze mit der Bruchgrenze
verbindet und der Figur zu Folge annähernd geradlinig verläuft, endet an letzterer
in einem Abstand von der Abscissenachse welcher einer Bruchbelastung von etwa
11000g entspricht. Während der Aufzeichnung
dieses Diagrammes wurden behufs Ermittelung der Lage der Elasticitätsgrenze mehrfach
Entlastungen vorgenommen. Hierbei folgte der Schreibstift des Zerreiſsapparates den
Linien abc, a1
b1
c1...... und kehrte
dann bei erneuter Belastung auf dem Wege cde, c1
d1
e1.... wieder zurück.
Der Abstand des Schnittpunktes c der Entlastungslinie
mit der Abscissenachse von der durch den betreffenden Endpunkt der Diagrammcurve auf
die genannte Achse gefällten Normalen eh ist das Maſs des elastischen
Theiles der Dehnung Oh, welche der Draht durch die
Belastung bis e erlitt.
Trägt man die Werthe ch der elastischen Dehnung, die bei
verschiedenen Entlastungen erhalten wurden, als Funktion der Belastungen auf, welche
zu ihrer Erzeugung erforderlich waren, so erhält man den in Fig. 3
gezeichneten Curvenzug EFG, welcher Aufschluſs über das
elastische Verhalten des Drahtes bei Beanspruchungen zwischen der Elasticitäts- und
Bruchgrenze gibt und die Diagrammcurve bei E schneidet.
In diesem Schnittpunkt ist die bleibende Dehnung Null, es stellt derselbe somit auf
der Diagrammcurve die Lage der Elasticitätsgrenze fest. Die Fläche OEFGQ = Fe repräsentirt den elastischen Theil der gesammten
Formänderung im Verlauf der Beanspruchung, die Fläche EFGP =
Fb gibt in ihrer Gestalt ein Bild und in
ihrer Gröſse ein Maſs für das Auftreten der unelastischen Formänderungen während der
allmählichen Belastung bis zur Bruchgrenze. Das Verhältniſs:
\varepsilon=F_e\,:\,F_b
stellt somit das elastische Verhalten oder den Elasticitätsgrad des untersuchten Drahtes dar. Ist e groſs, sind also die elastischen Formänderungen
vorherrschend, so ist der Draht stark elastisch. Für einen bis zum Eintritt des
Bruches vollständig elastischen Körper würde Fb = Null, daher e = ∞
sein; Fe = Null, also
ε = Null charakterisirt dagegen einen bis zum
Eintritt des Bruches vollständig unelastischen Körper.
Eine anderweite Charakteristik des Drahtes wird durch die Gröſse der gesammten
Streckung gewonnen, welche derselbe bei dem Eintritt des Bruches erfahren hat. Ein
geringer Betrag der Bruchdehnung charakterisirt den Draht als spröd, ein erheblicher
als zäh und es stellt somit die Zahl:
Z=100\,\delta\,:\,l,
d. i. die Gesammtdehnung S des
Probestückes, ausgedrückt in Procent der Anfangslänge l, den Zähigkeitsgrad des Materials dar.
Der Draht, oder allgemein jeder Körper, ist zäh elastisch oder spröd elastisch, je
nachdem eine gröſse oder kleine Zähigkeit mit starker Elasticität gepaart ist.
Entscheidend ist hierfür die Gröſse des bleibenden beziehentlich elastischen Theiles
der Gesammtdehnung an der Bruchgrenze. Zäh- beziehungsweise spröd-elastische Körper zeigen Vorherrschen des elastischen
Theiles δe gegenüber
dem bleibenden Theil δb
der Gesammtstreckung, bei zähen, beziehentlich spröden wenig
elastischen Körpern waltet das Gegentheil ob. Beispiele für diese
Körperzustände sind:
Vulkanisirter Kautschuck (zäh elastisch)
Z =
558%
δe =
95%
δb =
5%
von δ
Feuchtes Fichtenholz (spröd elastisch)
Z =
0,757
δe =
84
δb =
16
„
Geglühter Phosphorbronzedraht (zäh, wenig
elastisch)
Z =
55,3
δe =
1
δb
=
99
„
Alluminiumdraht (spröd, wenig elas- tisch)
Z=
6,5
δe
=
3
δb
=
97
„
Besitzt ein Körper die Eigenschaft unter der Einwirkung äuſserer Kräfte mit
Sicherheit bleibende Deformationen von gröſserem Betrage anzunehmen, wie feuchter
Thon, Wachs, glühendes Schmiedeisen u. dgl. so nennt man denselben bildsam. Die
Bildsamkeit ist um so gröſser, je kleiner die Kraft ist, welche die ersten
bleibenden Formänderungen erzeugt (abhängig von der Lage der Elasticitätsgrenze und
damit vom Tragmodul des Materials), je geringer der nach dem Aufhören der
Kraftwirkung wieder verschwindende Theil der Gesammtdeformation ist (abhängig von
dem Elasticitätsgrad) und je gröſser die Formänderung überhaupt ohne Lösung des
Zusammenhanges der kleinsten Theile sein kann, d.h. allgemein, je weniger elastisch
und je zäher der Körper ist. Der einem Körper eigene Grad von Bildsamkeit kann somit
proportional dem Zähigkeitsgrad Z und umgekehrt
proportional dem Elasticitätsgrad ε und Tragmodul Tl gesetzt und daher
durch den Quotienten:
B=Z\,:\,\varepsilon T_l
zum Ausdruck gebracht werden. Die häufig schwierige Bestimmung
des Querschnittes vom Versuchsstück läſst es zweckmäſsig erscheinen, den Tragmodul
T nicht durch die gewöhnlich übliche Belastung auf
die Flächeneinheit auszudrücken, sondern nach Analogie der Reiſslänge durch
diejenige Länge des Versuchsstückes in Kilometer, deren Gewicht eine Streckung des
Stückes bis zur Elasticitätsgrenze herbeiführen würde. Zur Unterscheidung ist für
denselben die Bezeichnung Tl gewählt.
Bestimmte Zahlenwerthe, welche die Grenzen festsetzen, innerhalb deren ein Körper
zäh, spröd, bildsam oder elastisch genannt wird, müssen durch Untersuchung einer
gröſseren Zahl solcher Körper ermittelt werden, denen die Technik die betreffenden
Eigenschaften zuerkennt. Natürlich gelten diese Betrachtungen vor der Hand nur für
Zugbeanspruchungen; anderweite Versuche scheinen jedoch darauf hinzudeuten, daſs
dieselben auch für Druck- und Schubbeanspruchungen Gültigkeit behalten.
Für den vorliegenden geglühten Phosphorbronzedraht stellt sich:
Z=\frac{100\delta}{l}=55,3\,\%,\
\varepsilon=\frac{F_e}{F_b}=0,014,\ T_l=1^{km},37,\
B=\frac{Z}{\varepsilon\,T}=2765
Die Entlastungslinie abc (Fig. 3) und
die neue Belastungslinie cde fallen vor und in
unmittelbarer Nähe der Elastizitätsgrenze selbst bei der vorliegenden groſsen Länge
des Versuchsstückes zusammen, weichen aber um so mehr von einander ab, je weiter
entfernt von der Elasticitätsgrenze die Entlastung bewirkt wurde. Die
Entlastungscurve ist stets convex gegen die Abcissenachse, während die neue
Belastungscurve dieser Achse die concave Seite zukehrt. Das Abweichen der Curve
gegen den Coordinatenursprung hin ist die Folge der Elasticität des Materials. Die
Erklärung für die convexe Gestalt der Entlastungscurve dürfte vielleicht in dem
Umstand zu suchen sein, daſs die Körpermolecüle, welche durch die spannende Kraft in
Bewegung gesetzt wurden, einen Theil der aufgewendeten Arbeit in Form lebendiger
Kraft in sich aufgenommen haben. Diese wird bei der Entlastung die Arbeitsfähigkeit der
abnehmenden äuſseren Kraft unterstützen und dazu beitragen, daſs die innere Reibung
des Körpers überwunden und die bereits vorhandene Bewegung der kleinsten Theile (das
Flieſsen) noch weiterhin unterhalten wird (NachwirkungsdeformationVgl. Dr. P. Schmidt: Ueber die innere Reibung fester
Körper. (Breslau 1880. Verlag von A.
Gosohorsky.)). An der Elasticitätsgrenze geht die
Entlastungslinie durch den Coordinatenursprung O. Die
mehrfachen, sich folgenden Entlastungen deuten auf eine Aenderung der Constitution
des Versuchsstückes hin, sobald die Elasticitätsgrenze überschritten, also das
Flieſsen der kleinsten Materialtheilchen eingetreten ist. Diese Aenderung gibt sich
durch die Erhöhung der Elasticitätsgrenze deutlich kund. Bei dem ausgeglühten
Phosphorbronzedraht, welcher das Diagramm Fig. 3
lieferte, wird z.B. nach Ausweis des Diagrammes die Elasticitätsgrenze bei einer
Belastung von p' = 4500g und einer Dehnung Δ = 1/914
l erreicht. Es tritt jedoch bei demselben Draht das
Flieſsen erst bei einer Belastung p1 = 6100g und
einer Längenänderung Δ1
= 1/623
l ein, wenn nach einer Reckung um 49mm eine Entlastung und neue Belastung erfolgte.
Der Schnittpunkt der nach Analogie der Curve EFG
construirten neuen Curve efg, für welche der
Coordinatenanfang bei c liegt, mit der neuen
Belastungslinie cde gibt im Diagramm die Lage der neuen
Elasticitätsgrenze ziemlich sicher an. Dieselbe fällt mit dem Schnittpunkt der
Curven abc, cde zusammenDie Lage dieses Punktes wird durch die Länge der Beobachtungszeit
beeinfluſst, da bekanntlich erst in längeren Zeiträumen, nach Tagen, Wochen,
ja selbst Monaten, die in ihrer gegenseitigen Lage gestörten Molecüle eines
Körpers den anfänglichen oder einen neuen Gleichgewichtszustand erreichen.
Bei genügend dauernder Ruhe nach der Entlastung würde die neue
Belastungscurve in Folge der elastischen Nachwirkung jedenfalls wieder durch
den Anfang der Entlastungscurve oder in dessen Nähe vorübergehen. Hiermit
ist auf eine den vorliegenden Untersuchungen anhaftende Ungenauigkeit
hingewiesen, der zu Folge die elastischen Aenderungen der Drahtlänge um ein
geringes zu klein erhalten wurden. Da diese Arbeit jedoch schon in Folge der
zur Untersuchung benutzten Hilfsmittel nicht den Anspruch auf höchste
wissenschaftliche Genauigkeit erheben kann, vielmehr zur Aufklärung der technischen Eigenschaften des untersuchten
Materials beizutragen bestimmt ist, so wurde von dem voraussichtlich erst
nach Tagen oder Wochen merkbaren Einfluſs der Zeit abgesehen und die Be- und
Entlastungen zwar langsam (sekundliche Geschwindigkeit des Schreibstiftes
etwa 0mm,3), aber in unmittelbarer Folge
auf einander vorgenommen., so daſs von diesem aus das erneute
Flieſsen der Materialtheilchen beginnt, was sich durch die raschere Ablenkung der
Curve nach rechts zu erkennen gibt. Das Flieſsen tritt im vorliegenden Fall also
bereits bei einer geringeren Belastung wieder ein, als die bei dem Beginn des
Entlastens vorhandene war. Der Schnittpunkt c auf der
Abscissenachse ist der Anfangspunkt einer neuen Diagrammcurve, welche ein
gleichstarker geglühter Draht liefern würde, wenn man denselben vor der Untersuchung
durch die Belastung p1
auf die Länge (l + Oc)
streckte. Der Flächeninhalt des vor dem
Entlastungspunkte liegenden Diagrammtheiles repräsentirt die Arbeitsgröſse, welche auf die
Zustandsänderung des Drahtes verwendet wurde.
Die Erkenntniſs, daſs bei genügender Dauer des Versuches die neue Belastungscurve
wieder durch den Entlastungspunkt gehen, oder sich in unmittelbarer Nähe an die alte
Spannungscurve anschlieſsen wird, führt zu einer Deutung der Curve EFG. Da durch dieselbe die bei einer gewissen Spannung
erreichte elastische Dehnung als Abhängige dieser Spannung dargestellt ist und da
diese elastische Dehnung die Streckung an der Elastizitätsgrenze eines Drahtes
bedeutet, welcher durch die betreffende Spannung aus einem Anfangszustand in einen
neuen (gespannten) Zustand übergeführt wurde, so erhellt, daſs der Verlauf der Curve
EFG das Gesetz der Veränderung der
Elasticitätsgrenze während der bis zum Bruch erfolgten Belastung des Drahtes
darstellt. Ich nenne diese Curve daher die Grenzcurve der
vollkommenen Elasticität oder kurz die Elasticitätscurve. Das Hauptdiagramm gibt hierbei gleichzeitig die
mechanische Arbeit an, welche für eine beabsichtigte Erhöhung der Elasticitätsgrenze
aufgewendet werden muſs.
Die Erhöhung der Elasticitätsgrenze nach Eintritt des Flieſsens der Molecüle weist
darauf hin, daſs mit der Erreichung der ersten
Elasticitätsgrenze die elastische Kraft des Materials noch nicht völlig erschöpft
ist. Dies zeigt deutlich der Lauf der Curve EFG
Fig.
3. Nach jeder Entlastung oberhalb der ersten Elasticitätsgrenze zeigt das
Versuchsstück ein anderes Verhalten als ursprünglich, was jedenfalls durch die
während des Flieſsens eingetretene Umlagerung der Molecüle bedingt ist. Für das so
aus dem ursprünglichen hervorgegangene neue Versuchsobject, dessen Gewicht das
gleiche geblieben, das den Längen- und Querschnittsdimensionen nach dagegen ein
anderes geworden ist, hat dem Diagramm zu Folge die bleibende Dehnung gegenüber der
zugehörigen elastischen Dehnung einen kleineren Werth als vorher. Die bleibende
Dehnung nimmt um so mehr ab auf Kosten der elastischen, je stärker das Stück bereits
gestreckt wurde, je näher der Entlastungspunkt also der Bruchgrenze liegt. Könnte
die letzte Entlastung unmittelbar an der Bruchgrenze, aber
noch vor Eintritt des Bruches bewirkt werden, so müſste den angestellten
Betrachtungen zu Folge die neue Belastungslinie durch die Bruchgrenze gehen und
hierbei natürlich der Bruch im Moment des Erreichens dieser Grenze stattfinden. Das
durch die Belastung bis dicht an die Bruchgrenze gestreckte Versuchsstück wird
demnach nur elastische Formänderung zeigen, dasselbe
ist ein vollkommen elastischer Körper geworden. Die Gröſse dieser elastischen Formänderung drückt daher gleichzeitig die Gröſse der
Elasticität aus, welche dem anfänglichen Versuchsstück überhaupt zukam; denn das
durch die Belastung und Streckung aus diesem hervorgegangene neue Versuchsstück ist
seinem Gewicht, also seiner Materialsubstanz nach völlig das gleiche geblieben.
Ist diese Auffassung richtig, so ist der Ausdruck Elasticitätsgrenze
für den Punkt, von
welchem aus bei der Belastung das durch bleibende Streckung wahrnehmbare Flieſsen
der Materialtheilchen beginnt, nicht zulässig, da die Untersuchung lehrte, daſs die
gesammte Elasticität des Versuchsstückes erst bei dem Eintritt des Bruches erschöpft
ist. Die Bruchgrenze bezeichnet daher ebenso die Elasticitätsgrenze, wie sie die
Flieſsgrenze darstellt. Hiermit wird dann natürlich auch der Begriff Erhöhung der Elasticitätsgrenze hinfällig. Bereits WertheimVgl. Poggendorff's Annalen, 1848 Ergänzungsband
2 S. 1 ff. hat durch Versuche nachgewiesen, daſs eine
Elasticitätsgrenze in dem gewöhnlich gebräuchlichen Sinne nicht besteht, daſs
vielmehr schon am Beginn der Belastung bleibende, wenn auch schwer meſsbare
Längenänderungen eintreten. Für die Untersuchung des vorliegenden Drahtes ist von
dieser Anschauung ein weiterer Gebrauch nicht gemacht, vielmehr dem praktischen
Bedürfniſs entsprechend dem Begriff Elasticitätsgrenze die gegenwärtig allgemein
übliche Deutung beigelegt.
Die Fläche, welche von der Abscissenachse, der Ordinate an der Bruchgrenze und der
durch die Bruchgrenze gehenden letzten Belastungslinie eingeschlossen wird, ist nach
Vorigem als Maſs der Arbeit anzusehen, welche auf die gesammte elastische Formänderung des Versuchsstückes verwendet wurde, und
es drückt demzufolge die Differenz der ganzen Diagrammfläche und dieser Fläche die
Arbeit aus, welche die bleibende Formänderung des Stückes erforderte. Beide
Arbeitsgröſsen, bezogen auf die Gewichtseinheit (1g), geben daher die Arbeitsmodel Ae und Ab für elastische und bleibende Formänderung des
Probestückes an. Ihre Summe ist gleich dem Gesammtarbeitsmodul A.
Wie durch einfache Zugkräfte eine Erhöhung der Elasticitätsgrenze eintritt, so ist
dies auch und zwar in erhöhtem Maſse der Fall, wenn zu der Zugkraft noch eine den
Körper verdichtende Druckkraft hinzutritt. Die Zunahme der Härte, Sprödigkeit und
Elasticität des Drahtes bei dem Durchlaufen der Ziehlöcher ist allgemein bekannt und
wird durch die im Folgenden bemerkten weiteren Versuche mit Phosphorbronzedraht von
neuem bestätigt.
Der für den zuletzt besprochenen Versuch benutzte Draht wurde durch Glühen wieder
erweicht und hierauf in 7 Passagen von 0,67 auf 0mm,42 Dicke ausgezogen. Die hierzu aufgewendete mechanische Arbeit betrug
speciellen Messungen zu Folge etwa 22mk für 1g Draht. Das bei der Belastung des Drahtes bis zum
Eintritt des Bruches erhaltene Diagramm zeigt Fig. 2. Auch
hier wurden während des Versuches mehrere Entlastungen vorgenommen. Vor allem wird,
gegenüber dem vorigen Versuch, die beobachtete geringe Bruchdehnung auffallen, die
hier nur δ = 42mm
oder Z = (42 × 100) : 5575 = 0,753 Procent der
Anfangslänge (l = 5m,575) betrug, während dieselbe bei dem ausgeglühten Draht zu 55,3 Proc. im
Durchschnitt gefunden wurde. Die Elasticitätscurve EG
Tabelle I. Phosphorbronzedraht.
Textabbildung Bd. 245, S. 72
Bezeichnung der Proben; Geglühter
Draht; Hartgezogener Draht; Arbeit für 1g =; Mittel aus 1 bis 5; Mittel aus 6,
7; Mittel aus 8, 9, 10; Anfangslänge 1 mm; Anfangsdicke dmm; Querschnitt fqmm;
Gewicht der Probe gg; Länge für 1g λmm; Belastung an Elasticitätsgrenze;
Bruchbelastung; Tragmodul; in km Drahtlänge 1; Elasticitätsmodul; in km
Drahtlänge 2; Bruchmodul auf 1qmm; Dehnungen an der Elasticitätsgrenze Δ; in
Millimeter; „ Bruchth. von l; „ Proc. von l; „ Proc. von δ; Gesammtdehnung an
der Bruchgrenze δ; in Millimeter; in % v. l, Z =; 55,34; Elastische Dehnung an
der Bruchgrenze δ e in Procent von δ; Bleibende Dehnung an der Bruchgrenze δ b
in Procent von δ; Arbeitsmodul 5; Diagrammcharakteristik 6 η; Elasticitätsgrad
ε; Bildsamkeitsgrad B
Anmerkungen zu Tabelle I.
1 Länge eines Drahtstückes, dessen Gewicht die
Beanspruchung eines Drahtes von gleichem Einheitsgewicht (Gewicht für die Länge 1)
bis zur Elasticitätsgrenze bewirken würde.
2 Länge eines Drahtstückes, dessen Gewicht einen
Draht von gleichem Einheitsgewicht um seine Anfangslänge vollkommen elastisch zu
strecken vermöchte. (Längenmodul genannt in Dr. Bohn's
Ergebnisse physikalischer Forschung. Leipzig 1878.
W. Engelmann.)
3 Länge eines Drahtes, welcher senkrecht
herabhängend, durch sein Eigengewicht abreiſsen würde.
4 Mittelwerth aus den Versuchen 2, 3 und 4.
5 Zum Zerreiſsen von 1g Draht aufzuwendende mechanische Arbeit.
6 Verhältnis der Diagrammfläche zu der durch
Bruchdehnung und Bruchbelastung bestimmten Rechteckfläche. Dasselbe gibt ein
allgemeines Bild des Diagrammes. Für eine den Dehnungen proportionale Zunahme der
Belastungen ist die Diagrammfläche ein Dreieck, daher η
= 0,5. Ist η > 0,5, so wendet die Diagrammcurve der
Abscissenachse die concave, ist η < 0,5, die
convexe Seite zu.
schneidet die Diagrammcurve an der die Belastung p' = 6250g
anzeigenden Stelle und theilt im Anschluſs an die Diagrammcurve die Fläche OPQ in zwei Theile Fe und Fb, deren Gröſsenverhältniſs von demjenigen der
gleichen Flächen bei dem vorigen Versuch schon nach dem Augenschein wesentlich
verschieden ist; die Ausmessung liefert: e = Fe : Fb = 36 und, da ferner Tl = 5km,05 beträgt, so folgt B = Z : εTl = 0,004. Durch
das Ziehen ist somit, gegenüber dem geglühten Draht, die Zähigkeit um (55,3 – 0,753)
100 : 55,3 = 98,6 Proc. vermindert, dafür das elastische Verhalten etwa auf das 2600
fache gesteigert worden.
Analoge Ergebnisse lieferte ein dritter Versuch mit einem 757mm langen Phosphorbronzedraht, welcher vom
geglühten Zustand ausgehend ohne ferneres Glühen in 16 Durchzügen von 1mm,02 Anfangsdicke auf 0mm,42 Enddicke unter einem Arbeitsaufwand von etwa
51mk für 1g
Draht ausgezogen wurde. Es fand sich:
Z= 1,4 Proc., ε = 16, Tl = 6km,43, B = 0,014.
Die Herabminderung der Zähigkeit geht mit einer Erhöhung der Festigkeit Hand in Hand.
Sowohl der Tragmodul, als der Bruchmodul wird erhöht. Während beim:
ausgeglühten Draht.
Tl = 1,37km
P = 33k/qmm
betrug, fand sich beim:
schwach gezogenen Draht
T1 =
5,05
P = 62,0
stark gezogenen Draht
Tl =
6,43
P = 97,2
Gegenüber den Erfahrungen, welche von anderen Beobachtern bei der Untersuchung von
Kupfer und Kupferlegirungen im geglühten und bearbeiteten Zustand gewonnen
wurdenVgl. Weisbach; Ingenieur- und Maschinenmechanik,
4. Auflage. Bd. 1 S. 369. Mousson: Die Physik,
Bd. 1. Allgemeine und Molecularphysik S.
203., muſs die Abnahme des Elasticitätsmoduls bei Steigerung des
allgemeinen elastischen Verhaltens der Versuchsstücke auffallen. Derselbe stellte
sich für die drei betrachteten Drahtsorten zu:
E = 11647k, E = 10904k, E = 8780k auf 1qmm
heraus. Diese Abnahme ist durch die beobachteten
Dehnungsverhältnisse an der Elasticitätsgrenze bedingt. Diese letztere, durch Procent der Anfangslänge
ausgedrückt, trat bei folgenden Streckungen ein:
Δ = 0,109 Proc. Δ = 0,413 Proc. Δ = 0,594
Proc.
Eine vollständige Uebersicht über sämmtliche gewonnenen Versuchswerthe enthält
vorstehende Tabelle I. Dieselbe zeigt deutlich, welchen beträchtlichen Einfluſs die
Bearbeitung auf die Festigkeitseigenschaften der Phosphorbronze hat und wie unsicher
und unstatthaft daher der Vergleich von Versuchsresultaten dann ist, wenn nicht
gleichzeitig die Herstellung der Versuchsstücke mit in Betracht gezogen wird. Durch
Verdünnung des Drahtes auf etwa 0,4 der anfänglichen Dicke wächst die zum Zerreiſsen
erforderliche Kraft auf das dreifache und es steht auſser Zweifel, daſs diese
Bruchbelastung bei demselben Draht durch dessen weitere Verdichtung auf dem Drahtzug
ohne zwischeninne erfolgendes Ausglühen auch noch weiter steigerungsfähig ist. Bei
Telephonleitungen kommt es im Allgemeinen weniger auf groſse Biegfähigkeit des
Drahtes an; dagegen ist eine groſse Festigkeit erwünscht, um mit möglichst dünnen
Drähten möglichst groſse Entfernungen überspannen zu können. Es wird daher mit
Rücksicht auf Haltbarkeit und geringes Einsenken des frei gespannten Drahtes
zweckmäſsig sein, möglichst hart gezogenen Draht zu verwenden, vorausgesetzt, daſs
die Leitungsfälligkeit hierdurch nicht beeinträchtigt wird.
Im Anschluſs an diese Betrachtungen sind in Tabelle II noch die Ergebnisse der
Untersuchung von ausgeglühtem Silicium-Kupferdraht der Firma Lazare Weiller mitgetheilt, welche erkennen lassen, daſs dieses Metall in
seinen Festigkeitseigenschaften der Phosphorbronze namentlich in Bezug auf
Dehnbarkeit nachstellt, daſs es aber immerhin als ein festes und zähes Metall zu
bezeichnen ist:
Tabelle II. Geglühter Silicium-Kupferdraht.
Bezeichnung der Probe
1
2
3
4
5
Mittelaus1 bis 5
Anfangslänge lmm
106
183
185
230
258
–
Anfangsdicke dmm
0,96
0,85
0,85
0,85
0,85
–
Querschnitt fqmm
0,724
0,567
0,567
0,567
0,567
–
Gewicht der Probe gg
0,675
0,934
0,950
1,192
1,326
–
Bruchbelastung pg
20500
16500
16800
16900
16750
–
Bruchmodul für 1qmm; Pk
28,3
29,1
29,6
29,8
29,5
29,3
Reiſslänge Rkm
3,29
3,23
3,27
3,26
3,27
3,26
Gesammtdehnung an Bruchgrenze
in Millim. δ =in % von l; Z =
28,426,8
48,526,5
4524,3
6427,8
7629,5
–27,0
Elastische Dehnung an der Bruch- grenze δe in % von δ
–
–
–
0,6
0,8
0,7
Bleibende Dehnung an der Bruch- grenze δb in % von δ
–
–
–
99,4
99,2
99,3
Arbeitsmodul Amk
0,695
0,718
0,655
0,765
0,814
0,729
Diagrammcharakteristik η
0,813
0,831
0,818
0,837
0,847
0,829
Anhang. Zur Ermittelung der auf das Ziehen des Drahtes
verwendeten mechanischen Arbeit fand ebenfalls der Zerreiſsapparat von Reusch Anwendung. Der zu ziehende Draht wurde, nachdem
er bereits ein Stück durch das betreffende Loch des Zieheisens von Hand geführt war,
in der Klemme des Apparates eingespannt und vollends durch das Ziehloch gezogen. Die
hierfür erforderliche Federspannung, die anfänglich stieg, dann bei dem Beginn der
Drahtbewegung rasch um einen kleinen Betrag sank, im Uebrigen aber nahezu constant
blieb, wurde durch das gleichzeitig aufgenommene Diagramm angezeigt. Dieselbe fand
sich für die einzelnen Ziehlöcher, deren Verdünnungsfaktor zwischen 0,852 und 0,982
schwankte und im Mittel 0,914 betrug, in Folge dieser Verschiedenheit und der
verschiedenen Glätte der Ziehlöcher ebenfalls sehr verschieden.
Die nahezu constante Gröſse der Zugkraft innerhalb eines jeden Versuches gestattet,
die für die Erzeugung von 1m Draht erforderliche
mechanische Arbeit L1mk direkt anzugeben. Aus dem Gewicht
gg von 1m des gezogenen Drahtes folgt dann die für das
Ausziehen von 1g Draht in einem Ziehloch
erforderliche mechanische Arbeit zu L == L1
: g. Bei einer Verdünnung des Drahtes von 1,02 auf 0mm,42, die in 14 Durchgängen erfolgte, schwankte
L zwischen 1 und 6mk und betrug im Mittel 3mk,2. Auf
analoge Weise wurde die Reibung des Drahtes im Ziehloch annähernd bestimmt, indem
die Kraft zum Durchziehen des vorher von Hand zweimal durch das gleiche Ziehloch
geführten Drahtes ermittelt wurde. Hiernach beträgt die zur Ueberwindung der Reibung
des Drahtes im Ziehloch nothwendige mechanische Arbeit für 1g Draht im Mittel etwa 24 Procent der gesammten
für das Durchziehen aufgewendeten Arbeit. Die sekundliche Zuggeschwindigkeit betrug
während der Versuche etwa 3mm.
Fig.
4 gibt als Beispiel die Diagramme wieder, welche bei dem Ziehen von 1mm,02 starkem geglühtem, bezieh. 0mm,74 starkem bereits hartgezogenem
Phosphorbronzedraht erhalten wurden. Für ersteres gelten folgende Werthe:
Verdünnungsfaktor
= 0,970
Länge des Drahtes nach dem Durchgang des Ziehloches
= 169mm
Gewicht des Draht Stückes
= 1g,16
Gewicht für 1m Draht
= 6g,87
Mittlere Gesammtzugkraft
= 6k,75
Mittlere Zugkraft zur Ueberwindung der Reibung
= 2k,00
Mechanische Arbeit zur Erzeugung von 1m Drahtlänge
= 6mk,75
Arbeit zur Ueberwindung der Reibung für 1m Drahtlänge
= 2mk,00
Arbeit zur Erzeugung von 1g
Draht
= 0mk,983
Reibungsarbeit bezogen auf 1g Draht
= 0mk,291
Antheil der Reibungsarbeit an der Gesammtarbeit
= 29,7 Proc.
Tafeln