| Titel: | Ellipsograph von L. Bigge in Köln. |
| Autor: | H–s. |
| Fundstelle: | Band 245, Jahrgang 1882, S. 253 |
| Download: | XML |
Ellipsograph von L. Bigge in Köln.
Mit Abbildungen auf Tafel 19.
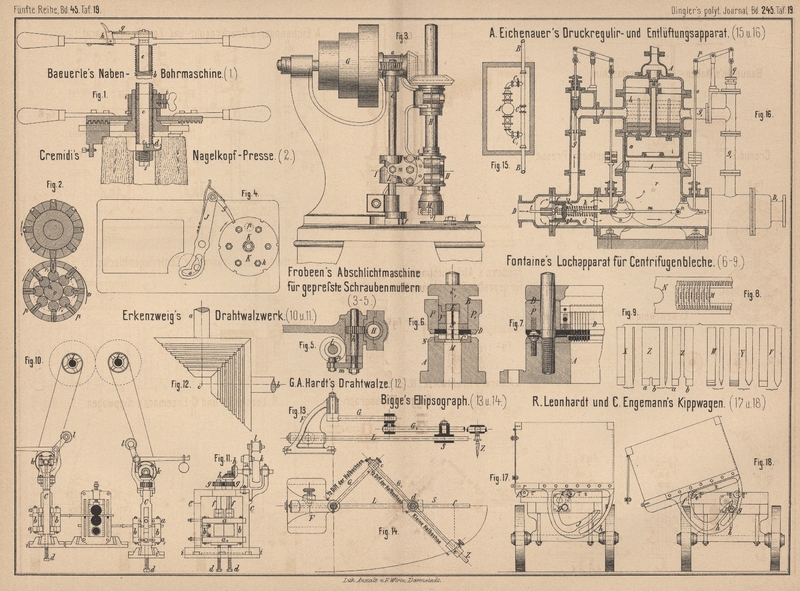
Bigge's Ellipsograph.
Die ziemlich groſse Zahl der verschiedenen, mit wenig Berechtigung als
„Zirkel“ bezeichneten Ellipsographen wurde von L.
Bigge in Köln abermals vermehrt. Wie aus Fig. 13 und
14 Taf. 19 ersichtlich, besteht das neue, sehr einfache InstrumentVgl. Delabar 1877 223
* 461. 224 347. Thallmayer 1878 227 337 592. Schmeißer 1880 236 *
288. Klinkerfues 1881 242 * 413. aus einem Fuſs F mit darin befestigter Leitschiene L und
zwei mit einander verbundenen Gelenkstangen G, G1 wovon die kürzere G
mit ihrem einen Ende um einen im Fuſs F gelagerten
Zapfen schwingt, während die längere Stange G1 mit einem beiläufig in ihrer Mitte angebrachten
Auge einen Zapfen umfaſst, welcher von dem auf der Leitschiene L gleitenden Schieber S
getragen wird. Verschiebt man den letzteren längs der Leitschiene, so beschreibt der
nahe dem Ende der Stange G1 befestigte Schreibstift Z eine Ellipse,
deren kleine Halbachse gleich der Entfernung ed des
Schreibstiftes vom Zapfen am Schieber S ist, während
die einander gleichen Gelenklängen oc und cd der halben Differenz der Halbachsen
gleichkommen.
Bezeichnen wir mit:
a und b die groſse bezieh. kleine Halbachse der Ellipse,
m die veränderliche Länge od,
n die Projection df der kleinen Halbachse de auf die Richtung od,
y den senkrechten Abstand ef des Punktes e von of,
so ist \overline{c\,d}=\frac{1}{2}\ (a-b)
und wegen Aehnlichkeit der Dreiecke n : b = m : (a – b)
Setzen wir nun:
\overline{o\,f}=x=m+n=n\,\left(\frac{a-b}{b}+1\right)=\frac{n\,a}{b}
so erhalten wir, da n2
= b2
– y2 ist:
\frac{x^2\,y^2}{a^2}=b^2-y^2 oder
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1,
die bekannte Mittelpunktsgleichung der Ellipse.
H–s.
Tafeln