| Titel: | Ueber Deutung und Genauigkeit von Festigkeitsdiagrammen; von Prof. Hugo Fischer. |
| Autor: | Hugo Fischer |
| Fundstelle: | Band 251, Jahrgang 1884, S. 337 |
| Download: | XML |
Ueber Deutung und Genauigkeit von
Festigkeitsdiagrammen; von Prof. Hugo
Fischer.
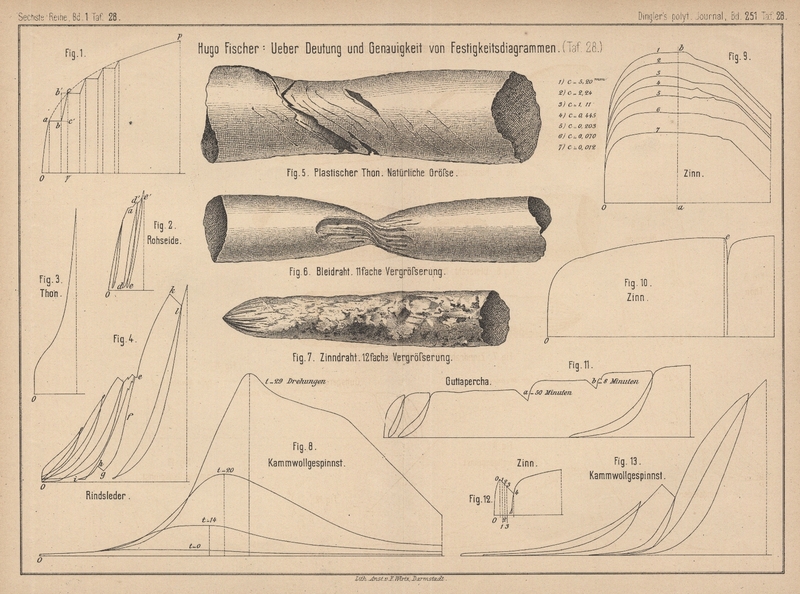
Mit Abbildungen auf Tafel 28.
Hugo Fischer, über Festigkeitsdiagramme.
Bei der experimentellen Untersuchung fester Körper auf ihre Festigkeitseigenschaften
kommen stets zwei Faktoren direkt zur Erhebung: Die Gröſse der auf den Körper
wirkenden Kraft und die Formänderung, welche der Körper unter der Wirkung dieser
Kraft in der Kraftrichtung erleidet. Hierbei entspricht bei stofflich gleichartigen
Körpern einer bestimmten Gröſse der Kraft (Beanspruchung) stets eine bestimmt groſse
Deformation. Durch Verknüpfung dieser beiden Faktoren mit Hilfe eines rechtwinkligen
Coordinatensystemes geht das Festigkeitsdiagramm hervor. Die Ermittelung beider
Gröſsen in jedem Augenblicke der Beanspruchungsdauer erfolgt am zweckmäſsigsten,
weil am genauesten und raschesten, mit Hilfe der selbstzeichnenden
Festigkeitsmesser.
Die Diagramme lassen mit Leichtigkeit die den wachsenden Belastungen entsprechenden
Längenänderungen des Versuchsstückes, die dem Bruche desselben entsprechenden Werthe
der Spannung und Längenänderung erkennen, sie geben Aufschluſs über die Gröſse der
von der spannenden Kraft während der Versuchsdauer verrichteten mechanischen Arbeit
und liefern bei weiterer Ausbildung ein Mittel, das elastische Verhalten des
betreffenden, der Untersuchung unterworfenen Materials genauer zu studiren. Form und
Gröſse des Diagrammes ist daher im Allgemeinen als ein bildlicher Ausdruck
derjenigen Eigenschaften eines Materials zu betrachten, welche bei der Beanspruchung
eines aus diesem hergestellten Versuchsstückes durch mechanische Kräfte in Frage
kommen: der Festigkeit, Elasticität und Zähigkeit.
Der Vergleich der Diagramme verschiedener Materialien läſst sofort die groſse
Mannigfaltigkeit in dem Auftreten der betreffenden Eigenschaften erkennen, da sich
die Diagramme sowohl durch die Gestalt der Diagrammcurve, als die Gröſse der von
dieser, der Endordinate und der Abscissenachse umschlossenen Fläche unterscheiden.
Während erstere von dem Verhältnisse der jeweiligen Kraft- und Dehnungswerthe
abhängen, ist letztere durch die absolute Gröſse dieser beiden bedingt.
Wird die Belastung des Probestückes noch vor dem Bruche unterbrochen, so verwickeln
sich die Erscheinungen und demgemäſs auch die Gestalt der Diagramme wesentlich und
es treten neue Momente hervor. Bei der stetigen Entlastung des bis zu einem gewissen
Grade angespannten Versuchsstückes erfolgt die Begrenzung des Diagrammes stets durch
eine gegen die Abscissenachse geneigte Curve derart, daſs deren Durchschnittspunkt
mit dieser Achse zwischen dem Fuſspunkte der letzten Diagrammordinate und dem
Coordinatenanfange liegt. Dieser Schnittpunkt theilt die gröſste Diagrammabscisse
daher in zwei Theile. Der Theil, welcher an die Endordinate grenzt, stellt die Gröſse derjenigen
Formänderung dar, welche das Probestück in Folge seiner Elasticität in der Richtung
der beanspruchenden Kräfte erfahren hat; der andere Theil gibt die dem Stücke
mitgetheilte bleibende Formänderung an. Das Verhältniſs dieser beiden Strecken führt
daher das elastische Verhalten des Versuchskörpers vor Augen. Bei einer auf die
Entlastung folgenden Neubelastung des Stückes steigt die neue Belastungslinie im
Allgemeinen neben der Entlastungslinie empor und schneidet dieselbe entweder in
demjenigen Punkte der Diagrammcurve, in welcher die Belastung unterbrochen wurde,
oder noch vor Erreichen desselben. Nur unter bestimmten Verhältnissen fallt die
Entlastungs- und Belastungscurve zusammen.
Um zu einer Erklärung dieser hier kurz geschilderten, im weiteren Verlaufe dieser
Arbeit ausführlicher zu besprechenden Erscheinungen zu gelangen, ist es
erforderlich, ein Bild von der allgemeinen Constitution der Festkörper zu entwerfen.
Es wird zweckmäſsig sein, hierbei derjenigen Entwickelung zu folgen, welche aus
wahrnehmbaren Vorgängen bei der Beanspruchung dieser Körper durch äuſsere Kräfte
entspringt, um somit rückwärts in ihr die Erklärung für die verwickelteren Vorgänge
zu suchen.
Wird einem Körper eine bleibende Formänderung ertheilt, so findet, wie sich in vielen
Fällen leicht beobachten läſst, eine Umordnung der kleinsten, diesen Körper
zusammensetzenden Theile, der Körperelemente, statt. Dieser Umordnung setzt sich im
Inneren des Körpers ein Widerstand entgegen, dessen Ueberwindung eine äuſsere
(mechanische) Kraft von bestimmter Gröſse erfordert. Diese Kraft kann umgekehrt als
Maſs für diesen inneren Widerstand betrachtet werden. Da dieser Widerstand in seiner
Erscheinung und seiner Folgewirkung mit den bei dem Aneinandergleiten fester Körper
zur Beobachtung kommenden Erscheinungen übereinstimmt, pflegt man denselben die innere Reibung1) Vgl. Dr. P. Schmidt; Ueber die innere Reibung
fester Körper. (Breslau 1880. Verlag von A.
Gosohorsky. des Körpers zu nennen.
Die Anerkennung dieser inneren Reibung zwischen den kleinsten Theilen eines
Festkörpers bedingt aber die Annahme, daſs diese kleinsten Theile oder
Körperelemente sich berühren und zwar unter Druck berühren müssen. Von diesem
Drucke, sowie von der Oberflächenbeschaffenheit der Körperelemente hängt die Gröſse
der inneren Reibung eines Körpers ab. Die Entstehung dieses Druckes ist auf das
Vorhandensein von molekularen, zwischen den einzelnen Körperelementen thätigen
Anziehungskräften (Cohäsionskräften) zurückzuführen, welche mit der gegenseitigen
Annäherung der Mittelpunkte zweier benachbarter Elemente wachsen, mit der
Vergröſserung des Abstandes abnehmen.
Diese Annahme führt im weiteren Verfolge der Erscheinungen un- abweisbar zu der Forderung der
Deformirbarkeit und elastischen Beschaffenheit der Körperelemente selbst. Die
Notwendigkeit dieser Voraussetzung tritt am klarsten bei dem Verfolge derjenigen
Erscheinungen hervor, welche sich bei der Beanspruchung der Körper auf Druck
abspielen. Würden die sich berührenden kleinsten Körpertheile vollkommen starr und
unelastisch sein, wie es die neuere Molekularphysik annimmt, so müſsten
Druckbeanspruchungen stets nur bleibende Formänderungen an festen Körpern ergeben.
Diesem widerspricht die Erfahrung vollständig, indem bei dem Zusammendrücken eines
Körpers stets auch eine elastische Formänderung beobachtet werden kann, welche nach
dem Wegfalle der drückenden Kraft wieder vollständig verschwindet.
Auf Grund dieser Betrachtungen werde für die folgenden Untersuchungen, welche sich
nur auf homogene Körper beziehen, angenommen: Ein Festkörper
bestehe aus sehr kleinen, stofflich und räumlich unter sich völlig gleichen,
vollkommen elastischen Körperelementen, deren Gestalt unter dem Einflüsse
äuſserer Kräfte Veränderungsfähig ist. Benachbarte Körperelemente stehen unter
sich in Berührung und werden durch die denselben eigenen molekularen
Anziehungskräfte unter bestimmtem Drucke in dieser erhalten. Die Körperelemente
sind unter gewissen Bedingungen gegen einander verschiebbar und es werden
dieselben nach der Verschiebung durch eine im Körperinneren thätige passive
Kraft (innere Reibung) verhindert, wieder in die am Beginne der Beanspruchung
vorhanden gewesene gegenseitige Stellung zurückzukehren.
Die nachstehenden Ausführungen werden zeigen, wie weit diese Hypothese über die Constitution der festen Körper, die übrigens in ihren
einzelnen Theilen nicht neu ist, zur Erklärung derjenigen Erscheinungen ausreicht,
welche bei der Festigkeitsuntersuchung solcher Körper zur Beobachtung kommen.
Ein Körper zeigt bei seiner Beanspruchung durch mechanische Kräfte so lange nur elastische Formänderungen, als die Grenze der
vollkommenen Elasticität, die sogen. „Elasticitätsgrenze“ noch nicht
überschritten ist, d.h. so lange die beanspruchende Kraft kleiner ist als die innere
Reibung des Körpers. Dem Ueberschreiten dieser Grenze folgt die Ueberwindung dieser
Reibung und damit eine Verschiebung der kleinsten Körpertheile gegeneinander; es
tritt das „Flieſsen“ des Materials ein. Ohne
Aenderung der inneren Pressungen des Körpers müſste dieses Flieſsen bei constanter
oder, im weiteren Verlaufe, wegen der Querschnittsänderung des Versuchskörpers bei
abnehmender Kraft stattfinden; die Diagrammcurve müſste anfänglich parallel zur
Abscissenachse verlaufen. Ein solcher Verlauf ist aber bei Druckbeanspruchung
niemals, bei Zugbeanspruchung nur bei gewissen Materialien annähernd wahrzunehmen.
In allen Fällen findet auch nach dem Eintritte des Flieſsens der Körperelemente ein
stetiges Ansteigen der Curve statt. Dieses Ansteigen ist aber nur durch ein
Anwachsen der inneren Reibung zu erklären. Da die materielle Beschaffenheit des Probestückes
während des Versuches eine Aenderung nicht erfährt und mithin eine Aenderung der
Oberflächenbeschaffenheit der Körperelemente nicht denkbar ist, so kann der Grund
für die Erhöhung der inneren Reibung nur in einer Steigerung des Druckes zwischen
den kleinsten Körpertheilen zu suchen sein. Die, wenn auch sehr kleine, jedoch
immerhin meſsbare Volumen Verminderung bezieh. Dichtigkeitserhöhung homogener Körper
bei Zug- oder Druckbeanspruchung bestätigt diese Ansicht, wenn sie auch die Ursache
der Erscheinung nicht erkennen läſst.
Denkt man sich den Vorgang bei der Beanspruchung eines Körpers durch mechanische
Kräfte nicht stetig verlaufend, so würde das hierbei erhaltene Diagramm eine
treppenförmige Gestalt, wie sie Fig. 1 Taf.
28 zeigt, annehmen. Nach dem Eintritte des Flieſsens bei a setzt sich dieses unter Constanterhaltung der Kraft bis b fort. Hierbei wird im Körper in Folge entstehender
Querdrücke die innere Reibung vergröſsert, so daſs von b an die Ueberwindung derselben eine Vergröſserung der Kraft um einen der
Ordinatenstrecke bb' entsprechenden Werth erforderlich macht.
Diese durch die Zunahme der äuſseren Kraft gemessene Vermehrung der inneren Reibung
bedingt aber für die erneute Herbeiführung einer gegenseitigen Verschiebung der
Körperelemente deren gröſsere Deformation, welche der Voraussetzung zu Folge
elastisch ist und durch die Strecke bc' im Diagramme gemessen wird. Mit anderen
Worten, es muſs der Körper in dem neuen Zustande, den die Diagrammordinate yc charakterisirt, bei einer Neubelastung stärker
belastet werden, um auſser der elastischen Formänderung auch eine bleibende zu
erzeugen; die „Elasticitätsgrenze“ ist höher gelegt worden. In Wirklichkeit
finden diese Vorgänge in jedem Augenblicke der Belastung statt, verlaufen also
stetig, so daſs sich die Erhöhung der Grenze der vollkommenen Elasticität bis zum
höchsten Punkte p der Diagrammcurve fortsetzt.Vgl. H. Fischer: Untersuchungen über das
Verhalten des Phosphorbronzedrahtes bei der Beanspruchung durch Zugkräfte,
1882 245 * 70.Praktische Anwendung findet die Erhöhung der Elasticitätsgrenze u.a. in der
Treibriemenfabrikation und bei dem von Uchatius
(vgl. 1875 217 * 122. 1877 223 242) angegebenen Verfahren zur Herstellung von
Bronzegeschützen. Im ersteren Falle bezweckt eine bis nahe an die
Bruchgrenze des Leders fortgesetzte Reckung die Verminderung des Längens der
Riemen während des Gebrauches, also Verkleinerung der bleibenden Dehnung; im
letzteren Falle wird durch Druck die Verdichtung und damit Steigerung der
Festigkeit der inneren Wandung des Geschützrohres erzielt.
Die Annahme, daſs das Ansteigen der Diagrammcurve während des Versuches in der That
auf eine Vergröſserung der inneren Reibung durch Druckvermehrung zwischen den
kleinsten Körpertheilen zurückzuführen sein dürfte, wird durch die zu beobachtenden
Aenderungen der Materialbeschaffenheit, nämlich Erhöhung der Dichte, Festigkeit,
Elasticität und Härte des Materials bei dem Ziehen und Walzen der Metalle zu Draht
und Blech, dem Drehen der Gespinnstfäden u. dgl. sehr wahrscheinlich gemacht. Eine indirekte
Bestätigung dürfte in dem Zäherwerden und der Verminderung des elastischen Verhaltens verschiedener Materialien durch
entsprechende Erwärmung zu finden sein. Durch diese wird eine Ausdehnung der Körper,
also eine gegenseitige Entfernung der Mittelpunkte der Körperelemente und damit
Verminderung der Cohäsion und der inneren Reibung herbeigeführt.
Mit der Steigerung der streckenden Kraft und der daraus hervorgehenden Zunahme der
inneren Reibung geht in Folge des Aneinandergleitens der kleinsten Theile eine
Querschnittsverminderung des Versuchskörpers Hand in Hand. Durch diese wird die Zahl
der Reibungsstellen, also auch die Reibung selbst allmählich verkleinert. Bei
Zugbeanspruchung wird die Zugkraft allmählich langsamer wachsen als die Streckung
und die Diagrammcurve wird sich daher mehr und mehr einer zur Abscissenachse
parallelen Lage nähern und diese Lage erreichen, wenn der Quotient:
\frac{\mbox{Zunahme der inneren Reibung durch
Druckvermehrung}}{\mbox{Abnahme der inneren Reibung durch
Querschnittsverminderung}}=1
geworden. Dieser Quotient kleiner wie 1 bedeutet dagegen eine
Abnahme der inneren Reibung, also zur Erhaltung des Gleichgewichtszustandes auch
eine Verminderung der Zugkraft. Die Diagrammcurve sinkt und nähert sich, der
Reibungsabnahme entsprechend, stetig der Abscissenachse. Die Curve besitzt also
einen Culminationspunkt, dessen Ordinate die gröſste von dem Versuchsstücke zu
tragende Belastung angibt.
Diesen Vorgang veranschaulichen deutlich die in Fig. 8 und
9 Taf. 28 dargestellten, bei dem Zerreiſsen von kammwollenen Streckbändern bezieh. von Zinndraht auf dem Festigkeitsmesser von D.
Reusch (1880 235 * 414) erhaltenen Diagramme.
Die Curve dieser Diagramme hat einen deutlich sichtbaren Culminationspunkt, über
welchen hinaus sich dieselbe mehr und mehr senkend, noch weiter fortsetzt. Die
Erreichung des Punktes ist bei den Metalldrähten mit einer deutlich wahrnehmbaren
Aenderung der Oberfläche des Versuchsstückes verbunden. Dieselbe wird rissig und
diese Risse breiten sich unter gleichzeitiger Vertiefung mehr und mehr aus, je
weiter die Belastung fortschreitet. In Folge der Unvollkommenheit aller Versuchskörper in Bezug auf Gestalt, Homogenität
und Stoffgleichheit ist diese Ausbreitung ungleichförmig; sie vertheilt sich nicht
über das Stück gleichmäſsig, sondern wirft sich bald auf diejenigen Stellen, welche
dem idealen Zustande am wenigsten entsprechen; es treten örtliche Contractionen ein
und schlieſslich kommt es an einer Stelle zum Bruche. Besonders deutlich ist dieser
Vorgang an Drähten aus reinem Zinn und Blei sowie an Stäben aus plastischem Thone wahrzunehmen (vgl. Fig. 5, 6
bezieh. 7 Taf. 28).
Diese Querschnittscontractionen des Versuchsstückes verschwinden entweder nach dem
Bruche wieder mehr oder weniger, oder sie bleiben auch nach dem Bruche deutlich an
den Bruchenden erkennbar. Letzteres ist namentlich bei zähen, wenig elastischen
Körpern, wie Zinn, Blei, plastischer Thon u. dgl. der Fall; ersteres bei solchen Körpern, welche sich wie
Glas, Stahl, Kautschuk, Guttapercha u.a. durch ein besonders starkes elastisches
Verhalten auszeichnen. Während durch Glühen erweichte Silberdrähte eine deutlich
sichtbare Contraction der Bruchenden zeigen, verschwindet diese bei hartgezogenem
Drahte mit Zunahme der Elasticität und Sprödigkeit mehr und mehr. Interessant sind
die in Fig. 5 und 6 sichtbaren
Verwerfungen der Bruchflächen, welche auf das Auftreten von Scherkräften auch bei
reiner Zugbeanspruchung hindeuten dürften.
Die Erreichung des Culminationspunktes der Diagrammcurve ist nur bei wenig Körpern zu
beobachten. Die gröſste Näherung zeigen gewöhnlich die Diagramme schwach elastischer
Materialien. In den meisten Fällen erfolgt der Bruch des Versuchsstückes viel früher
und zwar, mit wenig Ausnahmen, um so eher, je elastischer das Material ist. Die
Ursache hierzu ist vielleicht in der Ueberwindung der in der Längenrichtung des
Versuchsstückes wirkenden molekularen Anziehungskräfte im gefährlichen Querschnitte
zu suchen.
Zur Beobachtung der angedeuteten Verhältnisse eignen sich besonders die bei
Zugbeanspruchung langer Versuchsstücke erhaltenen Diagramme, da bei diesen der
Einfluſs der Einspannstellen fast verschwindet. Hierauf deutet das seltene Vorkommen
des Bruches an der Einspannstelle hin. Bei Druckbeanspruchungen tritt dagegen dieser
Einfluſs in Folge der stets geringen Länge des Probestückes und der während des
Versuches bald eintretenden Vergröſserung der Druckflächen so stark hervor, daſs die
Druckcurve schon nach verhältnifmäſsig geringer Zusammenpressung des Probestückes
einen Wendepunkt zeigt und sich rasch von der
Abscissenachse entfernt. Diese Erscheinung, auf welche auch Kick (vgl. 1882 244 * 36) bereits aufmerksam
gemacht, zeigt das in Fig. 3 Taf.
28 dargestellte, bei dem Zerdrücken eines Cylinders aus plastischem Thone auf dem
Rensch'schen Apparate erhaltene Diagramm.
Die Abweichungen in der Gestalt der Festigkeitsdiagramme materiell verschiedener
Versuchskörper sind wahrscheinlich auf Unterschiede in der Gröſse der den
Körperelementen eigenen elastischen Kraft, der die innere Reibung bedingenden
gegenseitigen Pressung und Oberflächenbeschaffenheit dieser Elemente, sowie der Art
und Geschwindigkeit der Fortpflanzung der Zug- und Druckspannungen im Inneren des
Versuchskörpers zurückzuführen. Daſs auf letztere die Gestalt der kleinsten
Körpertheile von Einfluſs, dürfte kaum zweifelhaft sein.
Diese im Vorstehenden der Betrachtung und Deutung der Festigkeitsdiagramme zu Grunde
gelegte ideale Constitution der Körper, stellt der Bau der textilen Gespinnste gewissermaſsen bildlich dar. Das einfache, nur aus
parallel zu einander angeordneten Elementarfasern gebildete Streckband kann als
Repräsentant eines homogenen, stabförmigen Körpers dienen, in welchem durch
geeignete Arbeitsverfahren, z.B. bei Metalldrähten durch Ausglühen, die inneren
Spannungen auf ein Minimum herabgedrückt sind. Die Fasern selbst sind stark elastisch
und nur schwach an einander gedrückt; sie haften durch Reibung an einander (innere
Reibung), welche ihrer gegenseitigen Verschiebung einen gewissen Widerstand
entgegensetzt. Durch Zusammendrehen werden die gegenseitigen Abstände der
Einzelfasern verkleinert, die Pressung und damit die Reibung zwischen den Fasern
erhöht. Der Widerstand, welcher sich einer Verschiebung derselben entgegenstellt,
wird vermehrt. Von solchen verschieden stark gedrehten Gespinnsten genommene
Zerreiſsungsdiagramme zeigen demnach das Anwachsen der Bruchbelastung mit der durch
stärkere Zwirnung hervorgerufenen Zunahme der inneren Reibung. Bei schwacher Drehung
des Fadens, so lange derselbe also noch ein lockeres Gefüge zeigt und die inneren
Spannungen in Folge dessen noch gering sind, besitzen die Diagrammcurven, ebenso wie
diejenigen weicher Metalle (Zinn, Blei u. dgl.), einen ziemlich sicher bestimmbaren
Culminationspunkt. Mit zunehmender Zwirnung steigt die Curve rascher empor und endet
dann noch vor Erreichung des Culminationspunktes. Die in Fig. 8 Taf.
28 gezeichneten Diagramme, welche bei der Belastung von Kammwollgespinnsten mit t = 0, 14, 20 bez. 29 Drehungen auf 1m Länge erhalten wurden, geben ein deutliches Bild
dieses Verhaltens; sie zeigen zugleich, daſs dasselbe genau demjenigen entspricht,
welches bei der Beanspruchung homogener Körper, wie durch Ziehen verdichteten und
gehärteten Metalldrähten, beobachtet wird.
(Schluſs folgt.)
Tafeln