| Titel: | Ueber Deutung und Genauigkeit von Festigkeitsdiagrammen; von Prof. Hugo Fischer. |
| Autor: | Hugo Fischer |
| Fundstelle: | Band 251, Jahrgang 1884, S. 385 |
| Download: | XML |
Ueber Deutung und Genauigkeit von
Festigkeitsdiagrammen; von Prof. Hugo
Fischer.
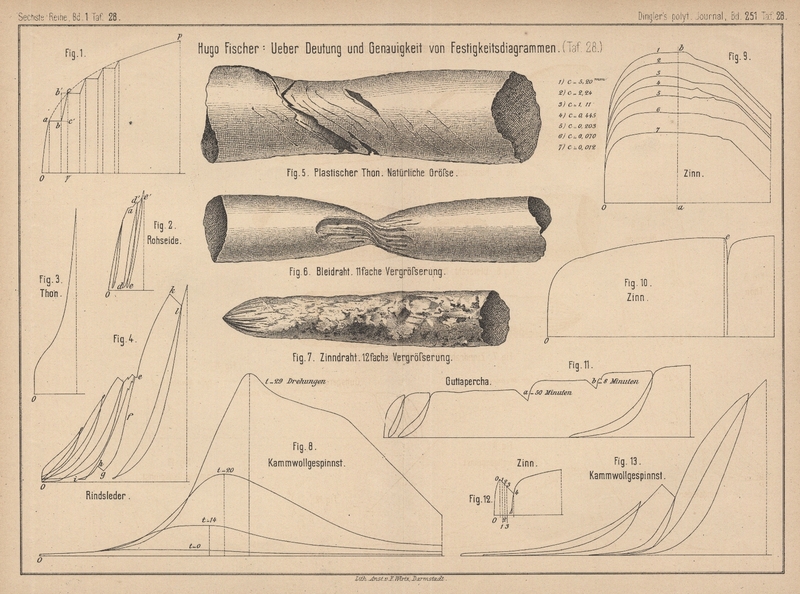
Mit Abbildungen auf Tafel 28.
(Schluſs der Abhandlung von S. 337 d.
Bd.)
Hugo Fischer, über Festigkeitsdiagramme.
Die Gröſse der Kraft und mechanischen Arbeit, welche zur Ueberwindung der inneren
Reibung eines Körpers erforderlich ist, nimmt zu: 1) mit der
Gröſse der inneren Reibung; 2) mit der
Geschwindigkeit, mit welcher diese Reibung überwunden wird, also das
Verschieben (die Beschleunigung) der Körperelemente
erfolgt. Hiernach muſs ein auf Zug beanspruchter Körper, bei rascher aber
stetiger (nicht stoſsweiser) Beanspruchung eine gröſsere Festigkeit zeigen, als ein
langsam belasteter, in welchem die Körperelemente nur ganz allmählich ihre
gegenseitige Lage ändern. Diese Voraussetzung wird durch Versuche bestätigt.
Die Fig. 9 Taf. 28 stellt eine Reihe von Diagrammen dar, welche bei dem
Zerreiſsen von 1mm,6 dicken Zinndrähten (Feinheitsnummer oder Meter auf
1^g\frakfamily{N}=0,068) auf dem Apparate von Reusch erhalten wurden. Die Länge der Probestücke war
nahezu gleich; sie schwankte zwischen 55 und 61mm.
Die Beanspruchung der einzelnen Drähte erfolgte mit verschiedener Geschwindigkeit,
deren Gröſse durch Beobachtung derjenigen Zeit bestimmt wurde, welche für die
Erreichung einer Dehnung um die Strecke Oa
aufgewendet wurde. Diese Versuchsdauer betrug für die einzelnen Proben:
Nr.
1
2
3
4
5
6
7
Zeit in Secunden
15
33
65
155
315
840
4405.
Es entsprechen diese Zeitwerthe annähernd der Erreichung des
Culminationspunktes in den einzelnen Diagrammcurven. Nach dem Ueberschreiten der
Grenzordinate ab wurden die Stücke bei nahezu
gleicher Geschwindigkeit zum Bruche geführt.
Nach diesen Zeitwerthen und der zwischen O und ab liegenden Länge der Diagrammcurven berechnen
sich die bezüglichen secundlichen Geschwindigkeiten c
des Schreibstiftes in Millimeter für:
Nr. 1
2
3
4
5
6
7
c = 5,20
2,24
1,11
0,445
0,203
0,070
0,012.
Ein Blick auf die Figur 9
zeigt deutlich den Einfluſs dieser Zuggeschwindigkeiten auf die Festigkeit des
Materials. Während bei Versuch Nr. 7 bereits bei einer Belastung von p = 2700g die Curve
ihren Culminationspunkt erreicht, ist bei dem mit einer etwa 450 mal gröſseren
Geschwindigkeit ausgeführten Versuche Nr. 1 die Tragkraft auf p = 5100g, also etwa
das Doppelte, gestiegen. Für die einzelnen Versuche berechnen sich die den
Belastungen p entsprechenden Reiſslängen
R=p\,\frakfamily{N}^{km}, wie folgt:
Nr. 1
2
3
4
5
6
7
R = 0,371
0,347
0,316
0,292
0,272
0,231
0,184.
Diese Verschiedenheit der gröſsten Diagrammordinaten bedingt
auch bei nahe gleicher Gröſse der einzelnen diesen Ordinaten entsprechenden
Dehnungen der Versuchsstücke Unterschiede in den für die Streckung aufgewendeten
Arbeitsgröſsen A. Es betragen dieselben auf 1g des Materialgewichtes bezogen und in
Meterkilogramm ausgedrückt, bei:
Nr. 1
2
3
4
5
6
7
A = 0,130
0,109
0,085
0,082
0,083
0,090
0,067,
schwanken also bei den Versuchen Nr. 1 und 7 ebenfalls um etwa
den 2 fachen Betrag.
Dagegen ist die allgemeine Gestalt der Diagramme nur wenig veränderlich, was die
Einzelwerthe der diese charakterisirenden Zerreiſsungs- oder Völligkeitsquotienten
bezeugen; es beträgt nämlich dieser Völligkeitsquotient η für:
Nr. 1
2
3
4
5
6
7
η = 0,850
0,856
0,832
0,863
0,828
0,853
0,804.
Diese Beobachtungen lassen sich mit gleichem Erfolge an verschiedenen anderen Körpern
wiederholen. Die Ergebnisse derselben sind für die Festigkeitsprüfung der
Materialien wohl zu beachten, da sie zeigen, wie leicht auf Grund unzweckmäſsig
angestellter Versuche bezüglich der Haltbarkeit der Materialien Fehlschlüsse gezogen
werden können. Zum Glücke sind diejenigen Materialien, welche vorzugsweise bei
technischen Constructionen Anwendung finden, meist solche, bei denen die gewöhnlich
bei der Untersuchung übliche Belastungsgeschwindigkeit für zulässig zu bezeichnen
ist. Dies gilt namentlich von den als Baumaterialien
verwendeten Metallen; dagegen wird Vorsicht bei der Prüfung von Hölzern, Seilen u.
dgl. geboten sein. Vielleicht dürften solche Fälle, wo Constructionstheile, welche,
auf eine bestimmte Tragfähigkeit geprüft, bald danach unter geringerer Belastung
zerstört wurden, zuweilen mit den geschilderten Erscheinungen in Verbindung zu
bringen sein.
Die beträchtlichen Abweichungen dieser bei verschieden rascher Beanspruchung eines
und desselben Materials erhaltenen Versuchsergebnisse legt die Frage nach der für
die Anstellung eines Versuches zweckmäſsigsten
Geschwindigkeit nahe. Die Beantwortung dieser Frage kann natürlich nicht allgemein
erfolgen; sie wird sich jederzeit auf ein bestimmtes Material beziehen müssen. Der
allein richtige Weg zur Beantwortung ist das Experiment und die Anwendung geeigneter
Versuchsapparate. Als solche sind die selbstzeichnenden
Festigkeitsmesser mit Federbelastung zu bezeichnen, da diese Belastungsart
leicht und sicher ein Uebermaſs der Beanspruchung, also auch das Ueberschreiten der
zulässigen Belastungsgeschwindigkeit erkennen läſst. Der Vortheil der Federbelastung
gegenüber jeder anderen Belastungsart liegt in dem selbstthätigen Anpassen der
Belastungsgröſse an die in dem Versuchsstücke herrschende Spannung und dem Wegfalle
von Trägheitswirkungen, wie sie bei Gewichtsbelastung leicht auftreten.
Wird ein Material zu rasch und dem zu Folge auch zu stark belastet, so äuſsert sich
die in demselben angehäufte überschüssige Energie durch Fortsetzung der Streckung
auch dann, wenn eine Zunahme der Belastung nicht mehr stattfindet. In Folge dieser
Streckung wird die gespannte Feder allmählich entlastet, bis der
Gleichgewichtszustand zwischen Federspannung und der Spannung des Versuchskörpers
eingetreten. Dies gibt sich deutlich durch Senken der Diagrammcurve kund. Die
Entlastung erfolgt anfangs rasch, in der Folge langsamer und langsamer. Fig.
12 Taf. 28 zeigt in der Strecke Oo den
Anfang eines bei rascher Belastung von Zinndraht erhaltenen Diagrammes. Die Linie
o-4 ist die durch freiwillige Entlastung des unter
der Federspannung erhaltenen Versuchsstückes entstandene Entlastungslinie. Die
Stationen geben die Entlastungsgröſse nach bestimmten Zeitintervallen an. Es
entspricht:
der Strecke
o-1
o-2
o-3
o-4
eine Zeitdauer von
12
40
100
1090 Minuten.
Die analoge Erscheinung, bei der Untersuchung von Guttapercha beobachtet, zeigt das Diagramm Fig.
11 Taf. 28; die beiden Entlastungsstationen a
und b entsprechen einer Entlastungsdauer von 50 bezieh.
8 Minuten.
Bewirkt man die Entlastung eines zu rasch belasteten
Probestückes durch direkt herbeigeführte Verminderung der Federspannung, wie dies
bei der Bestimmung des elastischen und bleibenden Theiles der Formänderung üblich
ist, so zieht sich dasselbe in Folge seiner elastischen Beschaffenheit zusammen.
Diesem Zusammenziehen wirkt aber die Energie der in der Streckrichtung in Bewegung
befindlichen Massentheilchen entgegen, so daſs die Entlastungscurve durch diese
Massenwirkung eine Aenderung ihrer Gestalt erfährt. Diese Ablenkung kann so
bedeutend werden, daſs die elastische Streckung des Materials für die Beobachtung
nicht nur gänzlich verschwindet, sondern die Streckung am Ende der Entlastung sogar
gröſser erscheint, als die Streckung an deren Beginne. Das in Fig. 10
Taf. 28 dargestellte, für Zinn geltende Diagramm zeigt
deutlich diesen Fehler; die Entlastungscurve schneidet auſserhalb des Fuſspunktes
der den Entlastungspunkt e enthaltenden Ordinate die
Abscissenachse. Die elastische Dehnung ist nicht meſsbar, obgleich sie an dieser
Stelle des Diagrammes etwa 0mm,3 betragen würde.
Gleiches Vorkommen wird auch bei der Untersuchung von plastischem Thone
beobachtet.
Versuchsstücke, welche sich nach erfolgter vollständiger Entlastung unter der Wirkung
der inneren Elasticitätskräfte noch fernerweit zusammenziehen, liefern bei der
allgemein üblichen Belastungsgeschwindigkeit nie Diagramme, die zur Bestimmung der
elastischen und bleibenden Formänderungen ohne weiteres brauchbar sind. Diese
Diagramme sind jederzeit durch den Umstand charakterisirt, daſs bei einer Belastung,
welche sich unmittelbar an die stattgehabte Entlastung anschlieſst, die
Neubelastungslinie
vor dem Entlastungspunkte die Entlastungscurve
schneidet. Hierauf ist bereits von E. Müller im Civilingenieur, 1882 * S. 631 bei Gelegenheit der
Untersuchung von Rohseide aufmerksam gemacht
worden.
Nach dem Angeführten ist der Grund für diese Erscheinung in einer zu raschen und daher nicht
normalen Belastung des Probestückes zu suchen. Derselbe Effect, wie durch
die Zusammenziehung des Materials nach vollständiger Entlastung, wie sie E. Müller angibt, muſs sich bei genügend langsamer
Belastung direkt erreichen lassen, da dann ein Kraftüberschuſs, welcher ein Voreilen
der flieſsenden Theilchen während der Streckung bewirken könnte, nicht vorhanden
ist. Der Versuch bestätigt diese Annahme vollkommen. Als Versuchsmaterial wurde eine
Probe der von E. Müller untersuchten Rohseidenfäden (crins) benutzt, welche den Müller'schen Diagrammen zu Folge die Abweichung der Belastungscurve von
dem Entlastungspunkte deutlich erkennen lassen. Die Belastung; wurde sehr langsam
ausgeführt: das Diagramm Fig. 2 Taf.
28 bestätigt das Gesagte. Die Unterbrechung des stetigen Verlaufes der Diagrammcurve
bei a ist auf einen Wechsel in der
Belastungsgeschwindigkeit zurückzuführen. Auch an anderen Materialien ist diese
Erscheinung deutlich zu beobachten, wie ein Blick auf die in den Figuren 4
und 13 Taf. 28 dargestellten Diagramme von lohgarem Rindsleder und
Kammwollgespinnst lehrt.
Beachtet man, daſs die zu rasche Belastung eines Probestückes für eine bestimmte
Dehnung stets eine gröſsere Spannung ergibt, als sie bei genügend langsamer
Belastung würde erhalten worden sein, so leuchtet ein, daſs alle diejenigen
Diagramme, in denen bei der Bestimmung der elastischen und bleibenden Formänderung
des Materials die im Schnittpunkte der Entlastungscurve mit der Abscissenachse
ansetzende neue Belastungslinie nicht durch den
Entlastungspunkt der Diagrammcurve führt, zu groſse
Werthe der Bruchspannung und des Arbeitsmoduls ergeben müssen. Derartige Diagramme
sind demnach falsch und für die Bestimmung dieser
Werthe nicht brauchbar.
Die Beachtung dieser Thatsache bietet gleichzeitig ein Mittel zur Festsetzung der für
die Untersuchung eines Materials zulässigen
Belastungsgeschwindigkeit. Diese liegt nur dann vor, wenn die neue
Belastungscurve auch den Entlastungspunkt der Diagrammcurve enthält, und kann durch
einen Vorversuch für jedes Material leicht bestimmt werden. Allerdings wird die
Untersuchung vieler Materialien durch Beachtung dieses Umstandes, wenn auch nicht
schwieriger, so doch zeitraubender als bisher, da die zulässige
Belastungsgeschwindigkeit in vielen Fällen sehr klein ist und die Abnahme eines
Diagrammes mehrere Stunden erfordern kann; der jetzt übliche Handbetrieb des
Festigkeitsmessers wird hierbei zweckmäſsig durch Elementarkraftbetrieb ersetzt
werden. Mindestens wird in jedem Falle, wo die Diagramme die geforderte Eigenschaft
nicht zeigen, eine Angabe der Belastungsgeschwindigkeit unerläſslich sein.
Dieser im Vorhergehenden erwiesene Einfluſs der Geschwindigkeit auf die Gestalt und
Lage der Diagrammcurve gestattet auch noch weitere Schlüsse über die Entstehung
jener eigentümlichen Schleifen zu ziehen, welche das Diagramm vieler Materialien bei
Ent- und Neubelastung des Versuchsstückes aufweist und die u.a. auch in den Figuren
2, 4, 11 bezieh. 13 deutlich
zu sehen sind. Auffällig ist, daſs dieselben vorzugsweise an solchen Versuchsstücken
zur Darstellung gelangen, welche dem Organismenreiche entstammen, während Metalle
z.B. dieselben weniger stark ausgeprägt bezieh. gar nicht zeigen. Es lag nahe, die
Entstehung dieser Schleifen als Folge einer zu groſsen Entlastungsgeschwindigkeit zu
betrachten, da bei dieser die Körperelemente nicht mit genügender Schnelligkeit der
Wirkung der inneren Elasticitätskräfte zu folgen vermögen. Zum Theile wurde diese
Ansicht durch den Versuch bestätigt, indem die Breite der bei sehr langsamer
Entlastung erhaltenen Schleife ee1 im Rohseiden-Diagramme (Fig. 2)
sichtlich geringer ist als diejenige, welche die bei der Entlastung dd1 erhaltene
Schleife aufweist. Dies ist ein Vorkommniſs, das sonst nie beobachtet wird; die folgenden Schleifen nehmen vielmehr stets nicht
nur an Flächengröſse, sondern auch an Breite zu. Zum Verschwinden konnte dieselbe
jedoch nicht gebracht werden.
Ein ähnliches Ergebniſs lieferte ein mit lohgarem Rindsleder angestellter Versuch.
Nachdem in einer 2 stündigen Pause von dem Schreibstifte in dem Punkte e (Fig. 4) die
normale Höhenlage der Diagrammcurve erreicht war, wurde die Entlastung in 90 Minuten
von e bis f ausgeführt.
Der Verlauf der Linie ef lieſs, verglichen mit
der Entlastungscurve der vorhergehenden Schleife, erkennen, daſs durch diese
langsame Entlastung ein Verschwinden der Schleife nicht herbeigeführt werden konnte.
Die Lage des Punktes f änderte sich auch nicht während
einer 24 stündigen Ruhepause. Nach Ablauf derselben fand die weitere Entlastung rasch statt, wobei die erhaltene Linie fg steiler abfällt als die Strecke ef, ein Umstand, welcher den wenn auch geringen
Einfluſs der Entlastungsgeschwindigkeit auf die Gestalt und Lage der
Entlastungscurve erkennen läſst. An die Erreichung des Punktes g, dem eine nur geringe Spannung der Apparatfeder
entspricht, schloſs sich abermals eine 48 stündige Ruhepause. In dieser zeigte sich
schon nach Verlauf von 24 Stunden der bereits bei f
erwartete Vorgang. Die inneren Elasticitatskräfte des Materials kamen zur Wirkung
und verursachten nicht nur eine Verkürzung des Probestückes, sondern, da dasselbe
noch mit der schwach gespannten Apparatfeder in Verbindung stand, auch eine
Neubelastung dieser bis zur Herbeiführung des Gleichgewichtszustandes. Die
Curvenstrecke gh gibt ein deutliches Bild von
diesem Vorgange. Der Endpunkt h liegt dicht neben der
neuen, von i ausgehenden Belastungslinie; er würde
wahrscheinlich auf derselben liegen, wenn die Neubelastung genügend langsam
vorgenommen worden wäre.
Daſs dies nicht der Fall gewesen, zeigt die Wellengestalt des oberen Theiles dieser
Linie, welche durch in die Belastung eingeschaltete kurze Ruhepausen entstanden ist.
Ueber e hinaus fand die Belastung rasch statt, daher
von k bis l die Senkung
der Curve während 90 Minuten Pause bis zur Erreichung der normalen Höhenlage.
Obgleich durch diese Versuche das Verschwinden der Entlastungsschleifen und damit des
Zusammenfallens der Entlastungscurve mit der neuen Belastungscurve nicht direkt
herbeigeführt werden konnte, so scheinen die Beobachtungen meine Erwartung bezüglich
dieses Zusammenfallens dennoch indirekt zu bestätigen. Daſs die erhoffte
Neubelastung der Apparatfeder durch die Wirkung der inneren Kräfte des Materials
nicht bereits bei f eintrat, sondern sich erst nach
erfolgter gröſserer Entspannung der Feder bei g merkbar
machte, dürfte nach meinem Dafürhalten auf die Verschiedenheit der elastischen Kraft
des Materials der Feder und derjenigen des Versuchsstückes zurückzuführen sein. Die
elastische Kraft der Feder ist gröſser als die des Leders und deshalb vermochte
letztere die erstere nicht zu überwinden, so lange die Feder eine groſse Spannung
besaſs. Erst dann, als durch theilweise Entlastung die Elasticität der Feder
geschwächt war, kamen die Elasticitätskräfte des Versuchsstückes zur Geltung und
vermochten die Federkraft zu besiegen. Je mehr sich die Versuchsmaterialien in ihrem
elastischen Verhalten demjenigen der zur Belastung benutzten Feder nähern, um so
kleiner werden die Entlastungsschleifen werden, bis sie schlieſslich bei völliger
Gleichheit und entsprechend langsam ausgeführter Ent- und Belastung ganz
verschwinden. Das Material der Apparatfedern ist gewöhnlich Stahl; die härteren
Metalle, welche in ihrem elastischen Verhalten gegenseitig die geringsten
Abweichungen zeigen, liefern in der That die kleinsten Schleifen; bei Eisen und
geglühtem Stahle sind dieselben kaum bemerkbar. Drähte aus weichen und zähen
Metallen liefern um so kleinere Schleifen, je stärker sie durch Ziehen verdichtet,
gehärtet und elastischer werden, so daſs sie sich in ihren Eigenschaften dem
gehärteten Stahle mehr und mehr nähern.
Die Genauigkeit der Diagramme wird durch das Vorhandensein der Entlastungsschleifen
nicht beeinträchtigt, sobald nur die Belastung des Probestückes mit einer solchen
Geschwindigkeit erfolgt, daſs die Linie, welche bei der auf eine Entlastung
unmittelbar folgenden Neubelastung erhalten wird, durch den Entlastungspunkt der
Diagrammcurve führt.
Diese hier ausführlich geschilderten Vorgänge sind in ihrer Erscheinung identisch mit
der zuerst von Wilhelm Weber beobachteten
Längenänderung eines Seidenfadens nach erfolgter Be-
bezieh. Entlastung. W. WeberPoggendorff's Annalen, 1835 S. 247. 1841 S. 1 ff. Vgl. auch Dietzel: Ueber das Gesetz des Gleichgewichtes
starrer elastischer Körper im Civilingenieur,
1856 S. 144 ff. nennt diesen Vorgang die elastische Nachwirkung
des Versuchskörpers und
erklärt ihn durch die Annahme, daſs die elastische Formänderung der Moleküle stets
eine bestimmte, zuweilen sehr lange Zeit erfordert. Er
hat beobachtet, daſs diese Aenderung im Anfange dieser Zeit rascher stattfindet als
gegen das Ende hin, so daſs der Zusammenhang zwischen der Zeit und den Dehnungs-
oder Verkürzungswerthen durch eine Curve dargestellt wird, welche, vom
Coordinatenanfange rasch steigend, der Abscissenachse ihre concave Seite zuwendet
und im weiteren Verfolge vielleicht asymptotisch zu einer der Abscissenachse
parallelen Geraden verläuft. Derselbe Beobachter hat ferner gefunden, daſs diese
elastische Nachwirkung besonders auffallend bei Versuchskörpern vegetabilischen oder
animalischen Ursprunges auftritt, während sie sich bei Metallen häufig der
Beobachtung gänzlich entzieht. Er findet die Erklärung für diese Erscheinung in dem
verschieden elastischen Verhalten dieser Körper, indem die Metalle wohl eine groſse
elastische Kraft gegenüber den organisirten Körpern besitzen, diese Kraft sich
jedoch bei sehr geringer Aenderung der Länge des Versuchsstückes äuſsert.
Nach den im Obigen zur Darstellung gelangten Ergebnissen der Versuche über den
Einfluſs der Belastungsgeschwindigkeit auf die Gröſse der Belastung, die mit den
Erfahrungen W. Weber's völlig übereinstimmen, dürfte es
wohl kaum zweifelhaft sein, daſs die von Weber
„elastische Nachwirkung“ genannte Erscheinung nicht allein in dem elastischen
Verhalten der Körperelemente gesucht werden darf, sondern auch als eine Function der
Belastungsgeschwindigkeit und der inneren Reibung betrachtet werden muſs. Gröſsere
Belastungsgeschwindigkeit liefert für gleiche Dehnung des Versuchsstückes dann, wenn
eine weitere Vergröſserung der Belastung nicht mehr stattfindet, stets auch eine
gröſsere Nachstreckung in Folge der gröſseren, in dem Versuchsstücke angesammelten
Energie, wie dies die Versuche beweisen. Die gegenseitige Verschiebung der
Körperelemente wird hierdurch noch längere Zeit unterhalten und die Geschwindigkeit
dieser Verschiebung nimmt mit Abnahme der Energie ebenfalls ab. Vermag sich hierbei
die spannende Kraft der durch die Geschwindigkeitsverminderung allmählich
abnehmenden inneren Reibung anzupassen, wie dies bei Federbelastung oder der von Weber angewendeten indirekten Gewichtsbelastung der
Fall ist, so tritt schlieſslich ein Gleichgewichtszustand zwischen den inneren und
äuſseren Kräften ein. Bleibt dagegen die äuſsere Kraft constant, überwiegt sie also
dauernd den inneren Widerstand des Körpers, so wirkt sie auch auf die Dauer
beschleunigend auf die Körperelemente; die Verschiebung derselben setzt sich fort
und endet schlieſslich mit dem Zerreiſsen des Versuchsstückes. Dieser Vorgang kann
bei direkter Gewichtsbelastung von Gespinnsten leicht beobachtet werden.
Durch sehr rasche Belastung gelingt es, die Trägheit der in Bewegung befindlichen
Körperelemente so weit zu steigern, daſs der von
W. Weber als unmöglich bezeichnete Fall einer Streckung des Versuchsstückes nach erfolgter Entlastung
desselben eintritt, wie dies das Diagramm Fig. 10
deutlich zeigt. Diese Nachstreckung erfolgt anfangs rasch und verzögert sich
allmählich, da der lebendigen Kraft der Körperelemente die elastische Kraft dieser
entgegenwirkt. Nach eingetretenem Gleichgewichtszustande, welcher durch das Ende der
Nachstreckung bezeichnet wird, zieht sich ein jedes Körperelement in Folge der ihm
eigenen Elasticität zusammen und wirkt hierbei beschleunigend auf die ihm
benachbarten Elemente, so daſs diese nach erfolgter elastischer Zusammenziehung
vermöge der in ihnen angesammelten lebendigen Kraft ihren Weg unter Ueberwindung der
inneren Reibung mit verzögerter Geschwindigkeit fortsetzen, bis sie zur Ruhe
gelangen. Von diesem Augenblicke an findet eine weitere Verkürzung des
Versuchsstückes nicht mehr statt, die „elastische Nachwirkung“ ist Null
geworden.
Die von den Körperelementen hierbei aufgenommene lebendige Kraft ist um so gröſser,
je länger die beschleunigende Kraft (Elasticität der Elemente) zu wirken vermag. Bei
den dem Organismenreiche angehörenden Körpern ist aber das Verhältniſs zwischen
elastischer Kraft und elastischer Streckung ein kleineres als bei den Metallen, d.h.
es entspricht bei jenen einer bestimmten Beanspruchung innerhalb der rein
elastischen Formänderung eine gröſsere Streckung als bei diesen. Es ist deshalb
erklärlich, daſs dem Pflanzen- oder Thierreiche entnommene Versuchsstücke eine
beträchtlich gröſsere Formänderung nach stattgefundener
Entlastung zeigen als die Metalle, was den Beobachtungen Webers bezüglich der „elastischen Nachwirkung“ dieser Materialien
vollkommen entspricht.
Auch unter diesen neuen Gesichtspunkten bleibt die von W.
Weber für die Verkürzung eines Versuchsstückes nach erfolgter Entlastung eingeführte Benennung „elastische Nachwirkung“ eine zutreffende, da diese Verkürzung im
ursächlichen Zusammenhange mit der Elasticität des Materials steht; für die
Nachstreckung eines Versuchsstückes nach erfolgter
Belastung dürfte sie dagegen den hierbei stattfindenden, von dem elastischen
Verhalten des Materials unabhängigen Vorgang nicht decken.
Dresden im Januar 1884.
Tafeln