| Titel: | Pickles' Aufwindebewegung für Webstühle. |
| Fundstelle: | Band 252, Jahrgang 1884, S. 319 |
| Download: | XML |
Pickles' Aufwindebewegung für
Webstühle.
Mit Abbildungen auf Tafel 25.
Pickles' Aufwindebewegung für Webstühle.
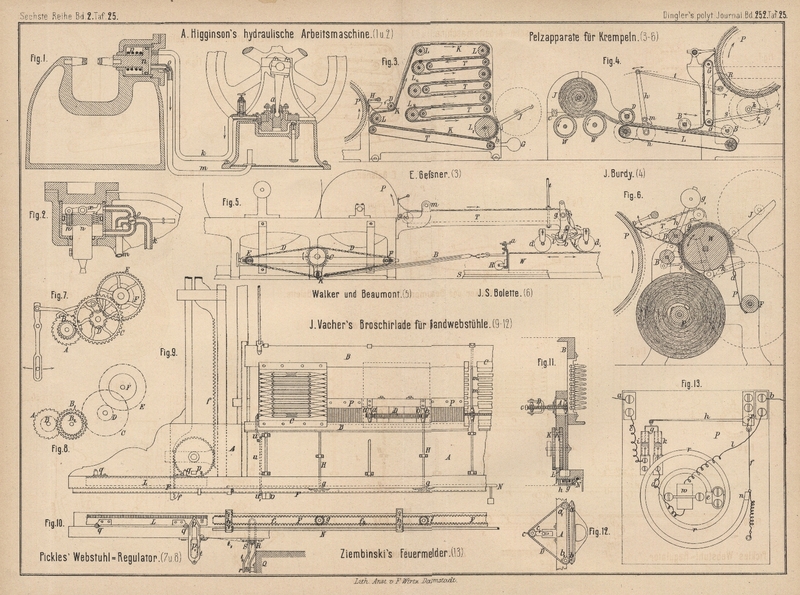
Bei den Webstühlen für Baumwoll- und Kammgarnstoffe erfolgt die Aufwindung des
Gewebes und damit die Bestimmung der Gewebedichte durch eine von der Ladenschwingung
bewegte Klinke, welche ein Klinkenrad A (Fig.
7 Taf. 25) und durch eine doppelte Räderübersetzung B, C und D, E die
Aufwindewalze F dreht. Bei jedem Ladenschlage wird das
Klinkenrad A um einen Zahn bewegt; um daher eine
verschiedene Gewebedichte oder verschiedene Anzahl Schuſs auf die Längeneinheit zu
erlangen, wird das Rad B ausgewechselt. Diese Anordnung
birgt eine groſse Unbestimmtheit, welche sich aus folgender Betrachtung ergibt.
Bezeichnen die Buchstaben A bis E die bezüglichen Zähnezahlen der Räder und F den Umfang der Aufwindewalze, so findet man die
Anzahl Schuſs auf die Längeneinheit zu
n=\frac{(E\,:\,D)\,(C\,:\,B)\,A}{F}=\frac{E\,C\,A\,:\,D\,F}{B}.
Beispielsweise sei A = 50, C = 120, D = 15, E = 75 und der Umfang der Aufwindewalze F
habe 60 Längeneinheiten, dann ist n=\frac{500}{B}.
Wegen der Verkürzung des Gewebes bei seiner Entspannung, wenn es
von dem Webstuhle kommt und welche ungefähr 1,5 Proc. beträgt, muſs um diesen Betrag
die Schuſszahl höher genommen werden, so daſs n=\frac{507}{B}
wird.
Nach dieser Formel ergeben sich für verschiedene Werthe von B, also beim Aufstecken von Wechselrädern folgende
Schuſszahlen auf die Längeneinheit:
Bei
einem
Wechselrade
mit
15
Zähnen
B
= 33,8
„
„
„
„
16
„
„
= 31,687
„
„
„
„
30
„
„
= 16,9
„
„
„
„
31
„
„
= 16,355
„
„
„
„
48
„
„
= 10,562
„
„
„
„
49
„
„
= 10,347.
Es findet also bei der Steigerung des Wechselrades um einen Zahn
eine sehr verschiedene Verminderung der Schuſszahl auf die Längeneinheit statt. Bei
dem Wechselrade von 15 Zähnen beträgt diese rund 2⅕, bei 30 Zähnen ½ und bei 48
Zähnen kaum ¼ Schuſs. Ist z.B. ein Gewebe mit 26 Schuſs in der Längeneinheit
herzustellen, so gibt das 20 zähnige Wechselrad weniger als 25½ Schuſs und das
19zähnige mehr als 26½ Schuſs. Es gibt bei den angenommenen Gröſsen nur ein Rad,
welches die Schuſszahl in runder Ziffer liefert, nämlich das 39zähnige.
Die regelmäſsige Verminderung oder Steigerung der Schuſszahl beim Aendern des
Wechselrades um einen Zahn ist erreicht durch die Anordnung der Aufwindebewegung von
O. Pickles und Comp. in Burnley (vgl. Textile Manufacturer, 1883 S. 539). Wie die Anordnung
in Fig. 8 Taf. 25 zeigt, ist nur ein Doppelrad B1, B2 zwischen die Räder B und C eingeschaltet. Das
Rad B, welches nicht mehr das Wechselrad zur
Schuſszahlbestimmung ist, jedoch gewechselt wird, greift in das nunmehr für die
Aenderung der Schuſszahl bestimmte Wechselrad B1 und das mit letzterem verbundene Rad ist ein
bleibender Trieb für das Rad C Die Gröſse der Räder A und B wird so bestimmt,
daſs, wenn das Klinkenrad A bei jedem Schusse um einen
Zahn vorschreitet, das Rad B1 um 1, 2, 3
oder 4 Zähne bewegt wird. Ist B1 mit Rücksicht auf die Schuſszahl der Längeneinheit
zu 60 angenommen, so erhalten wir, wenn bei jedem Schusse z.B. 3 Zähne desselben
fortgerückt werden, für eine Umdrehung dieses Rades 60 : 3 = 20 Schuſs. Würde ein
Rad mit 61 Zähnen aufgesteckt, so gibt dieses für eine Umdrehung 61 : 3 = 20⅓ Schuſs
und entsprechend ein Rad mit 59 Zähnen 19⅔ Schuſs, also bei Steigerung oder
Minderung des Wechselrades um einen Zahn jedesmal eine Aenderung der Schuſszahl um
eine bestimmte Gröſse = ⅓. Das Verhältniſs der Räder B1, C, D und
E kann so bestimmt werden, daſs für eine Umdrehung
von B2 der Aufwindebaum
F genau die Längeneinheit, z.B. 10cm, aufwindet, so daſs die vorher gefundenen
Zahlen 19⅔, 20 und 20⅓ gleich die Schuſszahlen auf 10cm angeben. Soll nun z.B. ein Gewebe mit 17⅔ Schuſs auf 10cm hergestellt werden, so erhält das erforderliche
Wechselrad, wenn B : A =
3, also für jeden Schuſs 3 Zähne desselben bewegt werden, 17⅔ = 53/3, d. s. 53
Zähne. In derselben Weise tritt die stets gleichbleibende Aenderung der Schuſszahl
ein, nur entsprechend um 1, ½ oder ¼ Schuſs, je nachdem B : A = 1, 2 oder 4 ist. Man hat nun
verschiedene Wechselräder für B, welche entsprechend
angesteckt werden, wenn die sich durch dieselben ergebende Differenz in den
Schuſszahlen bei der Aenderung des Wechselrades B1 um einen Zahn gewünscht wird. (Vgl. Sagar 1880 238 * 470.)
Tafeln