| Titel: | G. B. Grant's Kegelschnittzeichner. |
| Fundstelle: | Band 262, Jahrgang 1886, S. 518 |
| Download: | XML |
G. B. Grant's Kegelschnittzeichner.
Mit Abbildung auf Tafel
32.
Grant's Kegelschnittzeichner.
Dieses von G. B. Grant in Boston angegebene und
„conischer Zirkel“ genannte Instrument soll, wie der ähnliche
Kegelschnittzeichner von Oldenburger (vgl. 1885 255 * 271), alle vier Kegelschnitte, also Kreis, Ellipse,
Parabel und Hyperbel zu zeichnen gestatten.
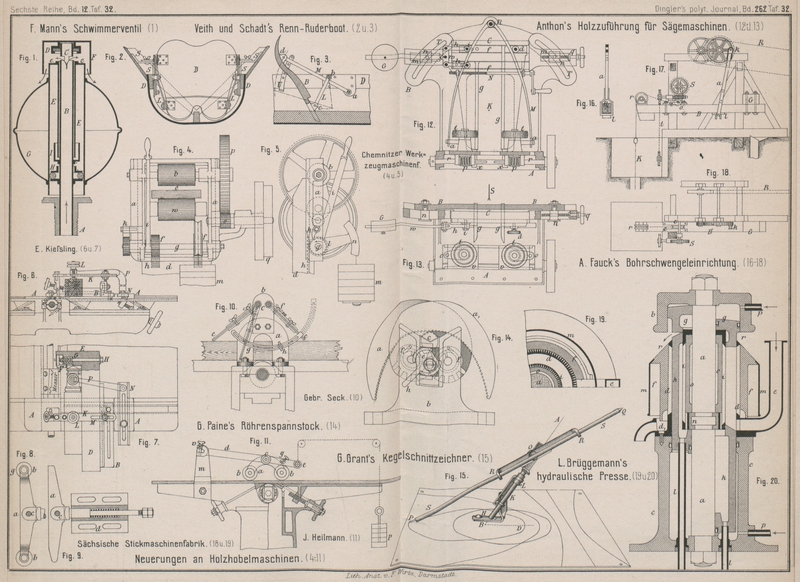
Ein Bleistift PQ (Fig. 15 Taf. 32) ist so
angeordnet, daſs derselbe die Erzeugende eines Kegels bildet, dessen Spitze bei O liegt. Die untergelegte Papierfläche vertritt die
Stelle der schneidenden Ebene und die von dem Bleistifte P gezogene Linie ist die verlangte Kegelschnittscurve. Der Fuſs H des Instrumentes enthält einen Träger, welchem man
eine beliebige Neigung gegen die Papierfläche geben kann. In diesem Träger ist eine
Achse K frei drehbar gelagert, deren Verschiebung in
der Längsrichtung jedoch durch den Hals L gehindert
wird. Ein zweiter mit der Verlängerung von K gelenkig
verbundener Träger R kann unter einem beliebigen Winkel
zur Achse AB festgestellt werden. In diesem Träger
gleitet der Bleistifthalter S.
Beim Gebrauche des Zirkels dreht man die Achse K, wobei
die Bleistiftspitze P auf der Papierfläche eine Linie
beschreibt. Diese Curve nun ist eine Ellipse, wenn der
Winkel OBD gröſser als der Winkel BOP an der Spitze, eine Parabel, wenn der Winkel OBD = BOP, eine Hyperbel, wenn der Winkel OBD kleiner als BOP, endlich ein Kreis, wenn der Winkel OBD
= 90° ist. Selbstverständlich müssen, wenn das Instrument seinen Zweck erfüllen
soll, alle Theile desselben sorgfältig gearbeitet und genau zusammengesetzt sein;
die Linien AB und PQ
müssen sich schneiden und die Theile S und K frei und ohne Erschütterung der bewegenden Kraft
nachgeben.
Tafeln