| Titel: | Donat Bánki's Umdrehungs-Kraftmesser. |
| Fundstelle: | Band 269, Jahrgang 1888, S. 148 |
| Download: | XML |
Donat Bánki's Umdrehungs-Kraftmesser.
Mit Abbildung auf Tafel
9.
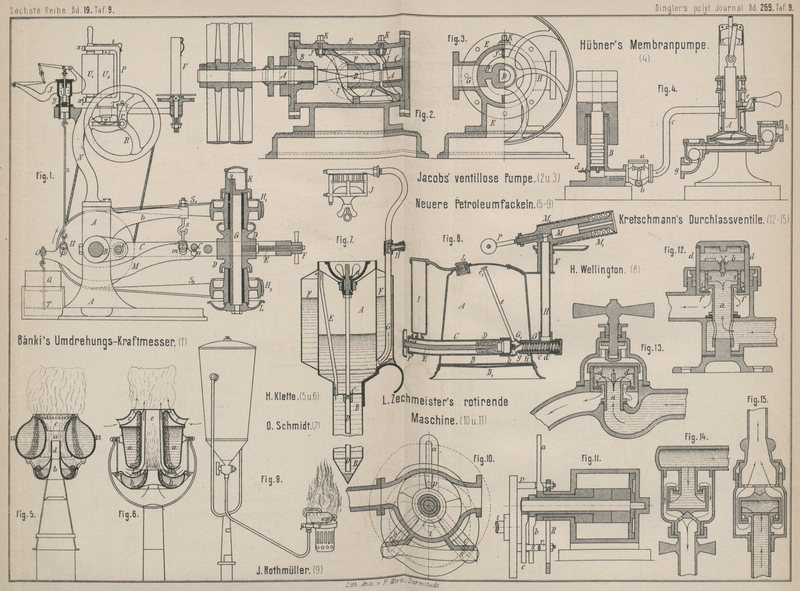
Bánki's Umdrehungs-Kraftmesser.
Das Centralblatt für Elektrotechnik gibt in Nr. 4 vom
Jahre 1888 die Abbildung und Theorie des Umdrehungs-Kraftmessers von Donat Bánki, welcher von Ganz
und Comp. in Ofen gebaut wird und bereits mehrfach ausgeführt und
angewendet ist.
Die bisher gebräuchlichen Einschalt-Kraftmesser, insbesondere auch das so bekannte
Dynamometer von Hartig, haben den Fehler einer gewissen
Unempfindlichkeit in Folge nicht unbeträchtlicher Reibungen, welche z.B. Hartig für seinen Apparat auf etwa 12 Proc. angibt.
Diese Reibungen sind dabei auch nicht einmal unveränderlich, sondern von
verschiedenen Einflüssen – Schmiermittel, Zustand der Radzähne, Riemenspannung
u.s.w. – abhängig, so daſs dieselben ein nicht unbeträchtliches Element der
Unsicherheit in die Beobachtungen einführen, dem Instrumente eine gewisse
Unempfindlichkeit verleihen, kurz – die Resultate wesentlich ungünstig beeinflussen.
Dazu kommt, daſs bei dem Hartig'schen Kraftmesser die
Benutzung sehr hoher Umdrehungszahlen, wie z.B. bei Dynamomaschinen vorhanden, der
Verzahnungen wegen unthunlich erscheint.
Alle diese Umstände bewirken, daſs das Einschalt-Dynamometer noch lange nicht in dem
Umfange in Anwendung steht, welchen es seiner Wichtigkeit wegen wohl verdienen
würde; Bestrebungen auf Verbesserung desselben haben also noch ein dankbares Feld
vor sich.
Das von Ganz und Comp. in Ofen gebaute
Rotations-Dynamometer (Patent Donat Bánki) scheint in
vieler Beziehung ein glücklicher Griff zu sein. Es arbeitet nur mit Riemenscheiben,
wodurch sehr hohe Geschwindigkeiten ohne Nachtheil anwendbar erscheinen, und die
Nebenhindernisse haben auf die Ergebnisse fast keinen Einfluſs, so daſs die
Diagramme keinerlei besonderer Correction bedürfen; endlich ist die Empfindlichkeit
des Instrumentes eine verhältniſsmäſsig sehr groſse, da der Gewichtshebel desselben
sich in Schneiden bewegt, während bei den üblichen Kraftmessern, z.B. dem Hartig'schen, dieser Hebel auf einer dicken Welle
gelagert ist.
Fig. 1 Taf. 9
zeigt den Apparat in senkrechtem Durchschnitte. Derselbe besteht in einem Ständer
A, in welchem die Achse B fest gelagert ist. Auf ihr drehen sich lose aufgesteckt die beiden
Doppelriemscheiben I und II. Ueber diese Scheiben, und zwar über die beiden inneren
Läufe derselben, ist unter Zuhilfenahme zweier Leitrollen H1 und H2 ein Riemen S1
S2 gelegt. Die beiden
Leitrollen sind mit senkrechter Achse derart gegen I und II angeordnet, daſs die
Mittellinien der vier Riemenstücke zu einander parallel laufen.
Das System der Leitrollen ist mit dem Hebelarme C um die
Spitzen c leicht beweglich und die Achse G der Leitrollen in dem Kreuzkopfe D befestigt, der mittels des Schraubenbolzens E und mit der Mutter F
verschoben werden kann, um dadurch den Uebertragsriemen anzuspannen oder zu lockern.
Die Oelbüchse K sorgt für stetige Schmierung der
Leitrollen, der Teller L nimmt das abflieſsende Oel
auf.
Der Hebel C ruht mit allen daran hängenden Theilen auf
der Schneide n des in m an
den Arm b bezieh. Haken s
aufgehängten Wagehebels M auf. Ein Gegengewicht Q im Punkte 0 des
letzteren angreifend, wirkt an einem Hebelarme m0 und
mit einer Uebersetzung \frac{m_0}{m_n} dem Gewichte des Systemes
entgegen, ist jedoch um etwas gröſser, als zum Ausbalanciren nothwendig wäre. Dieses
Mehrgewicht nimmt die Feder y des Indicators J auf, mit welcher der Waghebel durch die Stange z im Punkte p verbunden
ist. Mit dem Gegengewichte ist noch bei T der Kolben
eines „Moderators“ verbunden.
Der Registrirapparat ist auf dem Ständer N befestigt.
Der Papierstreifen wird von einer Walze V abgewickelt,
zwischen den Walzen U1
und U2, welche mit den
Schrauben x und x1 gegen einander gepreſst Werden, durchgezogen und
auf eine zweite hinter der Walze V liegende nieder
aufgewickelt; das Diagramm zeichnet der Indicatorbleistift, der in Fig. 1 Taf. 9 beiseite
gedreht gezeichnet ist, auf die Walze U1 auf. Die Bewegung der Walze U2 erfolgt durch die
Schnecke Z und eine Schraube, welch letztere durch eine
der Schnurscheiben R ohne Uebersetzung von der Scheibe
I oder II aus
angetrieben wird. Der Rahmen P, in welchem die Walzen
untergebracht sind, ist zur Walzenachse excentrisch im Ständer N gelagert, so daſs durch Verdrehen des Rahmens das
Schneckenrad Z mit der Schraube r in oder auſser Eingriff gebracht Werden kann. Die Schneckenradachse
dient gleichzeitig für den Umdrehungszähler
t, und zur Erleichterung der Rechnung hat das
Schneckenrad 100 Zähne erhalten. Auſserdem ist fest an dem Ständer ein hier nicht
gezeichneter Bleistift angeordnet, welcher während des langsamen Abwickelns des
Papier Streifens auf letzteren die Nulllinie aufzeichnet.
Um die Wirkungsweise des Apparates zu verstehen, denke man sich die eine der
Scheiben, z.B. I, von der Transmission aus in der Richtung von rechts nach links
angetrieben. Die Drehbewegung dieser Scheibe überträgt der Riemen S1
S2 auf die Scheibe II, welche durch einen Riemen mit der zu messenden
Arbeitsmaschine verbunden ist. Die Spannungen in den Riemenstücken, welche im
Ruhezustande einander gleich sind, ändern sich während der Bewegung. Bei der
Bewegung im Sinne der Pfeilrichtung sind die oberen Riemenstücke gespannt, die
unteren hingegen schlaff.
Wenn die Führungsrollen keine Widerstände hätten, und das Umbiegen des Riemens keine
Arbeit erfordern würde, müſste S1
= S1
' und S2 = S2
' sein. In der That ist aber S1 um etwas gröſser als S1
' und S2
' gröſser als S2.
Die Summe der Kräfte S1
und S1
' wirken mit dem Momentenarme gleich dem Halbmesser der
Riemenscheiben S = S1 (im Riemenmittel gemessen) auf die Verdrehung des
Hebels C um dessen Drehachse c. Die Kräfte S2 und S2
' wirken zwar mit gleichem Momentenarme, aber sie haben
die Tendenz, den Hebel C in entgegengesetztem Sinne zu
verdrehen.
Das resultirende Moment ist:
[(S_1+{S_1}')-(S_2+{S_2}')]\,R;
wo R den Halbmesser der
Riemenscheiben bezeichnet.
Es läſst sich beweisen, daſs
S_1+{S_1}'-(S_2+{S_2}')=2\,K,
wenn K die Umfangskraft der, die
Arbeitsmaschine treibenden, Scheiben bedeutet. Diese wichtige Eigenschaft wird bei
dem beschriebenen Dynamometer für die ganz genaue Messung der übertragenen
Umfangskräfte benutzt.
Bei einer Uebertragung der Umfangskraft K1 wird ein Theil des Gegengewichtes Q frei und belastet die Feder J des Indicators mit einer Zugkraft von:
\frac{2\,R\,\overline{M\,n}}{\overline{c\,n}+\overline{m\,p}}\,.\,K=\alpha\,K;
α ist eine durch die
Uebersetzungsverhältnisse ein für allemal gegebene Constante. Die mit der
Umfangskraft proportionalen Durchbiegungen der Feder zeichnet der Indicator auf dem
vorbeigeführten Papierstreifen auf.
Bezeichnet man mit Z = S1
+ S2 den Zug, welchen
der Riemen auf die Achse B ausübt, mit u den Coefficienten des auf den Scheibenumfang
reducirten Reibungs- und Riemensteifigkeitswiderstandes für die Scheiben I und II, mit u1 den gleichen
Coefficienten für die Scheiben H1
und H2, so ergibt sich für
die auf Drehung des Hebelsystemes wirkende Kraft F,
welcher die Federspannung proportional ist:
F=S_1+{S_1}'-S_2-{S_2}'=2\,K\,\left(\frac{1}{1-{u_1}^2}\right)+2\,u\,Z.
Für den Leergang ist K = o,
also die Drehkraft
F_0=2\,u\,.\,Z.
Für die Umfangskraft K aber findet sich
F-F_0=F_1=2\,K\,\left(\frac{1}{1-{u_1}^2}\right).
also
K=\frac{F_1}{2}\,.\,(1-{u_1}^2).
Da u12 stets ein sehr kleiner Bruch ist, so kann man
also die Spannungen F1,
welchen wieder die Ordinaten der Diagramme entsprechen, einfach den Umfangskräften
proportional setzen; der Widerstand u hat auf dieselben
gar keinen, der Widerstand u1 nur einen verschwindenden Einfluſs.
Beispielsweise findet sich für das Dynamometer Nr. I (vgl. Tabelle am Schlusse):
u
1
K
==
0,01530,999766 \frac{F_1}{2},
für das Dynamometer Nr. V aber:
u
1
K
==
0,07220,9998572 . \frac{F_1}{2},
was offenbar vom praktischen Standpunkte aus als absolut genau
anzusehen ist.
Zu beachten ist, daſs nach jedesmaligem Spannen des Riemens ein Leergang-Diagramm
genommen werden und der Nullbleistift von Neuem eingestellt werden muſs.
Die Bánki'schen Kraftmesser werden in 6 Gröſsen gebaut,
über deren wesentlichste Verhältnisse nachstehende Tabelle Auskunft gibt
Nummerdes Dynamo-meters
Breite desTreibriemens
DurchmesserderScheiben
Uebertragbare Pferdekräfte bei den
Riemen-geschwindigkeiten von
5m
10m
15m
20m
25m
30m
I
40
200
1¼
2½
4
5
6½
8
II
70
300
3
6
9
12
15
18
III
120
400
7
14
21
28
35
42
IV
180
500
10½
21
32
42
53
63
V
250
600
17
34
51
68
85
102
VI
350
700
25
50
75
100
125
150
Tafeln