| Titel: | Die Raoult'sche Methode der Molekulargewichtsbestimmung; von Constantin Klinge. |
| Autor: | Constantin Klinge |
| Fundstelle: | Band 273, Jahrgang 1889, S. 179 |
| Download: | XML |
Die Raoult'sche Methode der
Molekulargewichtsbestimmung; von Constantin Klinge.
(Mit Abbildungen auf Tafel 11.)
Die Raoult'sche Methode der
Molekulargewichtsbestimmung.
Dank der Anregung, welche Paterno und NasiniBerichte, XIX, 2530., sowie
Victor MeyerBerichte, XXI, 539. gegeben,
hat die Raoult'sche Methode der
Molekulargewichtsbestimmung im Laufe der letzten zwei Jahre gewaltige Fortschritte
erfahren.
Trotzdem die diesbezügliche Literatur leider verschiedene Widersprüche, sowie bis
jetzt noch offen stehende Fragen aufzuweisen hat, so ist doch durch zahlreiche
Forscher, welche sich mit diesem Thema eingehend beschäftigt haben, theils durch
wissenschaftliche Grundlagen, theils durch praktische Verbesserungen bezieh.
Vereinfachungen des Verfahrens, die Methode gegenwärtig auf einen Standpunkt der
Entwickelung gelangt, welcher jedem Chemiker in einer groſsen Anzahl von Fällen
gestattet, sich dieser Methode der Molekulargewichtsbestimmung ohne gröſsere
Schwierigkeiten und mit geringen Hilfsmitteln zu bedienen.
Die Fülle von Arbeiten, welche über diesen Gegenstand in den verschiedensten
Zeitschriften veröffentlicht worden sind, haben den Verfasser bewogen, eine
einheitliche Darlegung der Methode, so weit das bis jetzt überhaupt durchführbar
ist, zu geben.
Bei Abfassung der nachstehenden Abhandlung ist das Hauptgewicht auf eine eingehende
Besprechung der praktischen Anwendung der Methode gelegt worden, um allen
denjenigen, welche in Zukunft derartige Molekulargewichtsbestimmungen auszuführen
gedenken, einen kurzen Leitfaden an die Hand zu geben, woher denn auch von der
Besprechung einiger theoretischer Fragen, welche in das Bereich der mathematischen
Physik gehören und zur Zeit zum Theil auch noch keine genügende Beantwortung
gefunden haben, Abstand genommen worden ist.
Der Abhandlung liegen die. Arbeiten von: F. M. Raoult,
Paterno, van t'Hoff, Victor Meyer, K. Auwers, Ostwald, Beckmann, Hollemann,
Hentschell, Fabinyi und Eykmann zu Grunde.
I. Theoretischer Theil.
Das Prinzip der Methode beruht auf der Beobachtung, daſs der Erstarrungspunkt irgend
eines lösenden Mediums bei Gegenwart einer in demselben gelösten fremden Substanz
herabgedrückt wird.
Umfassende Untersuchungen, welche früher von BladgenPhil. trans., LVIII, 277.,
RüdorffPogg. Ann., CXIV, 63. CXVI,
55. und CoppetAnn. chim. phys., [4] XXIII, 366. XXV, 502.
XXVI, 98. mit wässerigen Lösungen, in neuester Zeit von
RaoultAnn. chim. phys., [5] XX, 217. XXVIII, 133.
[6] II, 66, 93, 99, 115. IV, 401. VIII,
289, 317. Compt. rend., CII,
1307. auch mit einer Reihe von anderen lösenden Medien
angestellt worden waren, hatten zur Erkenntniſs bestimmter Gesetzmäſsigkeiten
bezüglich des Einflusses geführt, welchen die chemische Natur und die Menge eines
gelösten Körpers auf den Erstarrungspunkt des Lösungsmittels ausüben, und auf dieser
Grundlage arbeitete Raoult eine neue Methode der
Molekulargewichtsbestimmung aus.
Ueber die Gesetze, durch welche Raoult seine Methode
begründet, hat K. AuwersBerichte, XXI, 701. folgende
kurze Zusammenstellung gegeben:
Die Erniedrigung des Erstarrungspunktes (Depression), welche ein Lösungsmittel durch
Auflösen eines festen, flüssigen oder gasförmigen Körpers erfährt, ist innerhalb
gewisser Grenzen und unter gewissen Bedingungen der Menge des gelösten Körpers
direkt, der Menge des Lösungsmittels aber umgekehrt proportional.
Bezeichnet man mit C die Depression, welche durch Pg Substanz in Lg Lösungsmittel
hervorgebracht werden, mit A dieselbe Gröſse für 1g Substanz und 100g Lösungsmittel, so gilt die Gleichung:
A=\frac{C\,.\,L}{P\,.\,100}
Multiplicirt man die Gröſse A, welche Raoult den Depressionscoefficienten (coefficient
d'abaissement) der betreffenden Substanz für das betreffende Lösungsmittel nennt,
mit dem Molekulargewicht der gelösten Substanz M, so
erhält man nach der Gleichung
M . A =
T
die sogen. molekulare Depression des fraglichen Körpers. Für
jeden Körper ändert sich der Werth von A und folglich
auch von T mit der Natur des Lösungsmittels; dagegen
ergab sich aus den genannten Untersuchungen, besonders denen von Raoult, daſs bei Anwendung desselben Lösungsmittels der
Werth von T für gröſse Klassen chemisch analog
zusammengesetzter Stoffe einen constanten oder doch annähernd constanten Werth
annimmt, mit anderen Worten, daſs Verbindungen von analoger chemischer Constitution
gleiche Molekulardepressionen besitzen.
Raoult fand jedoch noch allgemeinere, umfassendere
Gesetzmäſsigkeiten auf. Berechnet man nämlich nicht die Depression, welche 1g Substanz in 100g Lösungsmittel hervorruft, also die Gröſse A, sondern diejenige Depression, welche durch Auflösung von einem Molekül
der betreffenden Substanz in 100 Molekülen des Lösungsmittels bewirkt wird, so erhält man, wenn M, wie früher, das Molekulargewicht des gelösten, M1 dasjenige des
lösenden Körpers ausdrückt, die Gleichung:
\frac{M}{M_1}\,.\,A=\frac{T}{M_1}=T_1.
Aus derselben ergibt sich zunächst unmittelbar, daſs die neue Gröſse T1 einen constanten
Werth besitzt, so lange T constant bleibt. Führt man
aber diese Rechnungen für eine Anzahl verschiedener Lösungsmittel durch, so gelangt
man zu dem höchst bemerkenswerthen Ergebnisse, daſs, obwohl die Gröſse T, wie erwähnt, von einem Medium zum anderen ihren
Werth ändert, und zwar in erheblichster Weise, die Gröſse T1 dennoch mit groſser Annäherung constant
bleibt. Bezeichnet man mit t1, t2, t3.... die Werthe von
T für eine Anzahl beliebiger Lösungsmittel, mit m1, m2, m3.... die
Molekulargewichte der letzteren, so gilt mithin:
\frac{t_1}{m_1}=\frac{t_2}{m_2}=\frac{t_3}{m_3}=T_1=\
\mbox{Const}.
Der Werth der Constanten schwankt nach den Versuchen von Raoult zwischen 0,59° und 0,65° und ist im Mittel
gleich 0,63° zu setzen. In Worten lautet das GesetzAnn. chim. phys., [6] II, 92.: Löst
man 1 Molekül einer beliebigen Substanz in 100 Molekülen eines beliebigen
Lösungsmittels, so wird der Erstarrungspunkt des letzteren um 0,63°
herabgedrückt.
Dieses Gesetz bezeichnet Raoult mit dem Namen des
„allgemeinen Gesetzes der Erstarrung“ (loi générale de la congélation).
Dieses Gesetz gilt zunächst für das Temperaturintervall 0 bis 80° C., da der
Schmelzpunkt aller der von Raoult benutzten
Lösungsmittel innerhalb dieser Grenzen lag, während noch zu untersuchen bleibt, ob
das Gesetz seine Gültigkeit behält auch für Medien, welche einen höheren oder
niedrigeren Schmelzpunkt besitzen.
Aber auch innerhalb des bezeichneten Intervalls gilt das Gesetz nicht ausnahmslos.
Bei seiner soeben gegebenen Formulirung ist stillschweigend die Voraussetzung
gemacht, daſs der Werth von T bei gleichbleibendem
Lösungsmittel nicht allein innerhalb groſser Körperklassen constant bleibe, wie dies
oben als der Wirklichkeit entsprechend ausgeführt ist, sondern daſs diese Constanz
überhaupt für alle Körper gelte. Zieht man nur die organischen Verbindungen in den
Kreis der Betrachtung, so scheint es in der That eine Reihe von Lösungsmitteln zu
geben, welche letzterer Forderung genügen, d.h. sämmtliche organische Substanzen
zeigen in ihnen die nämliche molekulare Depression. Bei einer Reihe anderer Medien
ist die Bedingung wenigstens für die weitaus überwiegende Mehrzahl der Substanzen
erfüllt, während eine kleine Menge von Körpern – regelmäſsig Alkohole, Phenole und
Säuren – in denselben Depressionen hervorrufen, welche nur halb so groſs sind wie
die „normalen“ der übrigen Substanzen.
Ein gänzlich abweichendes Verhalten von allen übrigen untersuchten Lösungsmitteln,
die sämmtlich in der erwähnten mehr oder weniger vollkommenen Weise dem allgemeinen
Gesetz der Erstarrung gehorchen, zeigt jedoch das Wasser, das ja auch in vielen
anderen Beziehungen eine besondere Stellung einnimmt. Allerdings besitzen, nach den
bis jetzt vorliegenden Erfahrungen, alle organischen Substanzen im Wasser eine
annähernd gleiche molekulare Depression T, allein aus
derselben berechnet sich nicht der normale Werth T1 = 0,63, sondern ein Werth, der etwa zwischen 0,92°
und 1,27° schwankt.
Noch weniger trifft das allgemeine Gesetz auf wässerige Lösungen anorganischer
Substanzen zu, indem bei diesen T für jede Klasse von
Salzen einen besonderen Werth annimmt. Da es sich jedoch in erster Linie darum
handelt, die Methode zur Molekulargewichtsbestimmung organischer Substanzen, welche
ja, wie gesagt, dem Raoult'schen Gesetze unterworfen
sind, nutzbar zu machen, so soll auf die soeben erwähnten abnormen Verhältnisse
nicht weiter eingegangen werden, zumal dieselben zur Zeit noch keine genügende
Beurtheilung zulassen.
Wie schon oben bemerkt, rufen verschiedene organische Substanzen in einigen
Lösungsmitteln Depressionen hervor, welche nur halb so groſs sind wie die normalen
der übrigen Substanzen. – Demgemäſs gibt auch Raoult
für jedes Lösungsmittel stets zwei Werthe der molekularen Depression T an.
T
normal
anormal
Wasser
19
9,5
Benzol
49
25,0
Eisessig
39
18,5
Naphtalin
82
41,0
Die Substanzen, welche anormale Depressionen zeigen, existiren nur in kleiner Zahl,
und meist ist dieselbe nicht gleich für die verschiedenen Lösungsmittel; die
Essigsäure bietet eine sehr kleine Zahl von Ausnahmen dar, während das Benzol die
Hälfte der normalen Depression für die Alkohole, die Säuren und die Phenole nach den
Untersuchungen von Raoult und auch für die Oxime nach
denjenigen von BeckmannBerichte, XXI, 766. ergibt,
und ist es erwähnenswerth, daſs diese Körper, welche in jedem Lösungsmittel normale
und anormale Depression hervorrufen, wohlbestimmten Gruppen angehören.Raoult, Ann. chim. phys., [6] II, 88. Paterno, Berichte, XXII, 465.
Das Raoult'sche Gesetz, welches sich lediglich auf eine
experimentelle Grundlage stützt, ist rein empirisch, und seine Gültigkeit, wie es
sich schon am Wasser gezeigt hatte und neuerdings aus den Arbeiten von HentschellZeitschr. für phys. Chem., II,
306. hervorgeht, keineswegs allgemein.
Nach OstwaldZeitschr. für phys. Chem., II,
311. würde der Satz von Raoult
dann allgemeine Gültigkeit haben, wenn die molekulare latente Schmelzwärme dem
Quadrat der absoluten Schmelztemperatur proportional wäre; dies scheint thatsächlich
in einigen Fällen stattzufinden, aber nicht in allen.
Dagegen hat van t'HoffZeitschr. für phys. Chem., I,
497. der Methode eine sichere wissenschaftliche Grundlage
gegeben.
Derselbe beweist durch die homologen Beziehungen, welche das Lösen und Verdampfen der
Körper in Bezug auf ihre molekularen Verhältnisse zeigen, daſs die molekulare
Depression eines Lösungsmittels in einfacher Beziehung zur latenten Schmelzwärme
dieses Lösungsmittels steht.
Bezeichnet man mit T die absolute Erstarrungstemperatur
(also Erstarrungstemperatur + 273) des Lösungsmittels und mit W die latente Schmelzwärme desselben, so läſst sich
nach der Formel
0,02\,.\,\frac{T^2}{W}=t
die molekulare Depression berechnen.
Diese Formel ist thermodynamisch begründet und daher allgemein gültigZeitschr. für phys. Chem., II,
311..
Die nach dieser Formel von van t'Hoff berechneten Werthe
stimmen thatsächlich mit denjenigen, welche RaoultAnn. chim. phys., [5] XXVIII. [6]
XI. durch zahlreiche Versuche festgestellt hatte, vollkommen
überein.
Lösungsmittel
Gefrierpunkt T
Lat. Schmelz-wärme W
t=\frac{0,02\,.\,T^2}{W}
Mol.Depression
Wasser
273
79
18,9
18,5
Essigsäure
273 + 16,7
43,2 * †
38,8
38,6
Ameisensäure
273 + 8,5
55,6 * †
28,4
27,7
Benzol
273 + 4,9
29,1 †
53,0
50,0
Nitrobenzol
273 + 5,3
22,3 †
69,5
70,7
* Berthelot, Essai de mecanique
chimique.
† Petterson, Journal für praktische
Chemie (2) XXIV, 129.
Für ein bei 38° schmelzendes Phenol berechnete EykmannZeitschrift für phys. Chem., III,
113. nach der van t'Hoff'schen
Formel die Constante T = 76, während die molekulare
Depression des Phenols, aus der Raoult'schen Formel
(0,62 × Molekulargewicht des Phenols) berechnet, bloſs 58,3 beträgt. Zahlreiche
Versuche, welche Eykmann mit Phenol gemacht hat, um
experimentell die molekulare Depression dieses Körpers festzustellen, haben zu einem
Werthe geführt, der mit dem van t'Hoff'schen
übereinstimmt.
Für Naphtalin gibt RaoultCompt. rend., CII. 1307. die
molekulare Depression T = 82 an, während nach der van t'Hoff'schen Formel sich dieser Werth auf 69,4 berechnen läſst. R. FabinyiZeitschr. für phys. Chem., III,
38. erhält nun für Naphtalin einen Werth T = 70, welcher sich dem Raoult'schen nähert, jedoch erweist sich umgekehrt aus den Untersuchungen
Eykmann'sZeitschr. für phys. Chem., III, 113.,
daſs die molekulare Depression des Naphtalins mit dem aus der van t'Hoff'schen Formel berechneten Werthe
übereinstimmend ist.
Diese Widersprüche können zum Theil darin eine Erklärung finden, daſs Raoult mit einer willkürlich gewählten Concentration
des Lösungsmittels arbeitete und seine Werthe für die molekularen Depressionen daher
immer die gleichen bleiben, unabhängig von der Concentration des lösenden
Mediums.
Durch die van t'Hoff'sche Relation ändert sich die
molekulare Depression eines Lösungsmittels stetig mit der Concentration desselben,
da der Erstarrungspunkt, welcher ja mit der Concentration immer wechselt, ein
Hauptfactor der Formel ist.
Ueberhaupt spielt die Concentration des Lösungsmittels bei der praktischen
Durchführung der Methode eine äuſserst wichtige Rolle. Die Raoult sehen Gleichungen gelten nur für sehr verdünnte Lösungen.
Bei zunehmender Concentration des Lösungsmittels ergibt sich meist ein gleichmäſsiges
Ansteigen der Molekulargewichte. Diese Verhältnisse hat BeckmannZeitschr. für phys. Chem., II,
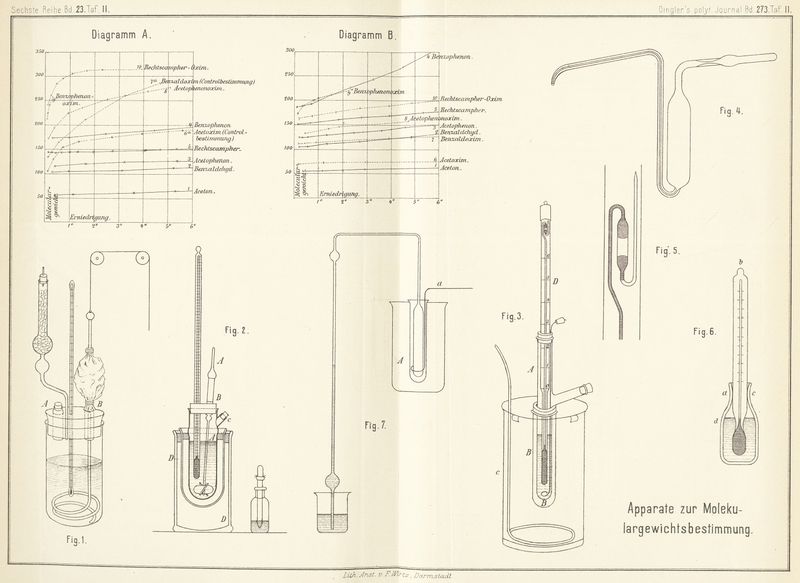
719. durch Curventafeln veranschaulicht, in welchen die
beobachteten Depressionen als Abscissen, die Molekulargewichte als Ordinaten
eingetragen sind (Fig. A und B Taf. 11).
Dieses Ansteigen der Werthe erklärt BeckmannZeitschr. für phys. Chem., II
740. aus der Veränderlichkeit der molekularen Depressionen
mit der Erstarrungstemperatur, auf welchen Umstand vorhin schon aufmerksam gemacht
wurde.
Andererseits aber darf die Verdünnung auch nicht unter ein gewisses Maaſs
herabsinkenAuwers, Berichte, XXI, 705., wenn man
zu normalen Werthen gelangen will.
So gibt beispielsweise RaoultAnn. chim. phys., [6] VIII,
259. als Grenzen für die regelmäſsigen Werthe, bei Anwendung von
Benzol als Lösungsmittel, Depressionen an, welche zwischen 0,5° und 2,5° liegen,
doch hat neuerdings BeckmannZeitschr. für phys. Chem., II,
718. bei Depressionen von 0,2° und weniger schon brauchbare
Werthe erhalten.
Eine Hauptbedingung für die Anwendbarkeit der Raoult'schen Methode ist, daſs zwischen der gelösten Substanz und dem lösenden
Medium keine chemische Wirkung stattfindet.Auwers, Berichte, XXI, 705.
Ausgenommen sind hierbei die Fälle, in denen die gedachte Wirkung sich auf ein
einfaches Zusammentreten der beiden Körper nach bekannten Gewichtsverhältnissen beschränkt, wie z.B. bei
der Auflösung eines der Hydratbildung fähigen Körpers in Wasser oder einer
organischen Base in Eisessig u.s.w. Man hat in diesen Fällen nur die Menge l des Lösungsmittels, welche von den Pg gelöster Substanz
fixirt werden, entsprechend in Rechnung zu tragen, wodurch die Gleichung
A=\frac{C\,.\,L}{P\,.\,100}
in die Form
A=\frac{C\,.\,(L-l)}{(P+l)\,.\,100}
übergeht.
Hiermit mögen die Gesetzmäſsigkeiten, auf welche sich die Methode stützt, sowie die
Bedingungen, unter welchen dieselben zutreffen, genügend skizzirt sein.
Bemerkt sei noch, daſs RaoultAuwers, Berichte, XXI, 704.
bei der Untersuchung von etwa 150 organischen Verbindungen nur zweimal zu
Ergebnissen gelangte, die mit der gebräuchlichen Formulirung der Körper in
Widerspruch standen; für Jodoform und Morphin fand er nämlich die Molekulargewichte
doppelt so groſs, als dieselben allgemein angenommen werden.
Aus den neueren Untersuchungen von PaternoBerichte, XXII, 465. ergibt
sich jedoch, daſs die durch das Jodoform bewirkte Depression des Benzols als normal
angesehen werden muſs und daſs, wenn sie sich wirklich von der Norm entfernt, dies
im entgegengesetzten Sinne erfolgt, um eine höhere molekulare Complexität
anzunehmen, und sie würde höchstens beweisen, daſs das Jodoform eine theilweise
Zersetzung erleidet, was auch thatsächlich der Fall zu sein scheint. Ueberhaupt sind
alle Abnormitäten höchst wahrscheinlich auf Dissociationserscheinungen
zurückzuführen.
II. Praktischer Theil.
Will man das Molekulargewicht eines beliebigen Körpers mittels der Raoult'schen Methode bestimmen, so wird es sich
empfehlen, die molekulare Depression T des gewählten
Lösungsmittels zuerst theoretisch, mit Hilfe der van
t'Hoff'schen Formel, zu berechnen, und dann dieselbe Gröſse durch Versuche
mit Substanzen von bekanntem Molekulargewichte experimentell festzustellen.
Ist dies geschehen, so findet man das Molekulargewicht jeder Substanz, indem man
durch eine Reihe von Versuchen den Depressionscoefficienten A bestimmt und mit dem gefundenen Werthe in T
dividirtAuwers, Berichte, XXI, 704.:
M=\frac{T}{A}
Mit der Raoult'schen Methode erhält man im Allgemeinen
keine absolut genauen
Werthe für die Molekulargewichte, sondern nur Näherungswerthe.
Was die Schärfe der Resultate anlangt, die man mit der Methode zu erreichen vermag,
so bemerkt K. AuwersBerichte, XXI, 708., daſs
dieselbe wesentlich durch zwei Punkte bestimmt wird: erstens durch die Strenge, in
der das Raoult'sche Gesetz überhaupt gültig ist, und
zweitens durch den Grad der Genauigkeit, mit dem man den Erstarrungspunkt der
Lösungen zu bestimmen vermag.
Der erste Punkt braucht nach dem, was im theoretischen Theile gesagt worden ist,
nicht näher erörtert zu werden; was jedoch den zweiten Punkt anbelangt, so ist die
Genauigkeit der Resultate einerseits von der Wahl des Apparates, andererseits aber
von der Wahl und Concentration des Lösungsmittels abhängig.
Die Apparate.
Das von Raoult ursprünglich angewandte Verfahren hat auf
Grund neuerer Untersuchungen über diesen Gegenstand mannigfache Abänderungen
erlitten, und sind namentlich in der letzten Zeit verschiedene Apparate zur
Bestimmung des Molekulargewichtes aus der Gefrierpunktserniedrigung in Vorschlag
gebracht worden, deren Einrichtung und Handhabung jetzt näher besprochen werden
soll.
Apparat von AuwersBerichte, XXI, 711. (Fig. 1 Taf.
11). Der untere Theil eines Glasmantels, wie er zur Umhüllung von
Dampfdichteapparaten dient, wird abgesprengt, und dieses Gefäſs, etwa 4,5 bis 5cm weit und 13 bis 16cm hoch, durch einen vierfach durchbohrten Korkstopfen verschlossen. In
die mittlere Bohrung wird das Thermometer eingesetzt, und zwar so tief, daſs seine
Kugel sich in der Mitte der Flüssigkeit befindet. Hinter dem Thermometer befindet
sich eine Röhre mit Chlorcalcium, um die bei der Abkühlung des Apparates
einströmende Luft zu trocknen. In der Bohrung A steckt
eine kurze, weite Glasröhre, die ihrerseits durch einen kleinen Kork verschlossen
ist; diese Röhre wird nur geöffnet, wenn durch sie ein Krystall von Eisessig in die
Flüssigkeit geworfen wird, um die Erstarrung einzuleiten. In die Bohrung B ist gleichfalls eine kurze Glasröhre eingesetzt, in
der sich der Stab der Rührvorrichtung aus Glas auf und ab bewegt. Um den kleinen
Zwischenraum zwischen Röhre und Stab – in der Skizze der Deutlichkeit halber weiter
gezeichnet als in Wirklichkeit – von der Luft abzuschlieſsen, was durchaus
nothwendig ist, wenn man eine Reihe von Versuchen mit derselben Lösung anstellen
will, wird ein kleiner Ballon aus sehr dünnem Gummi mit Ansatzstück, wie sie
gelegentlich zu Vorlesungszwecken benutzt werden, in den man oben ein Loch
geschnitten hat – oder ein sehr dünnwandiger, weiter Gummischlauch – über Röhre und
Glasstab gezogen und an denselben so befestigt, daſs er den Bewegungen des Rührers
folgen kann, ohne dieselben zu hindern oder selbst gespannt zu werden. Zur sicheren
Befestigung werden über Röhre und Glasstab kurze, dicke, eng anliegende Stückchen
Gummischlauch gezogen und an ihnen der Ballon mit Seide festgebunden. Der ganze
Apparat wird in eine Klammer an einem Stativ eingespannt. In eine zweite, höher
befindliche Klammer ist ein Stückchen Holz eingespannt, an welchem um ein Paar Nägel
zwei Rollen drehbar sind, die man sich aus eingekerbten Korkstückchen herstellen
kann. Ueber die Rollen läuft ein seidener Faden, der mittels eines Platinöhres an
dem Stab des Rührwerkes befestigt ist; durch eine passende Uebertragung kann man das
Rührwerk mit einer kleinen Turbine in Verbindung setzen, oder man bewegt dasselbe
während des Versuches mit der Hand, was die Beobachtung in keiner Weise stört.
Zur Messung der Temperatur wird ein gewöhnliches Thermometer benutzt, welches von 0
bis 50° in 1/10
Grade getheilt ist. Die Ablesung geschieht mit einer Lupe, die in passender
Entfernung vor der Scala an einem kleinen Stativ eingespannt wird.
Mittels einiger Uebung gelingt es, Auge, Lupe und Theilung stets in die gleiche Lage
zu einander zu bringen; nötigenfalls kann die Ablesung auch mit einem Fernrohre
geschehend was anfangs zur Controle der direkten Ablesungen empfehlenswerth ist. –
Die Körperwärme des in groſser Nähe befindlichen Beobachters kann keinen merklichen
Einfluſs auf die Angaben des Thermometers ausüben, da nach den Beobachtungen von Raoult, selbst wenn die Temperatur der Gesammtumgebung
des Apparates während des Erstarrungsprozesses um 20° geändert wird, die Differenzen
in den Angaben nie mehr als 0,01° betragen. Der mögliche Fehler der Ablesung beträgt
etwa 0,005 bis 0,01°; hierzu kann noch ein möglicher Fehler der Theilung treten,
dessen Betrag etwa eben so hoch geschätzt werden darf. Die Bestimmung des
Erstarrungspunktes kann also, was die beiden erwähnten Fehlerquellen anlangt, im
ungünstigsten Falle bis zu ± 0,02° fehlerhaft ausfallen. Jedoch darf angenommen
werden, daſs diese extremen Fälle nur äuſserst selten vorkommen; der
durchschnittliche Fehler würde vielmehr ± 0,01° nicht übersteigen. Auch müssen
jedesmal eine Reihe von Controlbestimmungen angestellt werden, um etwaige Fehler der
Einzelbestimmungen möglichst auszugleichen.
Jedenfalls ist aber, falls man nicht in der Lage ist, geprüfte Thermometer mit
feinerer und weiterer Theilung zu benutzen, auf eine möglichst genaue Ablesung des
Thermometers das gröſste Gewicht zu legen, da schon eine verhältniſsmäſsig kleine
Ungenauigkeit hierbei den Werth einer Bestimmung gänzlich illusorisch machen kann.
Die Versuche wurden von Auwers in folgender Weise
angestellt: In das Gefäſs wurden etwa 100g EisessigAuwers hat mit Eisessig die besten Resultate
erzielt und daher denselben ausschlieſslich als Lösungsmittel
angewandt. abgewogen – es genügt, bis auf zehntel Gramme zu wägen –
und darauf der Apparat in ein groſses Becherglas mit Wasser gesenkt, dessen
Temperatur sich etwa 1 bis 2° unter der jedesmaligen Erstarrungstemperatur befand,
also im Mittel etwa 14° betrug. Unter beständigem Rühren wurde der Eisessig langsam
bis etwa ¼ bis ½° unter seinen Erstarrungspunkt abgekühlt und darauf durch einen
eingeworfenen Krystall die Erstarrung eingeleitet. Zunächst sank der
Quecksilberfaden noch um 2 bis 3 zehntel Grade, darauf stieg er erst rasch, dann
langsamer, um nach kurzer Zeit seinen höchsten Stand zu erreichen, auf dem er lange
Zeit unbeweglich verharrte; danach begann er äuſserst langsam zu sinken. Während der
ganzen Operation wurde das Rührwerk bewegt. Man braucht das Sinken des Quecksilbers
nicht abzuwarten, sondern kann den Versuch unterbrechen, sobald man sicher ist, daſs
sich die Kuppe des Quecksilbers fest eingestellt hat. Dieser höchste Stand des
Thermometers wurde nach Raoult als der wahre
Erstarrungspunkt angenommen. – Nach Beendigung des Versuches wurde der Apparat auf
ein Wasserbad gesetzt, doch so, daſs er nicht von den Dämpfen umspült werden konnte;
der Eisessig, von dem nur ein kleiner Theil erstarrt war, wieder völlig aufgethaut
und nun sofort die zweite Bestimmung des Erstarrungspunktes des Eisessigs in der
nämlichen Weise wie die erste vorgenommen u.s.f. Hierbei zeigte es sich, daſs der
fragliche Punkt in der Regel bei der zweiten Bestimmung gegenüber der ersten um
0,01°, 0,02°, auch 0,03° herabgedrückt war; in einigen Fällen zeigte sich auch bei
der dritten Bestimmung eine nochmalige kleine Depression gegenüber der zweiten, die
jedoch nie mehr als 0,005° betrug. In anderen Fällen ergaben die beiden ersten
Bestimmungen denselben oder fast denselben Werth für den Erstarrungspunkt, alsdann
trat die stärkere Depression bei der dritten Bestimmung auf.
In allen Fällen ergab jedoch meist die dritte, spätestens die vierte Bestimmung einen
Werth, der nun bei allen weiteren zur Controle unternommenen Bestimmungen sich als
völlig constant erwies.
Es mag dahin gestellt bleiben, wie diese anfänglichen Unregelmäſsigkeiten zu erklären
sind, bei denen jedenfalls die Feuchtigkeit, die zu Anfang jeder Versuchsreihe an
den Wänden des Apparates und im Inneren des Ballons haftet, eine wesentliche Rolle
spielt: aus der Thatsache ergab, sich die praktische Regel, nie früher Substanz in
den Apparat zu bringen, bevor nicht der Eisessig einen constanten Erstarrungspunkt
zeigte. Sobald dies der Fall war, wurde eine abgewogene Menge Substanz – es genügt,
bis auf Milligramme zu wägen – in den Apparat gebracht, durch Rühren aufgelöst,
nöthigenfalls unter gleichzeitigem, gelindem Erwärmen, und darauf wie beim reinen
Eisessig in der Regel dreimal hinter einander der Erstarrungspunkt des Gemisches bestimmt. – Die
erhaltenen Werthe zeigten zwischen der ersten und dritten Bestimmung eine Differenz
von höchstens 0,01°. Hierauf wurde eine neue Menge. Substanz zugegeben und abermals
in der Regel drei Versuche angestellt, die mit derselben Annäherung unter einander
übereinstimmten. Bei dieser zweiten Reihe von Versuchen wurden sämmtliche
Depressionen auf den Erstarrungspunkt bezogen, der sich bei der letzten Bestimmung
der ersten Reihe ergeben hatte. Was die Zeit anlangt, die diese Versuche in Anspruch
nahmen, so erforderte eine einzelne Bestimmung etwa 10 Minuten; eine ganze Reihe von
gewöhnlich 11 zusammengehörigen Bestimmungen lieſs sich mit den dazu nöthigen
Vorbereitungen und Wägungen bequem in 3 bis 4 Stunden ausführen.
Die Schärfe der Resultate, welche Auwers mit seinem
Verfahren erzielt hat, sind aus folgendem VersuchsbeispieleBerichte, XXI, 715. ersichtlich. In
der Tabelle bedeutet:
E den Erstarrungspunkt der Lösungen,
C die beobachtete Depression,
A die für 1g Substanz
und 100g Eisessig berechnete Depression,
M das daraus berechnete Molekulargewicht.
Die Zahlen sind mit Hilfe des von Raoult für die
molekulare Depression des Eisessigs aufgestellten Werthes T = 39 berechnet.
Naphtalin, C10H8, M = 128.
Erstarrungspunkt des Eisessigs: 16,100°.
Angewandt: 1g,7865 Naphtalin in 101g,0 Eisessig. Gefunden:
E
C
A
M
15,595°
0,505°
0,286°
136
15,595°
0,505°
0,286°
136
15,595°
0,505°
0,286°
136
–––––
––––
0,286°
136.
Zugesetzt: 0g,7937 Naphtalin. Gefunden:
E
C
A
M
15,380°
0,215°
0,247°
142
15,380°
0,215°
0,247°
142
15,380°
0,215°
0,247°
142
–––––
––––
0,247°
142.
Theorie
Mittel der Versuche
M = 128
M = 139.
(Schluſs folgt.)
Tafeln