| Titel: | Edoux' Fahrstuhl auf dem Eiffelthurm. |
| Autor: | Pr. |
| Fundstelle: | Band 273, Jahrgang 1889, S. 251 |
| Download: | XML |
Edoux' Fahrstuhl auf dem Eiffelthurm.
Mit Abbildungen auf Tafel
12.
Edoux' Fahrstuhl auf dem Eiffelthurm.
Von der zweiten Plattform bis zur Spitze des Eiffelthurmes, für eine Förderhöhe von
160m,4 ist nach Edoux' System ein Fahrstuhl mit zwei Kammern angenommen, welche sich in
halber Förderhöhe (80m,2) gleichstellen.Vgl. Zeitschrift des Vereins deutscher
Ingenieure, 1888 Bd. 32 * S. 1016 und 1042. Beide sind
mit über Rollen laufende Kabel derart verbunden, daſs dem Aufstieg der einen Kammer
in der oberen Weghälfte die Niederfahrt der anderen in der unteren Hälfte
entspricht. Weil aber die eine mittels Druckkolben gehobene Kammer A nur die obere Weghälfte von 80m,2, dagegen die an Kabeln hängende Kammer B nur die untere Förderhöhe befährt, so ist an der
Zwischenplattform ein Umsteigen der Fahrgäste aus einer Kammer in die andere
erforderlich. Diese Anordnung bietet den groſsen Vorzug einer vortheilhaften
Gewichtsausgleichung, Einfachheit und Sicherheit des Betriebes.
Die hierbei zu erfüllenden Bedingungen hat A. Käs in der
Oesterreichischen Zeitschrift für Berg- und
Hüttenwesen, 1889 Bd. 37 Nr. 3 * S. 25, dargelegt, deren gedrängte
Wiedergabe hier gestattet sei.
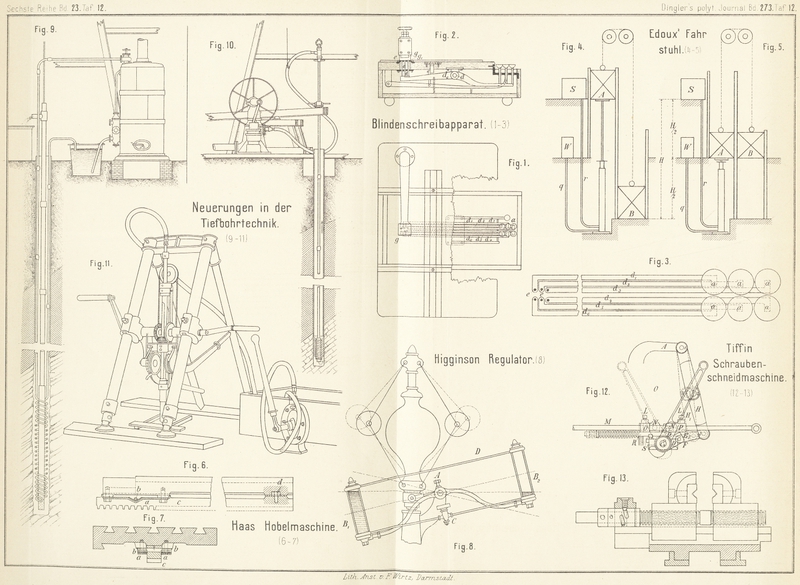
An der Thurmspitze, in H = 160m,4 Höhe, ist der Sammelkasten S (Fig. 4 und 5) für das Druckwasser, an
der Wechselstelle in der Höhe ½ H ist der Behälter für
das Rücklaufwasser angeordnet. Aus diesem entnehmen die tieferliegenden Preſspumpen das
Betriebswasser und heben es nach S. Die Rohrleitungen
r und q stellen die
Verbindung der beiden Treibröhren mit den Behältern S
und W her. Da sich die Gewichte der beiden Fahrkammern
ausgleichen, so bleibt die Nutzlast Q, das Eigengewicht
der Treibkolben G, das Gewicht des überhängenden Kabels
(p in 1k für 1m Länge) und die Wassersäule (γ = 1000k für 1cbm) in Rechnung zu ziehen, wobei η der Wirkungsgrad beim Kolbenfall und φ beim Kolbenaufstieg und f die Summe der Kolbenquerschnitte ist.
Bestimmung des Kabelgewichtes.
a) Bedingung für die Auffahrt zur Wechselstelle. B ist
belastet, A ist leer, Rohrleitung q offen. Beim Anhub (Fig. 4)
ηG = H . p +
Q. . . . . . . . 1)
beim Hubende an der Wechselstelle (Fig. 5)
ηG = 0,5 .γ
. H . f + Q . . . . . . . 2)
durch Gleichstellung folgt
p = 0,5 . γ
. f . . . . . . . . 3)
b) Bedingung für die Auffahrt von der Wechselstelle zur Thurmspitze. Kammer A ist belastet, B ist
leer, die Rohrleitung q geschlossen, r aber offen.
Beim Anhub (Fig.
5)
φ . γ . f . H = G + Q . . . . . . . 4)
beim Hubende an der Spitze (Fig. 4)
φ (0,5 γ . f . H + p .
H) = G + Q . . . . . 5)
Aus der Gleichsetzung folgt Gl. 3)
p = 0,5 γ . f.
Soll daher für diesen Fall die treibende Kraft gleichbleibenden Werth behalten, so
muſs das Kabelgewicht der Längeneinheit (1m)
gleich dem Gewichte einer Wassersäule sein, welche bei derselben Einheit die halbe
Fläche der Treibkolben zum Querschnitte hat,
p = γ(0,5 f)
Bestimmung des Treibkolbengesammtgewichtes G.
Bedingung für die Anfangsstellungen im Aufhube
ηG – p . H = Q . . . . . . . . 1)
und
φ . γ . f . H – G = Q . . . . . . . 4)
oder wenn für
γf = 2p
. . . . . . . . . 3)
gesetzt wird
φ . 2p . H –
G = Q . . . . . . . 4a)
Bei Gleichsetzung von 4a) und 1) folgt
G=\frac{1+2\,\varphi}{1+\eta}\,.\,p\,.\,H . .
. . . . 6)
während sich die Gesammtfläche der beiden Treibkolben aus Gl.
2) ergibt, wie folgt:
f=\frac{2\,(\eta\,G-Q)}{\gamma\,.\,H} . . . .
. . 7)
oder aus 3):
f=2\,\frac{p}{\gamma}
Wird dieser Werth für die Kolbenfläche in Gl. 7) gesetzt und das so gefundene p in die Gl. 6) eingeführt, so erhält man eine
unmittelbare Beziehung zwischen Kolbengewicht G und
Nutzlast Q.
G=\frac{Q}{\eta-\frac{1+\eta}{1+2\,\varphi}} .
. . . . . . . 8)
Werden sämmtliche Widerstände vernachlässigt, also η =
φ = 1 gemacht, so folgen als Näherungswerthe
G = 3Q
. . . . . . . . . 8)
f=\frac{4\,Q}{\gamma\,.\,H} . . . . . . .
7)
und
p=\frac{2\,.\,Q}{H} . . . . . . . . . 4a)
Die Verhältnisse des Edoux'schen Aufzuges am
Eiffelthurme in Rechnung gebracht, erhält man bei einer Förderhöhe H = 160m,4, Hub der
Treibkolben 0,5 H = 80m,2, Nutzlast oder Besetzung einer Kammer mit 60 Fahrgästen Q = 4000k, und da die
zwei gleichen Treibkolben, von denen jeder d = 32cm Durchmesser hat, ein Gesammtgewicht G = 19200k besitzen,
und da ferner das Gewicht eines Meters Kabelseil zu
\frac{p}{4}=20^k angegeben ist, demnach Gesammtgewicht der
vier Seile p = 80k
für 1m Länge, der Wirkungsgrad beim Kolbenfall η = 0,876 und für den Auf hub φ = 0,904, wegen verminderter Rollenzapfenreibung angenommen wird, so
folgt durch Rechnung für G = 19205k, für f = 0,16cm, entsprechend für einen Treibkolben 0,5 f = 0,08qm oder d = 32cm und für p = 0,5 . 1000 . 0,16 = 80k.
Pr.
Tafeln