| Titel: | Beschreibung des in Frankreich üblichen Verfahrens, den Bleigehalt der zinnernen Geräthschaften mittelst der hydrostatischen Wage auszumitteln. |
| Fundstelle: | Band 42, Jahrgang 1831, Nr. LXXV., S. 286 |
| Download: | XML |
LXXV.
Beschreibung des in Frankreich uͤblichen
Verfahrens, den Bleigehalt der zinnernen Geraͤthschaften mittelst der
hydrostatischen Wage auszumitteln.
Aus dem Dictionnaire technologique Bd. XVII. S.
338
Mit einer Abbildung auf Tab. V.
Ueber das Ausmitteln des Bleigehaltes der zinnernen
Geraͤthschaften
Die franzoͤsische Regierung ließ bekanntlich bei Einfuͤhrung der neuen
metrischen Maße fuͤr die Fluͤssigkeiten durch die HHrn. Fourcroy, Vauquelin, Darcet u.s.w. die Quantitaͤt
Blei aus Mitteln, womit man das Zinn legiren kann, ohne daß die daraus verfertigten
Maße und andere Geraͤthschaften, worin Nahrungsmittel aufbewahrt werden, der
Gesundheit nachtheilig sind. Diese Chemiker fanden, daß man ohne Gefahr achtzehn
Theile Blei mit zwei und achtzig Theilen Zinn legiren kann. Hiernach wurde der
Gehalt des legirten Zinnes durch Regierungsbeschluß auf 83 1/2 Procent festgesezt,
wobei man 1 1/2 Procent nachließ. Es war nun ein Verfahren noͤthig, wodurch
man leicht ausmitteln konnte, ob die verfertigten Gegenstaͤnde den
gesezmaͤßigen Gehalt haben; dieses gab die Physik an die Hand; es besteht
darin, das specifische Gewicht des Gefaͤßes, d.h. das Gewicht desselben in
Vergleich mit einem gleichen Volumen Wasser auszumitteln. Zu diesem Ende wiegt man
das Gefaͤß genau in der Luft und sodann im Wasser, indem man es ganz in
dasselbe taucht; und da es sodann so viel von seinem Gewichte verliert als sein
gleiches Volumen Wasser wiegt, so kann man leicht durch die Vergleichung der beiden
Gewichte finden, wie oft das Gewicht des Koͤrpers in der Luft das Gewicht
eines gleichen Volumens Wasser in sich enthaͤlt.
Man fand durch Versuche, daß eine Legirung von Zinn und Blei, welche 82 Procent Zinn
enthaͤlt, im Wasser 1288 Zehntausendtheile von ihrem Gewichte verliert, d.h.
wenn die Masse in der Luft 10,000 Theile wiegt, so wird sie im Wasser nur 8712
wiegen, daher das specifische Gewicht dieser Masse 7,764 ist. Jede Legirung in
demselben Verhaͤltniß von Zinn und Blei, wird im Wasser eben so viel von ihrem
Gewicht verlieren; sie wuͤrde mehr davon verlieren, wenn sie mehr Zinn
enthielte, und weniger, wenn sie weniger Zinn enthielte.
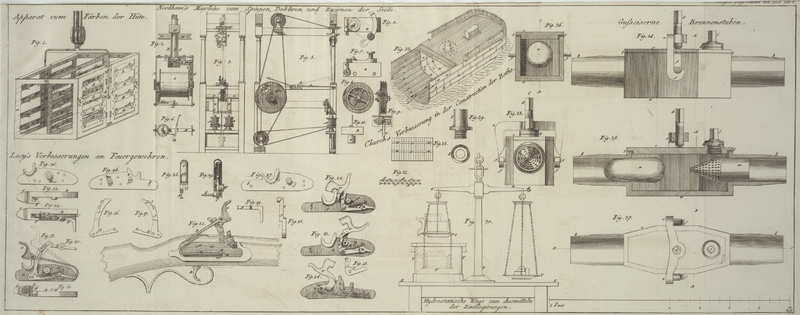
Man nimmt daher eine empfindliche Wage PQR
Fig. 30,
deren Balken wenigstens 3 Kilogramme auf jeder Seite tragen kann, ohne sich zu
biegen. Der eiserne Fuß P dieser Wage ist auf einem
starken, besonders zu diesen Operationen bestimmten Tisch K,
L befestigt, auf welchen man das Gefaͤß V,
V stellt, welches so groß seyn muß, daß man darin die groͤßten
zinnernen Gegenstande aufhangen kann, ohne daß sie die Waͤnde
beruͤhren. Das Gefaͤß V, V ist zu diesem
Ende unter den Arm Q der Wage gestellt. Die Schalen
dieser Wage sind nicht auf gleiche Weise aufgehaͤngt. Die Schale T haͤngt an dem Arm R
wie gewoͤhnlich in geringer Entfernung von dem Tische, aber die Schale S muß so hoch uͤber dem Gefaͤße V, V haͤngen, daß sie das Wasser in diesem
lezteren nicht beruͤhrt. Am Rand dieser Schale S
sind in gleichen Entfernungen drei Ketten von Messingdraht mit langen Maschen
angebracht, um eine andere Schale U zu halten, die aus
mehreren gekreuzten Messingdrahten besteht. In diese zweite Schale kommt der
Gegenstand, welcher probirt werden soll (in der Zeichnung ist es ein Maß fuͤr
Fluͤssigkeiten, eine Kanne). Nachdem er naͤmlich vorher auf der Schale
S in der Luft gewogen wurde, fuͤllt man das
Gefaͤß V, V, um ihn im Wasser zu wiegen, mit
Wasser fast ganz voll; die Schale U muß mit dem
Gegenstande immer ganz in das Wasser tauchen. Man muß sich zu diesen Operationen wo
moͤglich des destillirten Wassers, oder doch wenigstens filtrirten
Fluß- oder Regenwassers bedienen. Auch muß man genaue Gewichte haben, welche
bis auf einen halben Centigramm gehen.
Nachdem Alles vorgerichtet ist, legt man die Kanne, welche man probiren will, in die
Schale S und in die entgegengesezte Schale so viele
Stuͤke von Blei oder anderem Metall, daß das Gleichgewicht hergestellt wird.
Hierauf nimmt man die Kanne von der Schale und ersezt sie durch Gewichte, deren
Summe das Gewicht der Kanne in der Luft darstellt: wir wollen dieses Gewicht A nennen.
Man bringt sodann die Kanne in das Wasser im Gefaͤße V,
V und legt sie in die Schale U, so daß sie in
dem Wasser ganz untertaucht. Alsdann muß man von der Schale S so viele Gewichte wegnehmen, daß das Gleichgewicht wieder hergestellt
wird; die zuruͤkbleibenden sind die Differenz zwischen ihrem Gewicht in der
Luft und ihrem Gewicht im Wasser, und zeigen somit an, wie viel die Kanne von ihrem
Gewicht im Wasser verloren hat: wir wollen diesen Gewichtsverlust P nennen.
Man muß nun wissen, in welchem Verhaͤltniß das Gewicht P, welches die Kanne im Wasser verlor, zu dem Gewicht A, welches sie in der Luft hatte, steht. Wenn die Zahl
P 1288 Zehntausendtheils, oder bloß 129
Tausendtheile von A uͤberschreitet, ist der
Gehalt gut; ist sie kleiner, so ist der Gehalt zu gering. Das einfachste Verfahren,
um unmittelbar zu erfahren, wie vielen Tausendtheilen des in der Luft gefundenen
Gewichtes der Gewichtsverlust im Wasser entspricht/ bestuͤnde darin, diese
leztere Zahl durch die erste, also P durch A. zu
dividiren. So einfach diese Operation ist, so hat man doch, um die Arbeit
abzukuͤrzen, die nachfolgende Tabelle berechnet, wodurch alle diese
Berechnungen in bloße Additionen verwandelt werden.
Tabelle um zu erfahren, wie viel das mit Blei legirte Zinn von
dem Gewicht, welches es in der Luft hat, im Wasser verlieren muß, wenn es 82
Procent reines Zinn enthaͤlt.
Gewicht inder
Luft.
Verlust im Wasser.
Gewicht inder
Luft.
Verlust im Wasser.
1
0,129
400
51,513
2
0,0258
500
64,392
3
0,388
600
77,270
4
0,515
700
90,148
5
0,644
800
103,026
6
0,773
900
115,905
7
0,901
1000
128,788
8
1,030
2000
257,566
9
1,159
3000
386,349
10
1,288
4000
515,132
20
2,576
5000
643,915
30
3,863
6000
772,698
40
5,151
7000
901,481
50
6,439
8000
1030,264
60
7,727
9000
1159,047
70
9,015
10000
1287,83
80
10,303
20000
2575,66
90
11,590
30000
3863,49
100
12,878
40000
5151,32
200
25,757
50000
6439,15
300
38,635
60000
7726,98
Gewicht inder
Luft.
Verlust im Wasser.
Gewicht inder
Luft.
Verlust im Wasser.
7000
9014,81
50000
64391,5
8000
10302,64
60000
77268,8
9000
11590,47
70000
90148,1
10000
12878,3
80000
103026,4
20000
25756,6
90000
115704,7
30000
38634,9
100000
128783.
40000
51513,2
Die Anwendung dieser Tabelle ist sehr einfach, wie man aus folgenden beiden
Beispielen ersieht.
Erstes Beispiel. Wenn man das Gewicht eines zinnernen
Gefaͤßes in der Luft gleich 7325 Grammen findet, so nimmt man in der
Tabelle
Fuͤr
7000
901,481
– 300
38,635
– 20
2,576
–
5
0,644
–––––––
Die Addition ergibt als Summe
943,336
Dieß ist nun der Gewichtsverlust, welchen das Gefaͤß im Wasser erleiden muß;
verliert es darin mehr, so enthaͤlt es mehr als 82 Procent reines Zinn;
verliert es weniger, so ist dieß ein Beweis, daß die Legirung nicht genug Zinn
enthaͤlt. Man bringt also das Gefaͤß in Wasser, zaͤhlt die
Gewichte, welche in der Schale geblieben sind und wenn sich diese Gewichte z.B. zu
943,4 Gr. oder 944,6 Gr. ergeben, welche Zahlen groͤßer sind als 943,336, so
schließt man daraus, daß der Gehalt gut ist; betraͤgt der Gewichtsverlust nur
943,3, so enthielte die Legirung zu wenig Zinn.
Zweites Beispiel. Man finde das Gewicht eines
Gefaͤßes in der Luft zu 8549 Decigrammen; so nimmt man in der Tabelle:
Fuͤr
8000
1030,264
– 500
64,392
– 40
5,151
–
9
1,159
––––––––
Summe
1100,966
Dieß wird die Anzahl von Decigrammen seyn, welche das Gefaͤß im Wasser
verlieren muß, wenn sein Zinngehalt 82 Procent betraͤgt.
Wenn die Gewichte, welche in der Schale 8 nach dem Abwaͤgen in Wasser bleiben,
1100,966 uͤberschreiten, so ist der Gehalt gut; wenn hingegen die Summe
dieser Gewichte kleiner ist, so ist er zu gering: auf diese Art kann man also leicht
finden, ob ein zinnernes Gefaͤß der Gesundheit nachtheilig ist, oder
nicht.
Tafeln