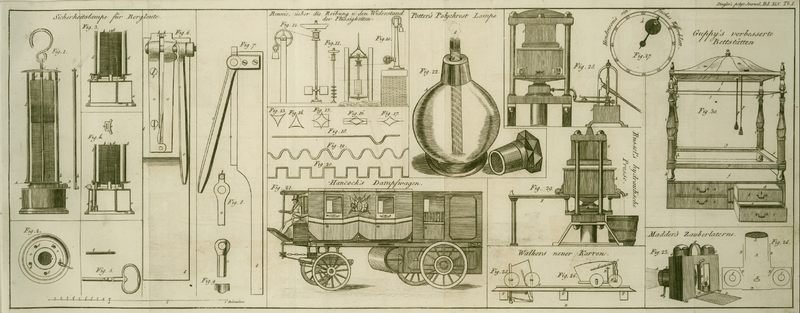
| Titel: | Ueber die Reibung und den Widerstand der Flüssigkeiten. Von Georg Rennie Esq. V. P. R. S. |
| Fundstelle: | Band 45, Jahrgang 1832, Nr. II., S. 4 |
| Download: | XML |
II.
Ueber die Reibung und den Widerstand der
Fluͤssigkeiten. Von Georg
Rennie Esq. V. P. R. S.
Vorgetragen vor der Royal
Society im Julius 1831. Aus dem London Journal of Arts. December 1831 –
Februar 1832.
Mit Abbildungen auf Tab.
I.
Rennie, uͤber die Reibung und den Widerstand der
Fluͤssigkeiten.
Ich trug der Gesellschaft schon fruͤher die Resultate mehrerer Versuche
uͤber die Reibung und den Widerstand der Oberflaͤchen fester
Koͤrper vor,Siehe Polytechn. Journal Bd. XXXIV. S.
95. und bemerkte schon damals, daß dieselben nur einen Theil der Versuche
bildeten, die ich uͤber die Reibung im Allgemeinen anstellte und noch ferner
anstellen wollte. Ich machte es mir Anfangs zur Aufgabe das Verhaͤltniß zu
erforschen, welches zwischen der Verspaͤtung oder Aufhaltung, die durch die
Bewegung der Oberflaͤchen zweier fester Koͤrper auf einander entsteht,
und zwischen jener Verspaͤtung besteht, die in Folge der Reibung fester
Koͤrper auf Fluͤssigkeiten Statt findet. Da ich jedoch fand, daß schon
der erstere dieser bilden Gegenstaͤnde eine Abhandlung von bedeutender
Ausdehnung gab, so verschob ich lezteren bis zu einer anderen Gelegenheit. Die in
meiner fruͤheren Abhandlung gegebenen Versuche zeigten, daß die Reibung
(innerhalb der Graͤnzen der Abnuͤzung) fuͤr alle festen
Koͤrper gleich ist, und daß dieselbe weder durch die Oberflaͤche noch
durch die Geschwindigkeit geaͤndert wird. Spaͤtere Versuche mit
rollenden Koͤrpern von bedeutender Schwere und Groͤße, wobei der
Widerstand auf 1/1000 der Masse und die Oberflaͤchen im Verhaͤltnisse
von 13 zu 1 vermindert wurden, haben die Aehnlichkeit, welche zwischen dem
Widerstaͤnde von rollenden und gleitenden Koͤrpern Statt findet,
bestaͤttiget. Auf diese Weise entstanden durch die Verbindung und Fortsezung
der einzelnen Versuche Coulomb's und Vince's, und dadurch, daß den abnuͤzenden
Widerstaͤnden der vorzuͤglichsten und gebraͤuchlichsten festen
Koͤrper ein sicherer Werth angewiesen wurde, bedeutende und wichtige
Fortschritte in der Wissenschaft.
Der Gegenstand dieser Abhandlung bringt jedoch groͤßere und complicirtere
Schwierigkeiten mit sich. Die Theorie der festen Koͤrper, so wie sie sich aus
den Gesezen der Mechanik ergibt, laͤßt sich, unabhaͤngig von
Versuchen, auf alle Arten dieser Koͤrper anwenden; allein die Theorie der
Fluͤssigkeiten, bei welchen die Form und Einrichtung der Theilchen, so wie
die Geseze ihrer Wirkung unbekannt sind, muß sich nothwendig auf Versuche
gruͤnden; und selbst mit dieser Huͤlfe, die wir auch nur durch
Dazwischenkunft eines festen Koͤrpers erhalten koͤnnen, muß unsere
Kenntniß von den wahren Eigenschaften der Fluͤssigkeiten noch schwankend und
ungewiß bleiben. Wir fanden daher auch, daß die Hydrostatik in den beiden lezten
Jahrhunderten die Aufmerksamkeit mehrerer der ausgezeichnetsten Mathematiker und
Physiker auf sich zog, und zwar vom J. 1628 an, in welchem Castelli zuerst seine Abhandlung uͤber das Messen des fließenden
Wassers bekannt machte, bis zu den hydraulischen Forschungen Eytelweins und Young's. Sowohl Frankreich, als
Deutschland und England haben im Verlaufe dieser Zeit das Ihrige zur
Foͤrderung der Wissenschaft beigetragen; den Italienern jedoch verdanken wir
vor Allen die Begruͤndung derselben durch die zahlreichen Forschungen und
Controversen, zu welchen die Fluͤsse Italiens Veranlassung gaben. Hieher
gehoͤren die Schriften Castelli's, Viviani's,
Zendrini's, Manfredi's, Polini's, Frisi's, Guilelmini's, Lechi's,
Michellotti's und vieler anderer.
Jeder dieser Auctoren versuchte, im Allgemeinen mit verschiedenem Gluͤke, eine
Theorie aufzustellen, welche auf Fluͤsse und Stroͤme anwendbar
waͤre. Neuen Zuwachs erhielt die Wissenschaft jedoch durch die Forschungen
Bossut's, Dubuat's, Venturi's, Funck's, Brunning's, Bidone's, Coulomb's, Prony's, Eytelwein's und
Girard's, und in England durch M'Claurin, Vince, Matth. Young, Dr.
Jurin, Prof. Robinson und den sel. Dr. Thom. Young. Sir Isaac Newton erwies bereits in den beruͤhmten
Saͤzen 51, 52 und 53 der Principia (bei dem Falle, in welchem ein sich
bewegender Cylinder in eine Fluͤssigkeit untergetaucht ist), daß der
Widerstand, welcher durch den Mangel einer vollkommenen Schluͤpfrigkeit der
Fluͤssigkeiten entsteht (caeteris paribus) mit
der Geschwindigkeit im Verhaͤltnisse sieht, mit welcher die Theile der
Fluͤssigkeit von einander getrennt werden; und daß, wenn sich ein fester
Cylinder von unendlicher Laͤnge mit gleichfoͤrmiger Bewegung in einer
gleichfoͤrmigen und unendlichen Fluͤssigkeit um eine feststehende
Achse dreht, die periodischen Zeiten, bei welchen die Theile der Fluͤssigkeit
auf diese Weise in Bewegung gesezt werden, mit den Entfernungen derselben von der
Achse im Verhaͤltnisse stehen. Diese Theorie wurde, obschon sie sich mit dem
Versuche gut vertrug, von Bernoulli und d'Alembert verworfen, und zwar aus dem Grunde, weil Newton die Centrifugalkraft oder die Reibung nicht in
Anschlag brachte, welche durch den Druk der concentrischen Ringe oder Faden um den
Cylinder entsteht, wobei die Fluͤssigkeit als stillstehend und die Reibung
der Ringe als durchaus gleichmaͤßig angenommen wuͤrde.
Pitot (1728) war der erste, welcher durch seine Versuche
an den Wasserwerken zu
Marly und Versailles erwies, daß, bei gleichen Schnelligkeiten und im
Verhaͤltnisse des Volumens des Wassers, die Reibung des Wassers in
Roͤhren in umgekehrtem Verhaͤltnisse zu dem Durchmesser dieser
Roͤhren steht. Couplet (1733), Mariotte und Deparcieux
ermittelten den Unterschied, welcher zwischen den wirklichen und berechneten Mengen,
die glaͤserne und andere Rohren liefern, besteht.
Chezy (im J. 1771 und 1786) war der erste, der das
Verhaͤltniß auszumitteln suchte, welches zwischen der Neigung einer
Wasserleitung und dem Querdurchschnitte des Volumens Wasser, welches dieselbe fuhren
soll. Statt findet; – in der Voraussezung, daß die beschleunigende oder
treibende Kraft, die von der Neigung des Bettes der Wasserleitung herruͤhrt,
durch den Widerstand des Canales im Verhaͤltnisse der Oberflaͤche
aufgewogen wird, und im Verhaͤltnisse zu dem Quadrate der Geschwindigkeit
zunimmt. Was Chezy angedeutet hatte, wurde von Bossut zu Ende gebracht; dieser entfernte naͤmlich
alle weiteren Schwierigkeiten aus der Untersuchung, und bewies, daß sich dieselbe
mit der Theorie vertruͤge. Er fand, daß sich durch kleine Oeffnungen wegen
der groͤßeren Reibung verhaͤltnißmaͤßig weniger Wasser
entleert, als durch groͤßere; daß sich die Vena
contracta und die daraus resultirende entleerte Menge mit der Hoͤhe
des Behaͤlters vermindere; er mittelte das Gesez aus, nach welchem die
Entleerung nach der Neigung und der Zahl der Kruͤmmungen einer Roͤhre
abnimmt, so wie den Einfluß der Reibung auf die Verzoͤgerung oder auf das
Aufhalten der Bewegung des Wassers in Canaͤlen und Roͤhren, an denen
er das Quadrat der Geschwindigkeit in umgekehrtes Verhaͤltniß zu der
Laͤnge der Roͤhre brachte. Er bestimmte die Coefficienten durch
Versuche, und erhielt auf diese Weise eine Formel, welche die Bedingungen zur
gleichfoͤrmigen Bewegung des Wassers in offenen Canaͤlen
ausdruͤkte. Der groͤßere Theil dieser Hypothesen wurde durch die
ausgebreiteten Untersuchungen Dubuat's noch weiter
ausgedehnt. Das große hydraulische Werk, welches derselbe in den Jahren 1779 und
1786 herausgab, enthaͤlt viele aͤußerst schaͤzbare
Beobachtungen, deren Resultat ziemlich genau mit der neuen Formel fuͤr die
Bewegung des Wassers in Roͤhren und offenen Wasserleitungen
uͤbereinkommt. Die Versuche, die er mit Roͤhren, die in verschiedenen
Winkeln, von 1/40000 eines rechten Winkels bis zu 90 Graden, und in Canaͤlen
von 1 1/2 Linien im Durchmesser bis zu einem Flaͤcheninhalte von 7–8
Quadratklafter anstellte, scheinen jeden moͤglichen Fall in sich zu fassen.
Er erhielt daher durch das Sammeln einer ungeheuren Zahl von Thatsachen, die sich
auf comprimirbare und nicht comprimirbare Fluͤssigkeiten bezogen, einen
allgemeinen Ausdruk
fuͤr alle die Faͤlle, welche sich auf die Reibung und die
Cohaͤsion der Fluͤssigkeiten beziehen koͤnnen. In diesen
Ausdruk brachte er jedoch eine logarithmische Function, durch die derselbe einen
etwas unbestimmten Charakter erhielt, welcher dessen Anwendung beschraͤnkte
und die Notwendigkeit neuer Nachforschungen bewies. Ventruri wiederholte im Jahr 1798 die Versuche Bossut's uͤber die Menge Fluͤssigkeit, welche verschieden
geformte Oeffnungen und Roͤhren geben, und besonders uͤber die
seitliche Mittheilung der Bewegung durch die Cohaͤsion der
Fluͤssigkeiten, und vermehrte dieselben in seinem Werke: „Sur la communication latérale du mouvement dans
les fluides“ mehrere neue Thatsachen. Coulomb
naͤherte sich der Aufloͤsung der Frage durch einen sehr sinnreichen
Apparat, welcher aus Scheiben von verschiedener Groͤße bestand, die an ihrem
Mittelpunkte an dem unteren Ende eines Messingdrahtes befestigt waren, und die durch
die Kraft der Drehung allein in den Fluͤssigkeiten zum Schwingen gebracht
wurden. Er schloß aus seinen Versuchen, daß der Widerstand eine aus zwei
Ausdruͤken zusammengesezte Function ist, von denen der eine mit der ersten,
der andere mit der zweiten Kraft des Widerstandes im Verhaͤltnisse sieht;
ferner, daß dieselbe durch die vermehrte Hoͤhe der Fluͤssigkeit nicht
merklich zunimmt, sondern bloß durch die Cohaͤsion der Theilchen der
Fluͤssigkeit, welche im Verhaͤltnisse zu ihrer Klebrigkeit mehr oder
weniger Widerstand darbietet, wobei sich das Oehl zum Wasser, wie 17,5 zu 1
verhaͤlt. Zu welchen Schluͤssen uͤbrigens Coulomb gelangt seyn mochte, so ist so viel gewiß, daß sowohl die
Groͤße als die Einrichtung seines Apparates nicht fuͤr die Erreichung
von Resultaten berechnet ist, auf die sich eine genuͤgende Theorie bauen
ließe. Die HH. Prony und Girard haben daher auch bei ihren Formeln des Widerstandes nicht die
Formel Coulomb's angenommen, sondern das Mittel der
besten, von anderen Auctoren angestellter Versuche. Da jedoch diese Formeln bloß die
mittlere Geschwindigkeit angeben, welche viel bedeutender ist, als die
Geschwindigkeit der Fluͤssigkeit, die an die Roͤhre graͤnzt,
welche allein in den Ausdruk der verspaͤtenden oder aufhaltenden Kraft kommen
muß, so folgt hieraus, daß die Coëfficienten, die aus dem Mittel aller der,
von diesen Maͤnnern angenommenen Versuche berechnet sind, einen weit
geringeren Werth als die Bewegung jener Fluͤssigkeit haben, welche mit den
Waͤnden der Roͤhre oder der Wasserleitung in Beruͤhrung stehen.
Um nun den Werth dieser Art von Widerstand genau zu bestimmen, machte Hr. Girard (siehe Mémoirs des
Savans étrangers 1815) eine ungeheuere Menge von Versuchen mit
Roͤhren von verschiedenem Durchmesser und verschiedener Laͤnge, aus
welchen Versuchen er den Schluß zog, daß sich die Verspaͤtung wie die einfache Geschwindigkeit
verhaͤlt. Die Wirkungen der Temperatur sind hiebei sehr merkwuͤrdig;
wenn naͤmlich die Geschwindigkeit bei 0° des 100gradigen Thermometers
10 betraͤgt, so wird sie bei einer Temperatur von 85° das Vierfache
oder 42 betragen: diese Werthe sind uͤbrigens nicht ganz genau, sondern
muͤssen bloß als Annaͤherungen zur Wahrheit angesehen werden.
Die Entdekungen, mit welchen die brittischen Gelehrten diese Wissenschaft
bereicherten, sind leider nur sehr spaͤrlich; denn außer Newton, der eigentlich die Bahn brach, Dr. Jurin, Dr. Matth. Young,
Dr. Desaguliers, Dr. Vince,
Smeaton, Banks und dem seligen Dr. Thom. Young
hat beinahe Niemand bei uns Versuche uͤber diesen Gegenstand gemacht. Alles
was unsere Mechaniker und Gelehrten leisteten, wurde entweder gar nicht
oͤffentlich bekannt, oder zur Vergessenheit verdammt, und obschon wir
Suͤmpfe und Moraste von mehreren tausend Aekern haben, so besizen wir
uͤber das Trokenlegen derselben und das Ableiten des
uͤberfluͤssigen Wassers doch nur Abhandlungen und Berichte von rein
oͤrtlichem Interesse, die fuͤr die Hydraulik im Allgemeinen nur von
geringer Wichtigkeit sind.
Aus dieser kurzen und unvollstaͤndigen geschichtlichen Darstellung geht
hervor, daß bereits Vieles zur Vervollkommnung dieser Wissenschaft gethan wurde.
Ebenso gewiß ist aber, daß noch Vieles zu thun uͤbrig ist. Obschon wir den
franzoͤsischen und englischen Physikern großen Dank fuͤr ihre
Forschungen uͤber die Geseze der Capillar-Attraction schuldig sind, so
bleiben doch noch die Adhaͤsion der Fluͤssigkeiten an Metallscheiben,
die Phaͤnomene der Fluiditaͤt und die Geseze, nach welchen sich die
Bewegung und das Gleichgewicht der Theilchen der Fluͤssigkeiten richtet, eine
rein geometrische Aufgabe. Da wir nun aber keine anderen Mittel, als die
Dazwischenkunft eines festen Koͤrpers besizen, um zur Loͤsung dieser
Aufgaben zu gelangen so muͤssen wir uns einstweilen mit den unvollkommenen
Formeln begnuͤgen, die aus den Versuchen, welche in kleinem Maßstabe
uͤber die Reibung und Adhaͤsion des Wassers in Roͤhren und
Wasserleitungen angestellt worden, berechnet wurden, bis wir einst die Ursache: der
Verspaͤtungen oder der aufhaltenden Kraft an den Fluͤssen genauer und
richtiger ermessen koͤnnen werden.
Ich schlage nun vor, bei der Untersuchung dieser Aufgabe zuerst zu bestimmen, in
welchem Maße feste Koͤrper aufgehalten oder verspaͤtet werden, deren
Oberflaͤche sich auf stillstehenden Fluͤssigkeiten bewegen; dann jene
Verspaͤtungen oder Aufhaltungen, die sich bei der Bewegung von
Fluͤssigkeiten uͤber feste Koͤrper ergeben, und drittens endlich den directen
Widerstand fester Koͤrper, die sich in stillstehenden Fluͤssigkeiten
umdrehen.
Zum Behufe der Erforschung des ersten Falles ließ ich den in Fig. 10 dargestellten
Apparat verfertigen. Derselbe besteht aus einem hoͤlzernen Cylinder von 10
3/4 Zoll im Durchmesser und 24 Zoll Laͤnge, welche Lange in 8 Abtheilungen
von 3 Zoll getheilt ist. Dieser Cylinder ist an einer eisernen Spindel von 4 Fuß
Laͤnge und 1 1/4 Zoll Dike befestigt. Der ganze Apparat war genau abgedreht
und sorgfaͤltig polirt. An dem oberen Theile der Spindel ist ein kleiner
Cylinder oder eine Rolle von 6 Zoll im Durchmesser befestigt, und um diese wurde
eine feine biegsame seidene Schnur gewunden, welche mit dem Gewichte communicirte.
Dieser Apparat nun wurde in einem eisernen Gestelle gehoͤrig befestigt, und
dieses Gestell in die zwei Fugen oder Falzen zweier aufrechter, in das Bett der
Themse eingerammter Pfosten eingesezt.
Diese Einrichtung des Gestelles wurde deßwegen getroffen, damit der Cylinder nach der
Hoͤhe der Fluch auf- und abwaͤrts gleiten konnte, und damit
sich derselbe, je nachdem es bei diesem oder jenem Versuche noͤthig war, auf
verschiedene Tiefe untertauchen ließ. Die Reibung des Apparates selbst, oder die
Zeit, welche das Gewicht brauchte, um in der Luft herabzusteigen, wurde
vorlaͤufig bemessen und aufgezeichnet. Dann wurde derselbe allmaͤhlich
3, 6, 9, 12, 15, 18, 21 und 24 Zoll tief in das Wasser untergetaucht. Die
Unterschiede in der Zeit, welche die Verspaͤtung oder Aufhaltung durch das
Wasser anzeigen, ergeben sich aus folgender Tabelle.
Versuche uͤber die Reibung der Oberflaͤche eines
Cylinders von 24 Zoll Laͤnge und 10 3/4
Zoll im Durchmesser bei seiner Bewegung in der Luft und im
Wasser.
Tab. I. Versuche uͤber Oberflaͤchen im
Wasser.
Textabbildung Bd. 45, S. 10
Tiefe der Eintauchung des
Cylinders; Angehaͤngtes Gewicht; Zahl der Umdrehungen des Cylinders
beim Herabfallen durch die ganze Hoͤhe v. 26 Fuß; Zeit beim
Herabsteigen im Wasser; Geschwindigkeit der Peripherie in der Luft per
Secunde; Unterschied zwischen den Geschwindigkeiten in der Luft und im
Wasser; Bemerkungen; Der Widerstand nahm mit der Vergroͤßerung der
Oberflaͤchen nur langsam, allein nicht im Verhaͤltnisse der
Oberflaͤchen zu; Der Widerstand wurde durch Oberflaͤchen mit
erhoͤhten Geschwindigkeiten kaum veraͤn-; Zolle; Pfund;
Secunden
Textabbildung Bd. 45, S. 11
Versuche uͤber
Geschwindigkeiten im Wasser; Zoll; Pfund; detto; Secunden; Konnte nicht
untersucht werden
Schluͤsse aus Tab. I.
1) Die Reibung oder Adhaͤsion des Wassers an den Oberflaͤchen
fester sich bewegender Koͤrper naͤhert sich dem
Verhaͤltnisse der Oberflaͤchen bei langsamen Geschwindigkeiten;
allein eine Vergroͤßerung der Oberflaͤche hat bei vermehrten
Geschwindigkeiten keinen wesentlichen Einfluß auf dieselbe.
2) Bei gleichen Oberflaͤchen scheinen die Geschwindigkeiten kein
bestimmtes Verhaͤltniß zu beobachten, jedoch scheint sich dieses
Verhaͤltniß den Quadraten des Widerstandes zu naͤhern.
Bei vermehrten Geschwindigkeiten zeigte sich der Index der Kraft niedriger als
das gedoppelte Verhaͤltniß.
––––––––––
Um diese Schluͤsse auch auf eine andere Weise zu bestaͤtigen, wurde
der Cylinder entfernt, und dafuͤr, wie man in Fig. 11 sieht,
kreisfoͤrmige eiserne Scheiben von 10 3/4 Zoll Durchmesser und 1/8 Zoll
Dike genau an der Spindel befestigt und polirt. Mit diesem Apparate nun wurde
gleichfalls auf die obige Weise durch Untertauchen desselben unter die Themse
die Reibung untersucht.
II. Tabelle.Versuche uͤber die Reibung im Wasser, welche bei
kreisfoͤrmigen Scheiben von 10 3/4 Zoll im
Durchmesser und 1/8 Zoll Dike Statt findet, wenn
diese Scheiben 6 Zoll weit von einander entfernt sind, und sich parallel mit
dem Horizonte umdrehen.
Textabbildung Bd. 45, S. 12
Zahl der Scheiben;
Angehaͤngtes Gewicht; Hoͤhe, durch welche das Gewicht
faͤllt; Zeit des Herabsteigens des Gewichtes im Wasser;
Geschwindigkeit des Umfanges per Secunde; Zeit des Herabsteigens des
Gewichtes in der Luft; Geschwindigkeit des Umfanges per Secunde in der Luft;
Unterschied; Pfund; Secunden; Zolle
Textabbildung Bd. 45, S. 13
Schluͤsse aus Tab. II.
Die Reibung oder Adhaͤsion des Wassers verhaͤlt sich bei geringen
Geschwindigkeiten nicht ganz wie die Oberflaͤchen, wobei das
Verhaͤltniß wie 1 zu 3 statt wie 1 zu 4 ist, sondern sie vermindert sich
sehr schnell, und zwar ohne irgend ein Verhaͤltniß bei zunehmenden
Geschwindigkeiten zu beobachten.Die Versuche der Society for the Improvement of
Naval Architecture zeigten bei erhoͤhten
Geschwindigkeiten einen verminderten Widerstand. A. d. O. Hieraus folgt, daß der Widerstand eines Schiffes, welches sich mit einer
mittleren oder hoͤheren Geschwindigkeit bewegt, einen unbedeutenden Theil
jenes Widerstandes bildet, der dadurch entsteht, daß die Fluͤssigkeit aus
der Stelle getrieben wird, und daß die Glaͤtte des Kupfers, welche man an
Schiffen nach einer zuruͤkgelegten Reise beobachtet, von anderen
Ursachen, als von der Reibung allein herruͤhren muß.
––––––––––
Ich machte einen Versuch, um vergleichsweise den Widerstand auszumitteln, welcher
Statt findet, wenn sich eine Roͤhre in Wasser umdreht, und wenn Wasser
durch die Roͤhre laͤuft. Ich fand hiebei, daß sich der Widerstand
bei geringen Geschwindigkeiten wie die Oberflaͤchen verhielt, daß er sich
aber bei groͤßeren Geschwindigkeiten auf die oben erwaͤhnte Weise
bedeutend verminderte, und zwar ohne dabei ein bestimmtes Verhaͤltniß zu
beobachten.
Obige Schluͤsse oder Folgerungen aus den Versuchen stehen mit jenen Coulomb's im Widerspruche, indem dieser nicht gefunden haben will,
daß Druk den Widerstand vermehre, sondern behauptet, daß der Widerstand
groͤßer ist, wenn die Untertauchung nur partiell Statt findet.
Da sich der Apparat auf Fluͤssigkeiten im Allgemeinen anwenden
laͤßt, so; benuzte ich denselben auch um den directen Widerstand fester
Koͤrper gegen Fluͤssigkeiten auszumitteln,In diesem Falle wird die Zahl der Theilchen, welche getroffen werden, im
Verhaͤltnisse des Radius zu dem Sinus der Neigung abnehmen und
daher wird sich der Widerstand in dem doppelten Verhaͤltnisse des
Radius zu dem Sinus der Neigung vermindern. Da jedoch die Sinus der
Neigung der beiden Platten gleich sind, so werden die
Widerstaͤnde aͤquivalent seyn der Flaͤche einer
Platte (welche sich senkrecht auf ihre Ebenen bewegt) in das doppelte
Verhaͤltniß der Geschwindigkeit ihrer Bewegung und der Dichtheit
der Fluͤssigkeit. A. d. O. indem ich Platten und Kugeln in demselben so in Umdrehung brachte, daß
deren Flaͤchen eine senkrechte Richtung gegen die Flaͤche des
Horizonts hatten. (Siehe Fig. 12.)
Obschon der Widerstand der festen Koͤrper in Fluͤssigkeiten
eigentlich nicht den Gegenstand dieser Abhandlung bildet, so muß ich doch
mehrere detaillirte Beobachtungen uͤber diese Versuche jezt schon hier
anfuͤhren, indem dieselben mit einem anderen Zweige der
Hydro-Dynamik in innigem Zusammenhange stehen. Da besonders die
Darstellung des Verhaͤltnisses zwischen den Widerstaͤnden der
Cohaͤsion und des Impulses von großer Wichtigkeit ist, so hielt ich es
fuͤr zwekmaͤßig hier folgende Versuche aufzufuͤhren.
III. Tabelle.Versuche uͤber die Umdrehungen eiserner Scheiben
und hoͤlzerner Kugeln in der Luft, und zwar in einer solchen
Stellung, daß deren Flaͤchen senkrecht mit dem Horizonte
stehen.
Textabbildung Bd. 45, S. 15
Aufgehaͤngtes Gewicht;
Fall-Hoͤhe; Zeit des Herabsinkens; Zwei kreisfoͤrmige
Scheiben von 10 3/4 Zoll im Durchmesser. Flaͤchenraum 81 Zoll;
Geschwindigkeit per Secunde; Zwei vierekige Fluͤgel.
Flaͤchenraum 81 Zoll; Zwei hoͤlzerne Kugeln von 10 3/4 Zoll im
Durchmesser; Pfund; Die Spindel machte waͤhrend eines Falles von 25
Fuß 15,9 Umdrehungen. Der mittlere Kreis von 51,83 bewegte sich durch 68,67
Fuß; Secunden; Fuß
Schluͤsse.
1) Die Widerstaͤnde verhalten sich wie die Quadrate der
Geschwindigkeiten.
2) Die Widerstaͤnde zwischen Scheiben und Kugeln verhalten sich beinahe
wie 2 zu 1.
IV. Tabelle.Versuche uͤber den Widerstand, welchen eiserne
Scheiben und hoͤlzerne Kugeln beim Umdrehen in Wasser
erleiden.
Textabbildung Bd. 45, S. 16
Gewicht;
Fall-Hoͤhe; Zeit des Herabsinkens; Zwei kreisfoͤrmige
Scheiben von 81 Zoll Flaͤchenraum; Geschwindigkeit per Secunde; Zwei
vierekige Fluͤgel jeder von 9 Quadratzoll und 81 Zoll
Flaͤchenraum; Zwei hoͤlzerne Kugeln von 81 Zoll
Flaͤchenraum; Die Spindel machte waͤhrend eines Falles von 25
Fuß 15,9 Umdrehungen. Der mittlere Kreis von 51,83 wuͤrde sich durch
824,19 Zoll oder 68,67 Fuß bewegen; Secunden; Fuß
Schluͤsse.
1) Die Widerstaͤnde sind die Quadrate der Geschwindigkeiten.
2) Die mittleren Widerstaͤnde kreisfoͤrmiger Scheiben, vierekiger
Platten und Kugeln verhalten sich in der Luft wie die Zahlen 25,180, 22,010,
10,627; und im Wasser wie die Zahlen 1,18, 1,36, 0,755; folglich sind die
proportionalen Widerstaͤnde der Luft zum Wasser
bei kreisfoͤrmigen Scheiben
wie
1 zu 21,3
bei Platten und Fluͤgeln
wie
1 zu 16,2
bei hoͤlzernen Kugeln wie
1 zu 2,2
Anmerkung. Aus den Fluͤgeln, welche man in
Fig.
12 sieht, wurde ein Theil, welcher dem vierten Theile des
Flaͤchenraumes eines jeden Fluͤgels gleichkam, ausgeschnitten,
wobei es sich zeigte, daß der Widerstand eben so groß war, als bei den
vierekigen Fluͤgeln.
Versuche uͤber die Quantitaͤten Wasser, welche
Oeffnungen und Roͤhren von verschiedenen Durchmessern und Laͤngen
bei verschiedenen Hoͤhen entleeren.
Die Phaͤnomene, welche sich auf sprizende Fluͤssigkeiten beziehen,
sind:
1) Die Ungleichheit in der Geschwindigkeit der Theilchen, welche in jedem
horizontalen, der Oeffnung parallelen Durchschnitte enthalten sind.
2) Die Zusammenziehung des Strahles der Fluͤssigkeit außer der Oeffnung und
die dadurch erfolgende Verminderung der Entleerung im Vergleiche mit der
Theorie.
3) Die Umkehrung und Veraͤnderungen in den Durchschnitten des Strahles bei
verschiedenen Entfernungen von den Oeffnungen.
Alle diese Phaͤnomene wurden bereits von verschiedenen Auctoren
eroͤrtert; auch gaben dieselben Formeln an, welche den verschiedenen
Umstaͤnden der Entleerung an Fluͤssigkeit angepaßt waren. Allein weder
Bossut noch Du Buat, die
genauesten aller Schriftsteller uͤber diesen Gegenstand, haben eine
fortlaufende und systematische Reihe von Versuchen uͤber die vergleichsweise
Entleerung von Fluͤssigkeit durch Oeffnungen und Roͤhren von
verschiedenem Flaͤcheninhalte, verschiedener Hoͤhe und Laͤnge
angegeben. Der Apparat, mit welchem ich meine Versuche anstellte, bestand aus einem
genau verfertigten hoͤlzernen Behaͤlter von 2 Fuß im Gevierte inneren
Raumes und 4 Fuß Hoͤhe. Das Wasser wurde durch einen Regulirhahn auf
bestaͤndiger gleichmaͤßiger Hoͤhe erhalten; ein Schwimmer mit
einem Zeiger sezte den Beobachter in den Stand, sich genau von der Hoͤhe zu
uͤberzeugen, auf welcher das Wasser in dem Behaͤlter uͤber dem
Mittelpunkte der Entleerungsoͤffnung stand.
Die Oeffnungen wurden durch Dollond in Messingplatten von
1/6 Zoll Dike mit aller Genauigkeit gemacht. Diese Platten wurden genau in eine
Oeffnung eingepaßt, welche sich in der Seite des Behaͤlters befand, und
mittelst einer, in jede der Platten eingeriebene Klappe verschlossen. Die Klappe
wurde durch einen Hebel geoͤffnet, und die Zeit mittelst Chronometer
gemessen.
Die Durchmesser der gezogenen Roͤhren waren so genau als moͤglich; an
den Enden der Roͤhren waren die Durchmesser sorgfaͤltig erweitert,
damit ja kein Drahtrand deren Durchschnitte vermindern konnte. Nachdem nun hiebei
das eine Ende der Roͤhre in einen, an dem Behaͤlter befestigten
Bloͤke aus hartem Holze eingesezt, und das andere mittelst einer Klappe
verschlossen worden, wurden die Versuche damit auf die angegebene Weise notirt.
V. Tabelle.Jedes Resultat ist das Mittel von vier Versuchen, A. d. O.
Textabbildung Bd. 45, S. 18
Kreisfoͤrmige Oeffnung
in einer Messingplatte von 1 Zoll im Durchmesser und 1/60 Zoll Dike;
Bestaͤndige Hoͤhe der Oberflaͤche des Wassers
uͤber dem Mittelpuncte der Oeffnung; Wirkliche Zeit zum Entleeren von
1 Kubikfuß; Theoretische Zeit zum Entleeren eines Kubikfußes;
Verhaͤltniß der theoretischen zur wirklichen Entleerung; Vena
contracta; Fuß; Secunden; Nicht genau gemessen; Kreisfoͤrmige
Oeffnung in einer Messingplatte von 3/4 Zoll-Durchmesser und 1/60
Zoll Dike; In einer Entfernung von 6/10 Zoll von der Oeffnung hatte sich der
Durchmesser auf 0,685 Zoll zusammengezogen
Textabbildung Bd. 45, S. 19
Kreisfoͤrmige Oeffnung
in einer Messingplatte von 1/2 Zoll Durchmesser und 1/60 Zoll Dike; In einer
Entfernung von 1/2 Zoll von der Oeffnung hatte sich der Durchmesser auf 0,37
Zoll zusammen; Kreisfoͤrmige Oeffnung in einer Messingplatte von 1/4
Zoll Durchmesser und 1/60 Zoll Dike; Einen Viertel Zoll außer der Oeffnung
zog sich der Durchmesser so zusammen, daß er 1/20 Zoll weniger betrug, als
die Oeffnung
Bemerkungen.
Die Phaͤnomene ruͤksichtlich der Form und Richtung des Strahles
springender Fluͤssigkeiten, und die merkwuͤrdigen
Veraͤnderungen des Wasserstrahles bei gewissen Entfernungen von den
Oeffnungen, wurden in den Experiences sur la Forme et sur
la Direction des Veins et des Courans d'eau, par
George Bidone Turin 1829, so genau und
vollstaͤndig angegeben, daß ich es unnoͤthig halte mehr
daruͤber zu sagen, als daß sie durch obige Versuche vollkommen
bestaͤttigt wurden.
Versuche uͤber die Mengen Wasser, welche durch
rechtekige und dreiekige Oeffnungen, die in Kupferplatten von 1/6 Zoll Dike und gleichem Flaͤchenraume angebracht waren,
aus einem bestaͤndig voll erhaltenen Gefaͤße und bei verschiedenen
Hoͤhen entleert wurden.
VI. Tabelle.
Textabbildung Bd. 45, S. 20
Gleichseitiges Dreiek von 1
Zoll Flaͤchenraum, mit einem Winkel nach Oben gerichtet; Hoͤhe
der Oberflaͤche uͤber dem Mittelpuncte der Oeffnung; Zeit zum
Entleeren von 1 Kubikfuß; Theoretische Zeit zum Entleeren von 1 Kubikfuß;
Verhaͤltniß der wirklichen zur theoretischen Entleerung; Form der
Oeffnung; Fuß; Secunden; Vena contracta bei 1/2 Zoll außer der Oeffnung;
allein der Strahl kehrte sich mit den Winkeln um, und in Bezug auf die
Seiten des Dreiekes dehnte sich der Strahl spaͤter aus und verlor
seine Form. Fig. 13; Gleichseitiges Dreiek wie oben mit einem Winkel nach
Unten gerichtet; Vena contracta dieselbe wie oben, nur hatte der Strahl den
Winkel nach Oben, als nach der entgegengesezten Seite, gerichtet. Fig.
14.
Textabbildung Bd. 45, S. 21
Rechtekige Oeffnung von 1
Quadrat-Zoll; Vena contracta beilaͤufig 3/4 Zoll außerhalb der
Oeffnung, wo an die Stelle einer jeden Seite des Rechtekes ein Winkel trat,
und der Strahl sich in Schaum zertheilte. Fig. 15;
Rechtekige Oeffnung von 2 Zoll Lange, 1/2 Zoll Breite, deren laͤngere
Seite parallel mit der Oberflaͤche des Wassers lief; Vena contracta
wie im vorhergehenden Falle. An die Stelle einer jeden Seite des Rechtekes
des Strahles trat ein Winkel. Fig. 16;
Rechtekige Oeffnung von 1 1/2 Zoll Laͤnge und 5/8 Zoll Breite, in
derselben Richtung, wie im vorgehenden Falle; Vena contracta, wie vorher.
Fig.
17.
Bemerkungen.
Bei gleichem Flaͤcheninhalte ist die Menge Fluͤssigkeit, welche
durch verschiedene Oeffnungen, sie moͤgen kreisfoͤrmig, rechtekig
oder dreiekig seyn, entleert wird, beinahe gleich; die geringe Vermehrung
spricht zu Gunsten der rechtekigen Oeffnungen.
VII. Tabelle.
Versuche uͤber die Quantitaͤt Wasser, welche
bei cylindrischen glaͤsernen Oeffnungen und Roͤhren von 1 Zoll
bis zu 1 Fuß Laͤnge und von verschiedenen Durchmessern, aus einem
Gefaͤße entleert wird, welches bestaͤndig voll und auf
verschiedener Hoͤhe erhalten wird.
Textabbildung Bd. 45, S. 22
Hoͤhe der
Oberflaͤche des Wassers uͤber dem Mittelpunkte der Oeffnung;
Fuß; Zeit zum Entleeren von 1 Kubikfuß in Secunden; Zoll; Bemerkungen;
Vergleicht man diese Versuche mit der Zeit und Menge, welche aus den
Oeffnungen in den Platten entleert wurde, so ergibt sich eine Verminderung
der Zeit und eine Vermehrung des Entleerten im Verhaͤltnisse von 1/5
zu 1/4; Aus Glasroͤhren von 1 Fuß Laͤnge; Hieraus ergibt sich
eine Zunahme an Zeit und eine Verminderung der entleerten Menge im
Verhaͤltnisse von 1/2 zu 3/4.
Schluͤsse.
1) Die Mengen, welche in gleichen Zeiten aus Oeffnungen und Ansazroͤhren
entleert werden, verhalten sich wie die Flaͤchenraͤume der
Oeffnungen.
2) Die Mengen, welche sich in gleichen Zeiten aus denselben Ansazroͤhren
und Oeffnungen bei verschiedenen Hoͤhen entleerten, verhalten sich
beinahe wie die Quadratwurzeln der entsprechenden Hoͤhen.
3) Die Mengen, welche in gleichen Zeiten aus verschiedenen Ansazroͤhren
und Oeffnungen bei verschiedenen Hoͤhen entleert wurden, stehen zu
einander in dem zusammengesezten Verhaͤltnisse des
Flaͤcheninhaltes der Oeffnungen und der Quadratwurzeln der
Hoͤhen.
Nach den vorhergehenden Versuchen betraͤgt der mittlere Coëfficient
fuͤr Hoͤhen von
4 Fuß bei kreisfoͤrmigen
Oeffnungen
0,621
bei einer Hoͤhe von 1 Fuß
hingegen
0,645
bei
dreiekigen Oeffnungen und 4 Fuß
Hoͤhe
0,593
bei
dreiekigen Oeffnungen und 1 Fuß
Hoͤhe
0,596
bei rechtekigen Oeffnungen und 4 Fuß
Hoͤhe
0,593
bei rechtekigen Oeffnungen und 1 Fuß
Hoͤhe
0,616
Man kann mithin, wenn man die Ungenauigkeiten, die sich bei derlei Versuchen
nicht ganz vermeiden lassen, in Anschlag bringt, getrost die
Coëfficienten der HH. Crony und Bossut annehmen, d.h.
fuͤr Hoͤhen von 4
Fuß
0,621
fuͤr Hoͤhen von 1
Fuß
0,619
Bei den glaͤsernen Ansazroͤhren ist der Coëfficient viel
hoͤher, als jener Bossut's, indem er
fuͤr 4 Fuß 0,806 und fuͤr 1 Fuß 0,817 betrug.
Bemerkung.
Siehe Venturi's und Eytelwein's Versuche.
Es sey
A = dem
Flaͤcheninhalte der Oeffnung in Quadratfußen.
D = dem
Durchmesser der Oeffnung, wenn dieselbe kreisfoͤrmig ist.
H = der
Hoͤhe der Fluͤssigkeit in Fußen,
F = der Zeit
G die Gravitaͤt in einer
Secunde.
Nach Bossut's Versuchen ist Q = 0,61938 at√(2 gH). Da nun g eine
sich gleich bleibende Groͤße und = 7,77125 ist, so erhaͤlt man Q = 4,818 AT√H fuͤr Oeffnungen von
jeder Form, indem man d substituirt, wenn sie
kreisfoͤrmig ist, oder Q = 3,7842 d²T√H.
Aus der zweiten Formel erhaͤlt man
Textabbildung Bd. 45, S. 24
Fuͤr die Ansazroͤhren wird sich hingegen folgende Gleichung
ergeben: Q = 081 AT √(2gH
); da aber 2 g bestaͤndig und = 7,77125
ist, so erhaͤlt man Q = 4,9438 d² T √H,
woraus sich ergibt:
Textabbildung Bd. 45, S. 24
VIII. Tabelle.
Versuche uͤber die Reibung oder die Menge des
Wassers, welche durch bleierne Roͤhren von verschiedenem Durchmesser
und verschiedener Laͤnge aus einem bestaͤndig voll erhaltenen
Gefaͤße bei verschiedenen Hoͤhen entleert wird.
Gerade Roͤhren von 15 Fuß
Laͤnge.
Textabbildung Bd. 45, S. 25
Hoͤhe der
Wasserflaͤche uͤber dem Mittelpunkte der Roͤhre; Zeit
zum Entleeren vom 1 Kubikfuß; Zoll; Bleierne Roͤhren von 1/4 Zoll im
Lichten waren; Fuß; Secunden; Bemerkungen; Die Zeit zum Entleeren von 1
Kubikfuß ist beinahe doppelt so groß als die Zeit, welche bei
Glasroͤhren von gleicher Laͤnge und gleichem Durchmesser hiezu
noͤthig ist
IX. Tabelle.
Versuche uͤber die Wassermengen, welche durch
bleierne Roͤhren von 1/2 Zoll im Lichten,
und von 1 bis 30 Fuß Laͤnge entleert
werden.
Textabbildung Bd. 45, S. 26
Glaͤserne Roͤhren
von 1 Zoll Laͤnge und 1/2 Zoll Durchmesser; Messingene Oeffnung von
1/2 Zoll Durchmesser; 1 Fuß Laͤnge; 3 Fuß 9 Zoll; 7 Fuß 6 Zoll; 11
Fuß 3 Zoll; 15 Fuß; 30 Fuß; Secunden
Bemerkungen.
Das Verhaͤltniß der Entleerung bei Glasroͤhren mit Roͤhren
von 30 Fuß Laͤnge ist beilaͤufig wie 1 zu 4 – –
–; bei messingenen Oeffnungen hingegen beilaͤufig wie 1 zu 3
– – –.
Schluͤsse uͤber die Roͤhren von
verschiedener Laͤnge.
Die Wassermengen, welche aus Roͤhren von gleichem Durchmesser, aber
ungleicher Laͤnge, bei verschiedener Hoͤhe entleert werden, stehen
beinahe in folgendem Verhaͤltnisse:
Wenn sich die
Laͤngen wie
30 zu 1
verhalten, so
verhalten sich die
entleerten
Wassermengen wie
3,7 zu 1
–
–
8 zu 1
–
–
–
–
2,6 zu 1
–
–
4 zu 1
–
–
–
–
2 zu 1
–
–
2 zu 1
–
–
–
–
1,4 zu 1
Die durch glaͤserne und bleierne Roͤhren entleerten Mengen sind
beinahe gleich. Die Laͤnge einer Roͤhre kann um 3 bis 4 Fuß
erhoͤht werden, ohne daß dadurch die Entleerung im Vergleiche mit den
Platten-Oeffnungen vermindert wird.
X. Tabelle.
Die gerade Roͤhre von 1/2 Zoll im Lichten, mit welcher die vorhergehenden
Versuche angestellt wurden, wurde sorgfaͤltig in eine, in zwei, und in
vierzehn halbkreisfoͤrmige Kruͤmmungen gebogen, von denen jede 7
1/2 Zoll im halben Durchmesser hatte, und zwei den vierten Theil eines Kreises
von Radien von 3 1/6 Zoll betrugen. Das eine Ende der Roͤhre wurde, wie
fruͤher, in der hoͤlzernen Oeffnung befestigt; hiebei ergaben sich
folgende Resultate.
Roͤhre von 15 Fuß Laͤnge, 1/2 Zoll im
Lichten, mit einer halbkreisfoͤrmigen und zwei Kruͤmmungen von
1/4 Kreis.Fig.
18.
Textabbildung Bd. 45, S. 27
Hoͤhe der
Oberflaͤche des Wassers uͤber dem Mittelpunkte der Oeffnung;
Fuß; Zeit zum Entleeren von 1 Kubikfuß durch eine Roͤhre mit 3
Kruͤmmungen; Secunden; Zeit zum Entleeren von 1 Kubikfuß durch eine
gerade Roͤhre; Bemerkungen; Die Stellung der Kruͤmmungen mag
senkrecht oder wagerecht seyn, und sie moͤgen sich an dem einen oder
dem anderen Ende der Roͤhre befinden, so erleidet das Resultat keine
Veraͤnderungen dadurch
Roͤhre von 15 Fuß
Laͤnge, 1/2 Zoll im Lichten mit 14
halbkreisfoͤrmigen und zwei Kruͤmmungen
von 1/4 Kreisbogen.
Fig.
19.
Textabbildung Bd. 45, S. 28
Hoͤhe der
Oberflaͤche des Wassers uͤber dem Mittelpunkte der Oeffnung;
Fuß; Zeit zum Entleeren von 1 Kubikfuß durch eine Roͤhre mit 3
Kruͤmmungen; Secunden; Zeit zum Entleeren von 1 Kubikfuß durch eine
gerade Roͤhre; Bemerkungen; Die entleerte Menge wurde durch die
Kruͤmmungen von 1/5 bis 1/3 vermindert, woraus sich die Reibung der
Roͤhre ergibt
Resultate.
1) Bei einer halbkreisfoͤrmigen Kruͤmmung und zwei
Kruͤmmungen von 1/4 Kreisbogen weicht der Widerstand im Vergleiche mit
einer geraden Roͤhre von gleicher Laͤnge und gleicher Weite im
Lichten um 1/36 bis zu 1/70 von dem Widerstaͤnde der geraden
Roͤhre ab.
2) Bei einer Roͤhre mit 14 halbkreisfoͤrmigen und zwei
viertelkreisfoͤrmigen Kruͤmmungen weicht der Widerstand um 1/19
bis zu 1/39 von dem Widerstaͤnde einer geraden Roͤhre ab.
3) Die vermehrte Zahl der Kruͤmmungen erhoͤht den Widerstand nicht
im Verhaͤltnisse zu der Zahl der Kruͤmmungen, sondern zeigt bloß
einen vergroͤßerten Widerstand von 1/14 bis 1/35, wie sich aus einem
Vergleiche mit den 4 Kruͤmmungen ergibt.
XI. Tabelle.
Versuche uͤber die Wassermenge, welche von
bleiernen Roͤhren von 1/2 Zoll im Lichten
und 15 Fuß Laͤnge entleert wird, wenn
dieselben in 24 rechtwinkeligen Knieen, deren
Seiten 6 3/4 Zoll messen, gebogen sind.
Fig.
20.
Textabbildung Bd. 45, S. 29
Hoͤhe der
Oberflaͤche des Wassers uͤber dem Mittelpunkte der Oeffnung;
Fuß; Ein rechter Winkel S 1/2 Zoll von dem Ende der Roͤhre; Gerade
Roͤhre von 15 Fuß Laͤnge; Vier und zwanzig rechte Winkel;
Bemerkungen; Bei den drei ersten Versuchen ergibt sich eine Verminderung des
entleerten Wassers im Verhaͤltnisse von 3 zu 1 Statt
Aus den vorhergehenden Versuchen mit einer rechtwinkeligen Roͤhre
koͤnnte man schließen, daß die Verminderung der entleerten Menge sich wie
die Anzahl der rechten Winkel verhaͤlt; vergleicht man aber die
Wassermenge, welche eine Roͤhre mit einem einzigen rechten Winkel
entleert, mit jener Menge, die von einer Roͤhre mit 24 rechten Winkeln
entleert wird, so verhaͤlt sich der Unterschied beinahe nur wie 2 zu
1.
Allgemeine Bemerkungen uͤber die Wassermengen, welche
von horizontalen und gebogenen Roͤhren entleert werden.
Verschiedene Auctoren gaben bereits Formeln, welche den verschiedenen
Umstaͤnden, unter welchen sich Wasser in Roͤhren und Wasserleitungen
bewegt, angepaßt sind. Einige sind der Meinung, daß sich die Verspaͤtungen
oder Aufhaltungen umgekehrt wie die Quadrate der Langen der Roͤhren
verhalten; andere hingegen meinen, daß dieselben durch einen gewissen Theil der
Hoͤhe des Behaͤlters uͤber dem Mittelpunkte der Roͤhre
repraͤsentirt werden, indem sich der Widerstand gerade wie die Laͤnge
und der Umfang der Roͤhre, und umgekehrt wie der Flaͤcheninhalt des
Durchschnittes verhaͤlt.
Hr. Girard folgerte aus seinen schoͤnen Versuchen,
daß der Widerstand aus den ersten und zweiten Kraͤften der Geschwindigkeit
zusammengesezt ist. So daß man, wenn man die Werthe nach Dubuat's Versuchen berechnet, indem man den durch die Cohaͤsion
bewirkten Widerstand mit R × U bezeichnet (wobei R die
Menge ist, welche man durch den Versuch erhalten soll), und den von den Unebenheiten
herruͤhrenden Widerstand gleich R × U² sezt, die Summe des Widerstandes R (U + U)² ist.
Prony, welcher alle seine große Fertigkeit auf die
Loͤsung aller Faͤlle der vorhergehenden Auctoren verwendete,
berechnete aus einer Auswahl von mehr als 50 Versuchen folgende einfache Formel:
U = 26,70 √(DZ/λ); hier ist U die mittlere Geschwindigkeit des Durchschnittes der Roͤhre, D der Durchmesser der Roͤhre, Z die Hoͤhe des Wassers und λ die Laͤnge der Roͤhre. Hiernach
scheint es, daß die Geschwindigkeit direct in dem zusammengesezten
Verhaͤltnisse der Quadratwurzeln des Durchmessers der Roͤhre und der
Hoͤhe des Wassers, und sich umgekehrt wie die Quadratwurzeln der
Laͤnge der Roͤhre verhaͤlt; d.h. bei jeder gegebenen
Wasserhoͤhe und jedem Durchmesser der Roͤhre verhalt sich die
Geschwindigkeit umgekehrt wie die Quadratwurzel der Laͤnge der
Roͤhre.
Vergleicht man diese Resultate mit jenen Dubuat's,
Girard's und Anderer, so wird man finden, daß sie einander
saͤmmtlich sehr nahe kommen. Im Allgemeinen gilt, daß wenn man eine
Roͤhre in einem Winkel von beinahe 6 1/2 Graden oder 1/9 ihrer Laͤnge
neigt, die entleerte Fluͤssigkeit beinahe jener gleich seyn wird, welche
durch Ansazroͤhren entleert wird. Nach einigen Auctoren ist die Speisung,
welche erfordert wird, um die mittlere Geschwindigkeit des Wassers, welches aus geraden
Roͤhren ausfließt, auszudruͤken, gleich V²/479.
Dr. Young gibt sie zu V²/550 an: die Verminderung der entleerten Fluͤssigkeit
haͤngt von der Zusammenziehung des Wassers und der Reibung der Roͤhre
ab.
Die Veraͤnderung, welche durch Winkel und Kruͤmmungen in der Richtung
des Wasserstrahles hervorgebracht wird, vermindert die Geschwindigkeit auf eine
merkwuͤrdige Weise. Dubuat stellte mehrere
Versuche hieruͤber an, allein die von ihm vorgeschlagene Formel, nach welcher
V²S²/m
Widerstand, welcher durch eine Kruͤmmung erzeugt wird, angibt, hebt die
Schwierigkeit nicht. An dieser Formel ist V die
Geschwindigkeit, S der Linus des Einfalls- oder
Zuruͤkwerfungswinkels, und in eine sich gleich bleibende Groͤße,
welche Dubuat auf 2998,50 bestimmte.
Obschon sich vernuͤnftiger Weise annehmen laͤßt, daß der Widerstand mit
den Quadraten der Sinus der Einfallswinkel im Verhaͤltnisse siehe, so ist
doch die Theorie des Hrn. Dubuat von Grund aus irrig,
indem nicht alle Theilchen des Wasserstrahles unter demselben Winkel
zuruͤkgeworfen werden, und indem ein betraͤchtlicher Theil der
Geschwindigkeit durch den ersten Winkel oder durch die erste Kruͤmmung, auf
welche die Fluͤssigkeit in der Roͤhre stoͤßt, aufgehoben wird.
Dieser Einwurf ist um so richtiger, als die Theorie Dubuat's gegen mehr als die Haͤlfte der Versuche, die er
anfuͤhrt, verstoͤßt. Eben so irrig sind aber auch Dr. Young's Annahmen, nach welchen sich der Widerstand
wie die winkelige Bewegung und die Kraft des Radius, dessen Index 7/8
betraͤgt, verhaͤlt; aus den obigen Versuchen geht dieß naͤmlich
hinlaͤnglich hervor.
Schließlich scheint es mir offenbar, daß die Reibung auf eine unendlich
mannichfaltige Weise angewendet werden kann. Die Bestimmung des Widerstandes,
welchen Schiffe und schwimmende Koͤrper bei ihrer Bewegung durch
Fluͤssigkeiten erfahren; das Gesez der Aufhaltung oder des Widerstandes,
welchen Muͤsse erfahren; die Ursache der Hindernisse, welche die Wellen des
Oceans an den Abhaͤngen der Ufer treffen; das Gleichgewicht der Erde etc.
– Alles dieß sind Fragen, welche in der Haushaltung der Mutter Natur von der
hoͤchsten Wichtigkeit sind, und deren endliche Loͤsung jezt bloß durch
eine Aufhaͤufung von Thatsachen erzwekt werden kann.
––––––––––
Nachschrift. Seitdem diese Abhandlung der Royal Society vorgetragen worden, haben die HH. Poncelet und Lesbros von Ingenieurcorps zu Metz
der franzoͤsischen Akademie einen Auszug aus einer langen Reihe von Versuchen
uͤber die Wassermenge, welche sich durch rechtwinkelige Oeffnungen von großen
Dimensionen entleert, vorgelegt. Diese Versuche wurden auf Kosten der
franzoͤsischen Regierung gemacht, und daher wurde auch nichts gespart, um
dieselben so weit als moͤglich auszudehnen. Der vorzuͤglichste Zwek
derselben war, das genaue Maß des Coëfficienten der Zusammenziehung, und die
Formen des Wasserstrahles bei verschiedener Hoͤhe und verschiedenem
Flaͤcheninhalte auszumitteln. Die Resultate hievon sind:
Daß bei einer Oeffnung von 20 Quadrat-Centimeter unter Hoͤhen von 1
Meter 68 Centimeter der Coëfficient 0,600 war; daß der Coëfficient
aber, wenn die Hoͤhe auf das 4 oder 5fache der Oeffnung vermindert wurde, auf
0,605 stieg, und sich dann rasch wieder auf 0,593 verminderte, wenn die Hoͤhe
abnahm.
Daß bei kleineren Oeffnungen, z.B. bei Oeffnungen von 10 bis 5
Quadrat-Centimetern, dasselbe Gesez Statt fand, indem der Coefficient
fuͤr Oeffnungen von 10 Centimetern relativ 0,611, 0,618 und 0,611,
fuͤr Oeffnungen von 5 Centimetern 0,618, 0,631, 0,623 betrug, und bei noch
kleineren Oeffnungen fortwaͤhrend bis zu 0,698 stieg.
Daß der mittlere Coëfficient fuͤr Wasser, welches uͤber Wehren
laͤuft, 0,400 ist: ein Coëfficient, der nur sehr wenig von jenem Bidone's abweicht.
Ich sehe mithin keinen Grund, der mich veranlaßte von den bereits angegebenen
Coëfficienten abzugehen.
Tafeln