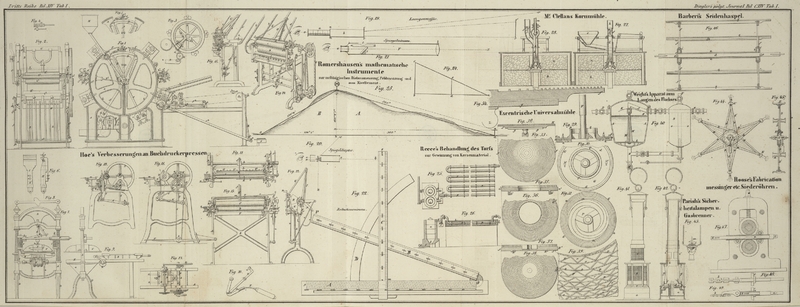
| Titel: | Romershausen's mathematische Instrumente zur militärischen Distanzmessung, zur Feldmessung und zum Nivellement. |
| Fundstelle: | Band 114, Jahrgang 1849, Nr. VII., S. 34 |
| Download: | XML |
VII.
Romershausen's mathematische Instrumente zur
militärischen Distanzmessung, zur Feldmessung und zum Nivellement.
Mit Abbildungen auf Tab.
I.
Romershausen's mathematische Instrumente zur Distanzmessung,
Feldmessung und zum Nivellement.
Dr. Romershausen zu Halle a.
S. hat neuerdings mehrere für Civil- und
Militärmessung hülfreiche Instrumente seiner Erfindung bekannt gemacht.
1) Der Längenmesser (Diastimeter) zur Messung von Linien und Distanzen aus einer Station.
Dieses Instrument mißt die diesen Distanzmessungen zum Grunde liegenden kleinen
Winkel nicht an dem Limbus eines Kreisbogens, sondern weit vortheilhafter durch das
Verhältniß eines veränderlichen Radius zu einer
constanten Tangente und gibt ohne weitere Rechnung die
entsprechende trigonometrische Linie. Bei der mit der Kleinheit der Winkel
wachsenden Vergrößerung des Radius gibt es das Maaß derselben mit einer Schärfe und
Genauigkeit in Secundentheilen, welche auf gewöhnlichem Wege mit den kostbarsten
Instrumenten nicht erlangt werden kann. Seine Messungen bieten daher bei gehöriger
Schärfe der Beobachtung mehr Sicherheit als die unmittelbare Kettenmessung,
vorzüglich bei coupirtem Terrain.
Der Längenmesser
Fig. 19
gleicht einem kleinen Taschenfernrohr
b mit einem Auszug a,
welcher die Scale des veränderlichen Radius enthält und
dessen Ocular mit einem feinen Sehloch o versehen ist
– während das Objectiv
c, c die constante Tangente
vermittelst höchst feiner, ein scharfes Einvisiren gestattender Stahlspitzen bildet.
Das Instrument enthält fünf solche sich aneinander anschließende getheilte Radien
und entsprechende Tangenten.
Die Messungen des Längenmessers bestehen darin, daß man
eine in der Entfernung am entgegengesetzten Ende der zu messenden Linie liegende
bekannte oder auch unbekannte Größe zwischen die Stahltangente des Objectivs c, c genau einvisirt. Dieses geschieht dadurch daß man
den Auszug a (rad.)
auszieht, wodurch der Sehwinkel (parallactische Winkel)
des vorliegenden Gegenstandes bis zum genauen Einschneiden desselben verkleinert
wird. Wäre z.B. die unbekannte Länge der Linie os zu
messen, nachdem in s zwei Signalstäbe in der Entferung
einer Ruthe = ss' senkrecht auf os aufgestellt sind, so richtet man bei zusammengestecktem Instrument die
untere, die Grundlinie bildende Stahlspitze der Tangente auf
s; ragt nun die Visirlinie der obern Stahlspitze or etwa über s' hinaus, so
zieht man den Auszug a langsam aus, wobei sich ox bis zum Schnitt von s'
hinanneigt und das geschlossene Dreieck oss' bildet. Ist
dieses erfolgt, so zeigt die Scale des rad. a ohne
weitere Rechnung die Länge der Linie os in Ruthen,
Fußen, Zollen etc.
Bezeichnen wir demnach die Scalenzahl des rad. mit n, die zu messende
Entfernung mit e und die
zu beobachtende vorliegende Größe mit s, so ist:
e = n
× s und s = e/n.
In diesem Falle ist entweder s
oder e
bekannt; sind aber beide
unbekannt, so werden in derselben Linie zwei etwas entfernte Beobachtungen
gemacht und aus der dabei gefundenen Differenz der Scalenzahl
n wird die Länge der Linie wie auch die Größe des
beobachteten entfernten Gegenstandes gefunden. Ist nemlich
x die unbekannte Größe des entfernten Objects,
y die unbekannte Entfernung desselben vom Standort,
n die im ersten Standort
gefundene Scalenzahl,
n' die im zweiten nähern
Standort gefundene Scalenzahl und
h die Entfernung der beiden Standpunkte,
so ist:
x = h/(n – n')
und y = x × n
2) Das Militärfernrohr zur Distanzmessung der Artillerie
etc. ist ein gutes achromatisches im Ocular mit einem die Tangente bildenden Mikrometer versehenes Fernrohr. Dieselbe Theorie des Diastimeters liegt auch diesem Instrument zum
Grund, nur mit dem Unterschied, daß bei diesem der Radius
constant und die Tangente veränderlich ist. Ein jedes gute Taschenfernrohr
kann mit dieser Einrichtung, unbeschadet seiner sonstigen Leistungen, versehen
werden, und die Distanzmessung desselben ist eben so einfach als die des
Diastimeters. Jedes dieser Instrumente erhält eine für dasselbe berechnete
trigonometrische Grundzahl = G. Wenn alsdann M die beobachteten Mikrometertheile und H die
eingeschnittene Größe des entfernten Objects
bedeuten, so ist die Entfernung
E = G/M × H. u.s.w.
Beide Instrumente erfordern zwar einige Uebung in der ihnen
eigenthümlichen Visirmethode, lösen aber das schwierige Problem der Distanzmessung
aus einer Station unstreitig auf die einfachste und sicherste
Weise. Eine vollständige Beschreibung derselben nebst praktischer Anleitung geben
die Schriften:
Romershausen's Spiegeldiopter und Längenmesser, der hülfreichste und bequemste Meßapparat etc. Halle
1845.
Desselben Militärfernrohr zur
Distanzmessung und militärischen Aufnahme. Halle 1848.
Desselben Theorie des Diastimeters.
Berlin b. Mittler.
Helmuth, die Distanzmessung der Artillerie und das
militärische Croquiren mit Hülfe des Romershausen'schen Längenmessers. Halle 184S.
3) Das Spiegeldiopter in Form eines kleinen
Taschenfernrohrs, dessen innere Einrichtung Fig. 20 zeigt.
Das Ocular hat zwei Durchsichten o und p, und das Objectiv einen damit correspondirenden Visirfaden. Im Innern des
angeschwärzten Rohres sind zwei feststehende Metallspiegel
a und b angebracht, welche
die Visirlinien paeh und obeh halbiren und dieselben in der Mitte ihrer Fläche senkrecht
durchschneiden. Zu beiden Seiten dieser Spiegel ist das Rohr mit vierseitigen
Oeffnungen durchbrochen, damit ein von außen einfallender Strahl die Spiegelflächen
trifft und von da zu dem Auge des Beobachters nach o und
p reflectirt wird. Die Spiegel selbst haben nach
optischen Grundsätzen folgende unverrückbare Stellung erhalten:
Der Spiegel
a ist so gegen die Visirlinie peh geneigt, daß ein außerhalb von der Seite einfallender Strahl da nur dann dem in p
beobachtenden Auge sichtbar wird, wenn er mit der directen Visirlinie peh auf das genaueste einen rechten Winkel bildet. Also:
< pad = < dah = 90°.
Der Spiegel
b ist dagegen so gestellt, daß der Strahl cb nur alsdann zu dem Auge des Beobachters nach o reflectirt wird, wenn derselbe auf der Visirlinie obh im Durchschnitte des Spiegels einen Winkel von 45° bildet, also:
< hbc
=
45°,
mithin
< obc
=
135°.
Da das Spiegeldiopter in freier Hand ohne Stativ gebraucht
wird, so gewährt es dem Geometer bei der Flächenausnahme vielseitige Vortheile und
Erleichterungen.
a) Er stellt sich damit selbständig und ohne fremde
Hülfe zwischen zwei Punkten und auf ihrem Alignement auf, kann in jedem Punkte der
gegebenen Linie Senkrechte errichten, auf dieselbe von
jedem außerhalb derselben
gegebenen Punkte Perpendikel Herabfällen und Parallelen ziehen.
b) Es gibt ihm unmittelbar auf dem Felde über der Grundlinie des Dreiecks die
Höhe desselben, mithin auch den Flächeninhalt weit genauer, als wenn derselbe erst aus der Zeichnung
entnommen werden soll, indem es zugleich den Entwurf derselben wesentlich
erleichtert und sichert.
c) Es construirt auf dem Felde das in vielen Fällen
höchst hülfreiche rechtwinkelig gleichschenklige Dreieck,
wodurch es bei coupirtem Terrain die Messung unzugänglicher Linien, die Breite von
Flüssen etc., die Aufnahme des Dreiecks bei dem bloßen Durchschreiten seiner
Grundlinie und die Messung von Höhen und Höhenabschnitten gestattet.
Das Spiegeldiopter unterscheidet sich demnach durch seine
beiden constanten Winkel wesentlich von dem alten Adam'schen Winkelspiegel, welcher nicht die Hälfte
seiner Leistungen gewährt und dessen Visirmethode weit unbequemer ist.In dem neuerdings erschienenen, sonst schätzbaren Werke von Schneitler – die Instrumente und Werkzeuge
der höhern und niedern Meßkunst etc. Leipzig 1848 – sind vorstehende
Instrumente aus offenbarem Mangel an Bekanntschaft mit ihrer neuern
Einrichtung etc. sehr unvollkommen beschrieben, und namentlich ist das Spiegeldiopter S. 57 völlig unrichtig verzeichnet
und dargestellt worden.
Vergl. obige Schrift: Romershausen's
Spiegeldiopter und Längenmesser etc. Halle
1848.
4) Das Spiegelniveau
Fig. 21. F das Fernrohr. b das Objectiv. o ein die Oculare
enthaltender Auszug.
Im Innern des Rohres ist oberhalb die empfindliche Libelle
a, b mit ihren Rectificationsschrauben angebracht; sie
erhält Licht durch den Ausschnitt des Rohres bei c.
Unter der Libelle liegt im Focus des Oculars ein feiner
Metallspiegel
s, welcher das Sehfeld des Fernrohrs halbirt und das
Bild der Luftblase derselben in die Visirlinie ox
reflectirt. Diese Visirlinie wird durch eine auf der entgegengesetzten Seite des
Spiegels im Focalpunkt angebrachte höchst feine Stahlspitze fixirt. Diese zeigt nun dem in o
beobachtenden Auge auf das schärfste die Horizontale
ox, sobald als die Luftblase der Libelle im Spiegel
zwischen ihre Rectificationszeichen tritt.
Da das Auge die genaue Einspielung der Libelle und den Schnitt der Horizontalen gleichzeitig bemerkt und die Luftblase sich zugleich scheinbar auf der entfernten Nivellirlatte darstellt, deren Maaß daselbst unmittelbar
abgelesen wird, so gewährt dieses Spiegelniveau die größtmögliche Sicherheit und
Bequemlichkeit, um so mehr, da die Libelle im Innern des
Rohres aufs vollkommenste geschützt ist.
Das Spiegelniveau mit Fernrohr ist vorzüglich für
Eisenbahnwege und Wasserbauten etc. bestimmt; für Bauhandwerker und nahe Erdarbeiten
wird dasselbe auch ohne Fernrohr angefertigt.
Vergl. Romershausen's Spiegelniveau,
ein neues und vollkommen sicheres Instrument zum Wasserwägen. Leipzig 1842.
Desselben Meßkunst für Landleute, Gärtner und Bauhandwerker
etc. Halle 1848.
5) Das Reductionsniveau
Fig. 22,
welches bei unebenem Terrain die gemessenen Linien unmittelbar auf dem Felde, ohne
weitere Rechnung auf den Horizont reducirt und ein sehr
vortheilhaftes Nivellement bei festen Zielpunkten
ausführt. A ein starkes Messinglineal, welches auf der Rückseite eine gute
Röhrenlibelle trägt. Auf der uns zugekehrten Fläche ist dasselbe von o bis g in 1000 gleiche
Theile und zwar mittelst Transversalen getheilt. Bei o
ist es mit einem starken Zirkelgewinde versehen, welches das zweite Lineal
B mit demselben verbindet.
Dieses Lineal
B hat von o aus eine völlig
gleiche Theilung wie A, so daß wenn es auf letzteres
niedergelegt wird, sämmtliche Theilstriche genau ineinander greifen. Es trägt auf
der Rückseite bei o ein Ocular und bei p ein Objectiv-Diopter, oder bei den bessern Instrumenten für größere
Sehweiten ein Fernrohr mit Fadenkreuz.
Das dritte Lineal
C steht auf A vollkommen
senkrecht und kann vermittelst einer Nuth in dieser Richtung auf A von o bis g leicht und sicher bewegt werden. Dieses senkrechte Lineal hat von m
bis s eine völlig gleiche Theilung wie A und B, und trägt bei n einen Nonius, welcher auf
den Transversalen von A die kleinern Maaßtheile, Fuße,
Zolle etc. angibt.
D ist endlich ein auf A
feststehender und aus dem Mittelpunkt o beschriebener
Sextant, dessen auf der Rückseite befindliche
Gradtheilung von einem an B befindlichen Nonius tangirt
wird und eine genaue Winkelmessung gestattet.
Die Bewegungen geschehen durch Zahn und Trieb und das Ganze wird unterhalb A vermittelst einer auf jedem einfachen Stativ
anzubringenden Vorrichtung mit Horizontal- und mikrometischer
Verticalbewegung getragen. Beides ist als an sich verständlich in der Zeichnung hinweggelassen.
Die Vortheile welche das Reductionsniveau zunächst
gewährt, beruhen in folgendem: Der natürliche Werth eines Grundstücks kann nur nach
dem Raum beurtheilt werden, den dasselbe als Horizontalfläche einnimmt, indem alle Gewächse nach verticalen, auf der
Horizontalfläche senkrechten Richtungen wachsen und also auf einer bergigen Flur
nicht mehr Früchte gewonnen werden, als auf ebenem Boden. Der ökonomische Grundriß einer Feldstur darf daher die verschiedenen
Erhöhungen und Vertiefungen des Terrains in ihren linearen Verhältnissen nicht
aufnehmen, sondern muß nur den Flächenraum entwerfen,
welchen die Grundstücke auf der Horizontalebene
einnehmen. Der gewissenhafte Feldmesser ist daher
genöthigt, jede von dem Horizont abweichende Linie vor der Aufnahme in die Zeichnung
auf den Horizont zu reduciren. Dieses war aber seither unstreitig nicht allein eine
der schwierigsten und mühevollsten Arbeiten, sondern auch der Grund öfterer
Unrichtigkeiten bei ökonomischen Vermessungen. Ein auffälliges Beispiel der
Nothwendigkeit dieser Reduction und der Vortheile, welche
das Reductionsniveau dabei gewährt, zeigt uns die Fig. 23. Bei
der Aufnahme der Bergfläche
AB hat der Feldmesser die
Linie ac und cd =
320° + 189°4' = 509°4' gemessen; wollte er diese locale
Ausdehnung in den Entwurf seiner Karte aufnehmen, so würde er nicht allein die
größte Verwirrung in dieselbe bringen, sondern auch den Besitzer hinsichtlich des
wahren nutzbaren Flächenraums bedeutend beeinträchtigen; denn die Linien der
horizontalen Ausdehnung ab und bd = 300° + 154°1' zeigen eine Differenz von 55°3'.
Er ist daher genöthigt diese Reduction auf den Horizont vorzunehmen. Dieses geschah
nun seither entweder oberflächlich dadurch, daß man bei der Kettenmessung der Linie
ac die verschiedenen Kettenzüge so gut als möglich
auf mechanische Weise in den Horizont einzurichten suchte, oder daß man die
gemessene Linie ac als die Hypotenuse und ab und bc als die Katheten eines rechtwinkeligen Dreiecks
abc betrachtete und nach Messung des Elevationswinkels
a die Länge der Horizontalen
ab durch trigonometrische Rechnung oder durch besondere
Reductionstabellen ermittelte. Ersteres ist immer ungenau und fehlerhaft, und
letzteres erfordert einen kostbarern Winkelmesser mit Niveau und ist mühsam und
zeitraubend.
Alle diese Uebelstände beseitigt das Reductionsniveau. Es
reducirt unmittelbar auf dem Felde jede gemessene Linie ohne weitere Rechnung
und Construction auf den Horizont
und gibt zugleich die senkrechte Höhe und den Elevationswinkel. Es gründet
seine Messung auf die Aehnlichkeit der Dreiecke abc und
ade
Fig. 24. Da
in diesen rechtwinkeligen Dreiecken de ∥ bc, so ist:
ad : de
=
ab : bc
ae : ad
=
ac : ab
ae : ed
=
ac : bc
u.s.w.
Wenn also in einem dieser Dreiecke die wirkliche, in der Natur gemessene Größe einer Seite bekannt ist, so läßt sich die der andern durch Rechnung
finden. Diese Rechnung ist aber bei dem Reductionsniveau
nicht erforderlich, da sämmtliche Seiten des von ihm gebildeten Dreiecks
ade gleiche Theilung haben, also ihr gegenseitiges
Verhältniß unmittelbar durch ihre Maaßstäbe anzeigen.
Wird demnach das Lineal
A des Instruments Fig. 22 im Standpunkt
a
Fig. 24
vermittelst der Libelle in die Horizontale
ab und das Lineal
B auf den Punkt c gerichtet,
so bildet es mit dem Lineal
C = de das kleine Dreieck
ade, welches nach obigem dem großen Dreiecke
abc vollkommen ähnlich ist. Ist nun in dem großen
Dreieck abc die wirkliche Größe
einer Seite, z.B. ac gemessen und wird das Lineal
B auf dem Punkt c und das
Lineal
C auf demselben Theilpunkt
des Maaßstabs von
B eingestellt, welcher der in der Natur gemessenen Länge
von ac entspricht, so gibt der Maaßstab auf
A die wirkliche horizontale
Länge von ab, und der Maaßstab auf
C die senkrechte Höhe von bc unmittelbar an, während der Sextant D beiläufig noch den Elevationswinkel a anzeigt.
Aus dieser Erörterung ist der praktische Gebrauch des Reductionsniveau an sich einleuchtend; wir wollen denselben beispielsweise
noch an Fig.
23 erläutern.
Zu diesen Messungen ist die hier auf dem Gipfel des Berges aufgestellte Zielscheibe
cm von bekannter und feststehender Höhe erforderlich.
m eine hölzerne mit Blech überzogene und wie die
Fig. zeigt, schwarz und weiß lackirte Scheibe. Am Fußende
ist dieselbe mit einem Stahlschuh und einer Eisenscheibe
c versehen, damit der Stab derselben stets in gleicher
Höhe in den Boden eingesetzt wird.
Der senkrechte Durchschnitt des Berges zerfällt in die beiden rechtwinkeligen Dreiecke
A und B. Wir erörtern hier
die Operation zunächst an dem Dreieck
A, indem ganz dasselbe Verfahren bei dem Dreieck B stattfindet. Die mit der Kette gemessene Hypotenuse
ac = 320° ist auf den Horizont zu
reduciren.
Wir stellen am Fuß des Berges in a das Reductionsniveau
n in gleicher Höhe mit der Zielscheibe cm über dem Boden auf; es ist demnach:
ac
∥
nm
und
ac
=
nm = 320°.
Jetzt richten wir das Lineal
A (Fig. 22) vermittelst der
Libelle genau in die Horizontale
nx = ab; visiren sodann das
Lineal
B vermittelst des Fernrohrs
auf den Mittelpunkt der Zielscheibe
m ein und rücken das senkrechte
Lineal
C genau auf den Theilstrich 320° der Hypotenuse
B.
Da nach dieser Operation die Hypotenuse des kleinen, von
dem Instrument gebildeten Dreiecks, das wirkliche in der
Natur gefundene Maaß der Hypotenuse
ac in die Verhältnisse des kleinen Dreiecks überträgt
und die Winkel dieselben sind, so zeigen nun die Maaßstäbe des Instruments das wirkliche Maaß
der beiden Katheten des großen Dreiecks
nx und mix. Also:
nm
=
320° = ac
nx
=
300° = ab
und
mx
=
109°4'5'' = cb.
Auf diese Weise erhalten wir also ohne weitere Rechnung etc.
unmittelbar auf dem Felde das Maaß der auf den Horizont reducirten Linie
ac und auch die senkrechte
Höhe des Berges bc mit großer Sicherheit und
Genauigkeit.
Da bei diesen Messungen die Zielscheibe und das Stativ des Instruments stets gleiche
Höhe haben, so ist auf die Höhe des letzteren über dem Horizont keine weitere
Rücksicht zu nehmen.
In dem Fall, daß der Bergabhang
Fig. 23
unzugänglich ist und die Linie ac nicht unmittelbar mit der Kette gemessen werden kann, erhalten wir
dieselben Resultate durch folgende Operation:
Wir messen am Fuß des Berges in dem Alignement ab eine
kleine Standlinie
ap = S, stellen das
Instrument in a auf, richten das Lineal
A vermittelst der Libelle
genau in den Horizont – das Lineal
B auf den Gipfel des Berges
c – und das Lineal
C auf das Maaß der Standlinie
S im Maaßstab von
A. Jetzt zeigt uns C das
Maaß der entsprechenden Höhenkathete = H.
Dasselbe Verfahren wiederholen wir in dem in gleichem Niveau liegenden zweiten Standpunkt
p und finden hier eine zweite
Höhenkathete = h. Nun ist:
ab = S
× h/(H – h)
und cb = H × h/(H
– h).
Richten wir endlich die Lineale des Instruments auf diese gefundenen Dimensionen im
Standpunkt
a, so zeigt uns C auch die
unbekannte Länge der Hypotenuse
ac.
Noch vortheilhafter ist es, wenn das Fernrohr des Lineals
B mit dem Mikrometer des
obigen Militärfernrohrs zur Distanzmessung versehen ist.
Lassen wir alsdann auf dem Gipfel des Berges in C ein
Signal von bekannter Größe
aufstellen, so finden wir durch eine einzige Beobachtung
im Standpunkt a
sämmtliche Dimensionen.
Aus dieser Darstellung ist es an sich einleuchtend, welche wesentlichen Vortheile das
Reductionsniveau auch dem Nivellement gewährt. Bei der gewöhnlichen Nivellirmethode stellt man das
Instrument in der Mitte zwischen den einzelnen Stationen auf und schreitet so mit
stets waagrechten Linien fort, um das Gesammtgefälle durch Addition und Subtraction
der verschiedenen Höhenverhältnisse zu finden. Es ist aber durch die Erfahrung
bestätigt, daß bei diesen vielfach zerstückelten Messungen und den wiederholten und
zeitraubenden Aufstellungen und Einrichtungen einer beweglichen Zielscheibe sich
mehr Fehler einschleichen, als wenn wir bei einem in bestimmter Höhe feststehenden Zielpunkte und durch Messung einer einzigen
der ansteigenden Bodenfläche parallel laufenden Ziellinie, das Gesammtgefälle durch eine
sorgfältige Beobachtung unmittelbar am Instrument
ablesen.
Diese letztere, bequemere und zuverlässigere Nivellirmethode gewährt nun das Reductionsniveau auf das vollkommenste. Vergl. Fig. 22, wo
eine einzige Beobachtung das Gefälle ca = cb = 109°5'' angab.
Eine vollständigere Beschreibung und Anleitung gibt die Schrift:
Romershausen's Reductionsniveau etc. Halle bei Heynemann
1848.
Tafeln