| Titel: | Bemerkungen zu Bunsen's Photometer; von C. Bohn. |
| Fundstelle: | Band 154, Jahrgang 1859, Nr. VI., S. 15 |
| Download: | XML |
VI.
Bemerkungen zu Bunsen's Photometer; von C. Bohn.
Aus den Annalen der Chemie und Pharmacie, Bd. CXI S.
335.
Mit einer Abbildung auf Tab. I.
Bohn, Bemerkungen zu Bunsen's Photometer.
Der sinnreiche Gedanke, welcher dem Photometer von Bunsen
zu Grunde liegt, und die größere Genauigkeit, welche mit diesem Meßinstrument
erreicht werden kann, haben dem neuen Photometer rasch den Weg gebahnt. Der
Erfinder, dem die Wissenschaft und die Technik der Apparate schon so viele
Bereicherungen verdanken, hat sich begnügt, die Idee anzugeben und deren
Brauchbarkeit darzuthun, – eine eingehende Besprechung des Instrumentes hat
er nicht veröffentlicht, – es ist von seinem Laboratorium aus bekannt
geworden.
Bekanntlich gründet sich das neue Photometer auf die Thatsache, daß befettetes Papier
das Licht in beträchtlich größeren Mengen hindurchläßt, als nicht befettetes, und
daß umgekehrt das Licht an befetteten Stellen in beträchtlich geringerer Menge
reflectirt wird, als vom reinen Papier. Ein Papierschirm mit einem Stearinfleck
erscheint daher im durchgelassenen Lichte an der befetteten Stelle Heller als an den
übrigen, während bei directer Beleuchtung die reinen Stellen Heller erscheinen.
Würde alles Licht, welches auf den Schirm fällt, nur in zwei Theile zerlegt –
einen Theil der reflectirt, und einen der durchgelassen wird – so würde, bei
gleich starker Beleuchtung der entgegengesetzten Seiten des Schirmes, dieser seiner
ganzen Ausdehnung nach nothwendig von derselben Helligkeit erscheinen, – der
Stearinfleck würde verschwinden. Denn bezeichnet α einen Bruch, der ausdrückt, welch ein Antheil des auffallenden
Lichtes von reinem Papier
reflectirt wird, und β einen Bruch der angibt,
welch einen Antheil des auffallenden Lichtes das Papier hindurchläßt, so ist, nach
der gemachten Voraussetzung der Zerlegung des Lichtes in nur zwei Theile, immer α + β = 1.
Bezeichnet J die Intensität des Lichtes, mit welchem
jeder Punkt der einen Seite des Schirmes direct beleuchtet wird, so drückt αJ die Intensität des zurückgeworfenen und βJ des durchgelassenen Lichtes aus. Wird die
andere Seite des Schirmes mit gleich intensivem Lichte beleuchtet, so wird auch dort
(angenommen das Papier sey auf beiden Seiten gleich) an allen Punkten Licht von der
Intensität αJ zurückgeworfen und Licht von der
Intensität βJ durchgelassen. Jeder Punkt des
Schirmes wird also gleichzeitig im reflectirten und im durchgelassenen Lichte
gesehen und erscheint in der totalen Helligkeit αJ + βJ = (α + β) J = J.
An den benachbarten, mit Stearin getränkten Stellen des Papieres ist dieß nicht
anders als an dem reinen Papier, denn wenn auch die Reflexions- und
Durchlassungscoefficienten α' und β' für befettetes Papier andere Werthe besitzen
als für reines, so ist doch immer, nach der gemachten Annahme, α' + β' = 1
und die Helligkeit eines jeden Punktes der befetteten Stelle ist α'J + β'J =
(α' + β')J = J,
d.h. gerade so groß wie die eines Punktes des reinen Papiers. Ist die aufgestellte
Hypothese richtig, so kann der Stearinfleck nicht mehr von dem reinen Papier
unterschieden werden, er muß verschwinden, sobald der Schirm auf beiden Seiten von
gleich hellem Licht getroffen wird.
So naheliegend die gemachte Annahme ist, so ist sie doch nicht zulässig, sie wird
durch den Versuch widerlegt. Die Beobachtung zeigt, daß der Fleck nicht
verschwindet, wenn der Schirm genau in die Mitte zwischen zwei Lichtquellen gleicher
Intensität gebracht wird. – Dieß deutet sofort an, daß das Licht nicht in nur
zwei Theile zerlegt wird; – es zerlegt sich in drei und der dritte Antheil wird absorbirt. Diese Annahme hat nichts
Befremdendes, da bekanntlich selbst die durchsichtigsten Körper Licht
absorbiren.
Es sollen die Brüche α, β, γ
ausdrücken, welche Antheile des auffallenden Lichtes vom reinen Papier
zurückgeworfen, durchgelassen und absorbirt werden. Dann ist immer:
α + β + γ = 1.
Für die befetteten Stellen des Papiers haben die Coefficienten der Zurückwerfung,
Durchlassung und Absorption des Lichtes andere Werthe; – sie seyen α', β', γ'. Immer aber ist:
α' + β' + γ' = 1.
Wird jeder Punkt der einen, z.B. der rechten Seite des Schirmes, von Licht, dessen
Intensität J ist, getroffen, so geht von jedem Punkte
der rechten Seite der reinen Papierfläche Licht von der Intensität αJ zurück und von jedem rechts gelegenen Punkte
der befetteten Stelle Licht von der Intensität α'J. Fällt auf der linken Seite des Schirmes überall Licht von der
Intensität J' auf, so kommt zu dem Lichte, welches von
den Punkten der rechten Seite ausgeht, noch durchgelassenes Licht, und zwar von der
Helligkeit βJ' für die Punkte der reinen, und von
der Helligkeit β'J' für die Punkte der befetteten
Stellen. Es erscheinen sonach die ersteren in der Totalhelligkeit αJ + βJ' und
die letzteren in der Helligkeit α'J + β'J'. Soll die Erkennbarkeit des Stearinflecks
verschwinden, so muß die Helligkeit eines Punktes desselben gleich seyn der
Helligkeit eines Punktes des reinen Papiers, – oder es muß seyn:
αJ + βJ' = α'J + β'J'.
Woraus folgt
J (α –
α') = J' (β' – β)
und unter Berücksichtigung der Gleichungen:
α + β + γ = α' + β' + γ' =
1
Textabbildung Bd. 154, S. 17
Man sieht, daß wenn für den Fall des Verschwindens des Flecks die Lichtintensität auf
beiden Seiten des Schirmes gleich wäre, d.h. J = J', alsdann auch γ =
γ' oder der Absorptionscoefficient des
reinen, gleich jenem des befetteten Papiers seyn müßte. Der Versuch zeigt, daß der
Stearinfleck nicht verschwindet für J = J', er zeigt ferner, daß derselbe auf der rechten Seite
(jener, die in jedem Punkte direct Licht von der Intensität J empfängt) nur dann verschwindet, wenn J' >
J. (Bei der im Versuche angewendeten Papiersorte und
Befettung mit Stearin ergab sich J' etwa zu 12/9 J.) Da nun die befettete Stelle, wie der erste Anblick
lehrt, weniger Licht reflectirt als die reinen Stellen, mit anderen Worten α' < α ist, so ist der Nenner des
Bruches in der vorstehenden Gleichung positiv. Da der Ausdruck in der Klammer größer
als 1 seyn muß, so muß auch der Zähler jenes Bruches positiv seyn, oder γ' < γ,
d.h. an der befetteten Stelle ist die Lichtabsorption geringer als an den reinen
Stellen.
Aus dem Vorangegangenen kann gefolgert werden:
daß der Stearinfleck niemals auf beiden Seiten des Papiers zu
gleich verschwinden kann.
Denn das Verschwinden des Flecks auf der rechten Seite verlangt, daß die linke
stärker beleuchtet sey als die rechte, während das Verschwinden des Flecks auf der
linken Seite nur dann eintreten kann, wenn im Gegentheil die rechte Seite intensiver
beleuchtet ist als die linke.
Aus α + β + γ = α' + β' + γ' und
α' < α, γ' < γ folgt noch unmittelbar β' > β.
Die angestellten Betrachtungen setzen stillschweigend voraus, daß die Bestrahlung
durch paralleles und senkrecht zur Schirmfläche auffallendes Licht erfolge, daß das
Auge des Beobachters eben so senkrecht der Schirmfläche gegenüber stehe, daß endlich
das Papier auf beiden Seiten gleiches Reflexionsvermögen besitze. Genau sind diese
Bedingungen im Versuche nicht zu erfüllen. Im Uebrigen ist leicht einzusehen, wie
bei einer Messung zu verfahren wäre. In einem dunkeln Zimmer müßte man den Schirm
auf der einen Seite durch irgend ein constantes Licht, das in constanter Entfernung
vom Schirme bleibt, beleuchten und müßte von der anderen Seite die zu vergleichenden
Lichtquellen, eine nach der anderen, in jene Entfernungen bringen, für welche der
Stearinfleck in der Mitte des Schirmes nicht mehr zu unterscheiden ist. Die
leuchtenden Körper und das Auge sind dabei senkrecht der Mitte des Schirmes
gegenüber zu stellen. Zweckmäßig wird es seyn, durch eine Röhre oder durch die hohle
Hand zu sehen, um das directe Licht abzuhalten. Die Quadrate der Entfernungen der
Lichtquellen von dem Schirme würden bekanntlich das Verhältniß der Lichtstärken
angeben.
Weit bequemer und exacter wird die photometrische Messung, wenn man passend geordnete
Spiegel mit dem Papierschirm verbindet und die Beobachtung an den Spiegelbildern
ausführt.Solche Spiegel-Photometer sind längst im Gebrauch, ohne daß bekannt
ist, durch wen diese Abänderung des Bunsen'schen
Photometers eingeführt wurde. Die Spiegel sind unter einem Winkel von
ungefähr 120° verbunden. Die Bildflächen fallen hiernach nicht in
eine Ebene, wie bei rechtwinkelig gegen einander stehenden Spiegeln. Die
kleine Modification, die Spiegel unter rechtem Winkel zu verbinden, gewährt
mehrere namhafte Vortheile. Es hat keine Schwierigkeit, das Auge in eine
Richtung zu bringen, welche genau senkrecht zu einer beliebigen Stelle der
Bildfläche ist, und die zu vergleichenden Lichter können leicht so
aufgestellt werden, daß das Licht tangirend zu den Spiegeln wird, keiner
derselben direct von Licht getroffen wird. Wer diese alteren
Spiegel-Photometer geprüft hat, weiß, daß mit denselben keine
brauchbaren Resultate zu erzielen sind. Es wird sich aber zeigen, daß unter
Anwendung rechtwinkelig verbundener Spiegel und unter Berücksichtigung
einiger, im Texte bezeichneter Punkte eine Schärfe der Messung erreicht
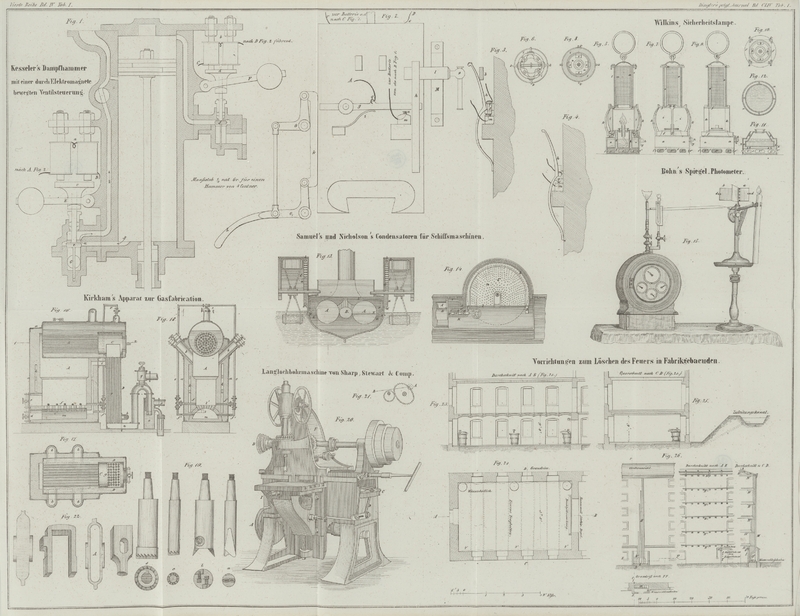
werden kann, die 2 Procent der zu messenden Größe sicher erkennen läßt. Die nach einer Photographie des benutzten Apparates verfertigte Abbildung in
Fig. 15
wird mit einem Blicke die Einrichtung erläutern. Zwischen zwei rechtwinkelig verbundenen Spiegeln a und b ist der Papierschirm
an einem Metallrähmchen unter 45° gegen jeden der Spiegel befestigt; –
die beiden Bilder desselben liegen also in einer Ebene.
In der verlängerten Richtung des Spiegels a, in
beliebiger, aber unveränderlicher Entfernung (30 Centimeter) ist ein möglichst
constantes Licht (Wachs- oder Stearin-Kerze, – die den
Verträgen mit Gasfabriken zu Grunde liegende Normalkerze) befestigt und in der Ebene
des linken Spiegels b, in gleicher Höhe mit der Flamme
des Normallichtes, ist am Ende eines um die Rolle c
geschlungenen Maaßbandes der auf seine Intensität zu prüfende leuchtende Körper
angebracht. Direct auf die Spiegel darf kein Licht fallen, sie sollen nur tangirt
werden. Dieß ist erreicht, wenn der Schatten der sehr wenig vorstehenden Haken d, d, welche die Spiegel in ihrer Lage festhalten, genau
auf die Durchschnittslinie der Spiegel fällt, wenn kein scharf begränzter hellerer
Lichtstreif von den Spiegeln reflectirt und eben so wenig ein Schatten der Spiegel
auf dem Schirme wahrgenommen wird. Der Papierschirm tritt hinlänglich vor, um ein
directes Bestrahlen jenes Spiegels unmöglich zu machen, der senkrecht auf die Linie
vom Lichte zur Durchschnittslinie der Spiegelebenen gerichtet ist. Der Stearinfleck
ist auf dem Schirme möglichst nahe an der Durchschnittslinie der Spiegelebenen
angebracht, seine zwei Bilder liegen deßhalb sehr nahe beisammen. Stellt sich der
Beobachter so, daß er genau auf die hohe Kante des Schirmes sieht, so läßt eine sehr
geringe Verrückung des Auges aus der angegebenen Stellung nach Links den links
gespiegelten und eine eben solche Verrückung des Auges nach Rechts den rechts
gespiegelten Fleck genau senkrecht gegen die gemeinschaftliche Bildebene erblicken.
Die Helligkeit der Bilder hängt, unter sonst gleichen Umständen, lediglich von der
Beschaffenheit der Spiegel ab. Hier leisten die mit Silber belegten Spiegel des Hrn.
v. Liebig, wie in allen Fällen der Anwendung von Spiegeln
zu optischen Instrumenten, vortreffliche Dienste, die sofort einleuchtend sind, wenn
man sich an die Messungen des Hrn. v. Steinheil
erinnertPolytechn. Journal Bd. CXLVIII S.
465., nach welchen die Liebig'schen Silberspiegel 92
Proc., die besten Quecksilberspiegel aber nur 56 Proc. des auffallenden Lichtes
zurückgeben. Es ist dieß besonders hervorzuheben, weil die Empfindlichkeit des
Apparates wesentlich unter Anwendung der Silberspiegel erhöht wird. – Die
beiden Spiegel sind aus einem Stücke geschnitten.
Es ist leicht einzusehen, daß bei gleicher Beleuchtung der beiden Seiten des Schirmes
der Fleck weder aus dem Bilde im einen, noch aus dem Bilde im anderen Spiegel
verschwinden kann. Es geht dieß aus Betrachtungen hervor, die den früher
angestellten für einen Schirm ohne Spiegel ähnlich sind. Nur ist der Fall insofern
zusammengesetzter, als das von dem Schirme nach den Spiegeln gelangende Licht dort
zurückgeworfen wird, den Schirm von Neuem beleuchtet und theils durch Reflexion an
dem Papier, theils durch Durchdringung desselben abermals zu den Spiegeln gelangt.
Es erfährt an diesen neue Reflexionen und macht unendlich oft auf verschiedene Arten
den Weg zwischen den zwei Spiegeln. Hierdurch wird eine Modification in der
Helligkeit des Schirmes hervorgebracht, – sie wird beträchtlich vermehrt.
Die leuchtenden Körper seyen in der oben näher angegebenen Weise aufgestellt; J bezeichne die Intensität jenes Lichtes, welches von
der rechtsstehenden Lichtquelle direct nach einem Punkte der rechten Seite des
Schirmes gelangt, J' die Intensität des Lichtes, welches
von dem linksstehenden leuchtenden Körper direct auf einen Punkt der linken Seite
des Papierschirmes fällt. Denkt man sich für einen Augenblick die Spiegel nicht
vorhanden, so wären, wie in dem vorigen Falle:
(Jα + J'β), (J'α + Jβ) und (Jα' +
J'β'), (J'α' + Jβ')
die Helligkeiten des Lichtes, das von den rechts und links
gelegenen Punkten der reinen Papierfläche und von den rechts und links gelegenen
Punkten der befetteten Stellen ausgeht.
Aber es werden durch die Anwesenheit der Spiegel diese Helligkeiten erhöht und den
erhöhten Helligkeiten ist die Intensität der Bilder proportional.
Die Vermehrung, welche die Intensität (Jα + J'β) erfährt, hängt offenbar nur von den
Coefficienten α und β und von dem Bruche m ab, der angibt,
welch ein Antheil des auffallenden Lichtes von den Silberspiegeln zurückgeworfen
wird, oder mit anderen Worten: diese Vermehrung ist eine Function der genannten
Größen. Sie werde durch f (α, β, m) bezeichnet, so ist die Intensität des Lichtes,
welches ein Punkt der rechten Seite des Papiers nach dem rechten Spiegel sendet:
(Jα + J'β) f (α, β, m) oder kürzer geschrieben (Jα + J'β) F.
Die Lichtintensität (J'α + Jβ) erfährt dieselbe Vermehrung, denn alle Verhältnisse sind
dieselben, sie wird also zu:
(J'α + Jβ) f (α,
β, m) = (J'α + Jβ) F.
Für die Helligkeiten (Jα' +
J'β') und (J'α' + Jβ') welche sich auf
Punkte der befetteten Stelle beziehen, ist es im Wesentlichen nicht anders. Nur der
absolute Werth ihrer Vermehrung ist ein anderer, da sie Function der Größen α', β', m ist, deren zwei erste andere
Werthe haben als bei dem
reinen Papier. Die allgemeine Form der Function ist dieselbe, da der Weg des Lichtes
derselbe wie vorher. Man kann also sogleich schreiben:
Intensität des Lichtes, welches ein rechts gelegener Punkt der befetteten Stelle nach
dem rechten Spiegel aussendet:
(Jα' + J'β') f (α', β', m) = (Jα' + J'β') F
und
Intensität des Lichtes, welches ein links gelegener Punkt der befetteten Stelle nach
dem linken Spiegel aussendet:
(Jα' + Jβ') f (α', β', m) = (J'α' + Jβ') F'.
Würde kein Licht absorbirt, so müßte die Helligkeit des gesammten, von zwei
gegenüberliegenden Punkten des Schirmes ausgehenden Lichtes gleich seyn der
Helligkeit des gesammten, diese Punkte treffenden Lichtes. Das Licht erleidet aber
auf seinem Wege Absorptionen und jede der Intensitäten:
(Jα + J'β) F + (J'α + Jβ) F
und
(Jα' + J'β') F' + (J'α' + Jβ') F'
muß daher kleiner seyn als J + J'.
Die eintretenden Verminderungen der Helligkeiten hängen ab: von den Intensitäten J und J', von dem
Absorptionscoefficienten γ, beziehungsweise γ', und von dem Bruche δ, der den von den Spiegeln absorbirten Antheil des auffallenden
Lichtes angeben soll; die Verminderungen sind, mit anderen Worten, Functionen der
genannten Größen, und zwar hat die Function in den beiden Fällen, da die allgemeinen
Verhältnisse dieselben sind, dieselbe allgemeine Form, die durch das Zeichen φ angedeutet werden möge.
Es können somit die Gleichungen:
(Jα + J'β) F + (J'α + Jβ) F = J + J'
– φ (J, J',
γ, δ)
und
(Jα' + J'β') F + (J'α' + Jβ') F' = J + J' – φ (J', J, γ', δ)
aufgestellt werden.
Es ist nicht nöthig, die Function φ zu entwickeln,
da auch ohnedieß einleuchtet, daß ihr Werth, das ist die Verminderung der
Lichtintensität, unter sonst gleichen Bedingungen für jenen Fall der größere ist,
für welchen der Absorptionscoefficient den größeren Werth hat. Wie gefunden ist γ > γ'; also
ist die Helligkeit des gesammten, von den gegenüberliegenden Punkten des reinen
Papiers ausgehenden Lichtes kleiner als die Helligkeit
des gesammten, von
den gegenüberliegenden Punkten der befetteten Stelle ausgehenden Lichtes. In Zeichen
ausgedrückt:
(A.) (Jα + J'β) F + (J'α + Jβ) F < (Jα' + J'β') F' + (J'α' + Jβ') F'.
Soll der Fleck im Spiegel verschwinden, so muß die Helligkeit seines Bildes gleich
seyn der Helligkeit des Bildes der benachbarten Punkte des reinen Papiers. Und da
die Helligkeit eines Spiegelbildes proportional ist der Intensität des Lichtes,
welches vom Gegenstande nach dem Spiegel gelangt, so erhält man folgende
Bedingungsgleichungen:
für das Verschwinden des Flecks im rechten Spiegel:
(Jα + J'β) F = (Jα' + J'β') F'
und für das Verschwinden des Flecks im linken Spiegel:
(J'α + Jβ) F = (J'α' + Jβ') F'.
Gleichzeitig können diese beiden Bedingungen nie erfüllt seyn, sonst würden in der
Ungleichheit (A.) die zwei Glieder links einzeln den
zwei Gliedern rechts gleich, was mit dem Bestehen der Ungleichheit unverträglich
ist:
Also „kann der Fleck nie gleichzeitig in beiden Spiegeln
verschwinden.“ Ferner:
„kann der Fleck nicht im Spiegel verschwinden, wenn die Beleuchtung des
Schirmes auf beiden Seiten gleich intensiv ist,“
weil alsdann die Bedingung des Verschwindens des Flecks für
beide Spiegel zugleich erfüllt wäre, was so eben als unmöglich erwiesen wurde.
Die gewonnenen Resultate stimmen mit denjenigen überein, welche sich für den
Papierschirm ohne Spiegel ergaben; – der Versuch bestätiget sie.
Für das Verschwinden des Flecks auf einer Seite des Bunsen'schen Photometers ohne Spiegel ist eine einfache Relation ermittelt
worden zwischen den Lichtintensitäten J und J', von welchen die beiden Seiten des Schirmes
beleuchtet werden, und den Coefficienten α, α',
γ, γ' der Reflexionsfähigkeit und des Absorptionsvermögens
des reinen und des mit Stearin getränkten Papiers. Für das Verschwinden des Flecks
in einem der Spiegel läßt sich gleichfalls eine solche Relation finden. Um sie
aufzustellen ist es aber nöthig, die Functionen f (α, β, m) und f
(α', β', m), welche die Vermehrung der
Helligkeit der Punkte des Schirmes durch die Wirkung der Spiegel angeben,
vollständig zu entwickeln. Die Entwickelung dieser Function bietet zwar keine
Schwierigkeiten – es handelt sich einfach um Summation geometrischer Reihen
–, allein sie ist nicht ohne Weitläufigkeit zu bewerkstelligen. Das Resultat
der Entwickelung ist eine ziemlich zusammengesetzte Formel, deren Nutzen nur ein
sehr geringer, denn um mit ihrer Hülfe das Verhältniß J : J' für den Fall des Verschwindens des Flecks abzuleiten,
wäre vor allem die Kenntniß der numerischen Werthe von α, β, γ, α', β', γ' und m nöthig. Die Bestimmung derselben ist selbst schon eine
ziemlich umständliche Arbeit und müßte für jedes einzelne der vorgeschlagenen
Meßinstrumente gemacht werden, da selbst unter Anwendung des gleichen Papiers α', β', γ' doch wesentlich von der
größeren oder geringeren Sättigung des Papiers mit Stearin abhängen wird. Es wird
also von der Aufstellung einer solchen Relation als Function der genannten
Coefficienten Umgang genommen und das Verhältniß J : J' aus Versuchen mit dem Apparate selbst abgeleitet. Zu
diesem Zwecke sind zwei gleich intensiv leuchtende Körper in solche Entfernungen zu
bringen, daß das Bild des Flecks in einem Spiegel verschwindet. Verkehrt wie die
Quadrate der Entfernungen, verhalten sich die Intensitäten J : J' für den einen Spiegel, und ähnlich kann
das Verhältniß dann auch für das Verschwinden des Flecks im anderen Spiegel gefunden
werden. Gleich intensive Lichtquellen sind aber sehr schwer zu finden; – ohne
vorgängige photometrische Untersuchung darf man keineswegs annehmen, ein Paar
Wachs- oder Stearinkerzen aus demselben Packet, von gleichem Gewichte und aus
derselben Fabrik stammend, leuchteten auch nur annähernd gleich hell. Später
mitzutheilende Versuche werden dieß bestätigen.
Ist durch irgend welche Versuche das Verhältniß J : J' einmal festgestellt, so liegt der Gedanke nahe, die
erworbene Kenntniß in Verbindung mit einigen anderen Versuchen zur Ermittelung der
numerischen Werthe von α, β, γ,
α', β', γ' zu benutzen. Wie bereits erwähnt sind aber
die Formeln, aus welchen man diese Größen ableiten müßte, allzu complicirt und
erscheinen zu numerischen Bestimmungen nicht brauchbar.
Die Lichtquelle, welche direct die rechte Seite des Papierschirmes beleuchtet, ist in
einer constanten Entfernung vom Stearinfleck. Diese Entfernung wird im Folgenden zur
Einheit genommen.
Der Versuch lehrt, daß man links in der Entfernung D ein
Licht von derselben Intensität, wie das rechts in der Entfernungs-Einheit
stehende, anbringen muß, um das Bild des Flecks im rechten Spiegel verschwinden zu machen. Es bezeichne Jz die Intensität
des Lichtes, das direct auf einen, dem Spiegel, in welchem der Fleck verschwindet,
zugewendeten Punkt des Schirmes fällt, und Ja die Intensität
jenes Lichtes, das direct auf einen demselben Spiegel abgewendeten Punkt des Schirmes fällt. Das Ergebniß des Versuches läßt
sich dann in der Proportion
Jz : Ja = 1 : 1/D²
aussprechen.
Ein zweiter Versuch lehrt, daß, um den Fleck im linken
Spiegel verschwinden zu machen, die Kerze links in der Entfernung Δ angebracht seyn muß, während die gleich
intensive Kerze rechts in der Entfernung 1 bleibt. Dieser zweite Versuch gibt die
Proportion:
iz : ia = 1/Δ² : 1,
in welcher iz und ia die Intensitäten des Lichtes bedeuten,
welches direct auf einen Punkt der dem linken Spiegel zugekehrten und der ihm abgewendeten Seite des
Schirmes fällt.
Das Verschwinden des Flecks in einem Spiegel hängt ab von dem Verhältniß der
Intensität der Erleuchtung auf der dem Spiegel zugekehrten Seite des Schirmes, zur
Intensität der Erleuchtung auf der dem Spiegel abgewendeten Seite, d. i. im ersten
Versuche von Jz :
Ja, im
zweiten Versuche von iz : ia.
Da die Spiegel sich unter ganz gleichen Bedingungen finden, so muß das
Intensitätsverhältniß auf der zu- und abgewendeten Seite des Schirmes, für
den Fall des Verschwindens des Flecks, für beide Spiegel dasselbe seyn, oder es
ist:
Jz : Ja = iz : ia
und mit Rücksicht auf die vorhergehenden Proportionen:
1 : 1/D² = 1/Δ² : 1,
woraus
D = 1/Δ oder DΔ = 1².
Die Messungen werden zeigen, ob dieses Verhältniß exact stattfindet. Aus der
Abweichung des Productes der gemessenen Längen von der Einheit, in welcher sie
ausgedrückt, wird ein Schluß auf die Gränzen der in beiden Messungen begangenen
Fehler gemacht werden können, wenn man die absolute Gleichheit der Intensität der
beiden Kerzen annimmt. – Der unvermeidliche Fehler in der Messung kann für
verschiedene Beobachter, die dasselbe Instrument benutzen, verschieden seyn,
– weniger wegen der ungleichen Uebung der Experimentatoren, als wegen der
ungleichen Empfindlichkeit ihrer Augen gegen Helligkeitsdifferenzen.
Sind die Größen D und Δ für einen Apparat einmal bestimmt, so ist es sehr leicht, dieses
Instrument so herzurichten, daß jeder Beobachter
hinlänglich genaue Messungen mit demselben ausführen kann.
Auf das Maaßband werden die Längen D, D√2, D√3, D√4, D√5... und die Längen Δ, Δ√2, Δ√3, Δ√4, Δ√5.... getragen; an die Endpunkte der
ersteren die Zahlen 1, 2, 3, 4, 5.... mit schwarzer Farbe gesetzt, und an die Endpunkte der
letzteren Längen dieselben Zahlen, aber mit rother Farbe. Der Nullpunkt der Theilung
liegt in der Spitze eines am Bande befestigten Hakens; diese Spitze ist beim
Gebrauche möglichst genau auf die Mitte des leuchtenden Körpers einzustellen.
Die zu prüfende Lichtquelle, oder wenn sie feststehend der Apparat selbst, mit der
brennenden Normalkerze in der constanten Stellung rechts, werden so lange
verschoben, bis die Lichtquelle genau in der Ebene des linken Spiegels steht und das
Bild des Flecks im rechten Spiegel verschwindet. Das Maaßband wird ausgezogen, bis
die Spitze des Hakens auf die Mitte des leuchtenden Körpers kommt, – die
Entfernung des leuchtenden Körpers von dem Stearinfleck ist gleich der Länge des
Maaßbandes, die zwischen der Spitze des Hakens und einem kleinen, die Rolle, um
welche das Band geschlungen, überbrückenden Zeiger enthalten ist. Möge
beispielshalber gerade die mit schwarzer Farbe geschriebene Zahl 5 unter dem Zeiger
stehen, dann ist die Distanz der Lichtquelle vom Stearinfleck D√5. Bezeichnet nun x die Intensität
der Lichtquelle für die Entfernungseinheit und bezeichnet N dieselbe Größe in Bezug auf das Normallicht rechts, so ist die
Intensität des auf die linke Seite des Schirmes direct auffallenden Lichtes oder Ja = x/(D√5)² es
ist Jz = N.
Da aber:
Jz : Ja = 1 : 1/D² = D² :
1,
so ist
x/5D² . D² = N oder x = 5N,
d.h. die Lichtquelle hat die fünffache Intensität des
Normallichtes.
So das Ergebniß des ersten Versuches. Man wird sogleich einen zweiten zur Controle
folgen lassen, indem man durch passende Verschiebung das Bild des Flecks im linken
Spiegel zum Verschwinden bringt. Auf der rothen Theilung
findet man alsdann die Zahl 5, d.h. die Entfernung der Lichtquelle beträgt Δ√5. Jetzt ist also Jz = x/(Δ√5)² und Ja = N.
Erinnert man sich an die Proportion Jz : Ja = 1/Δ² : 1, so erhält man x/5Δ² : N = 1/Δ² : 1, oder x
= 5N, wie vorher.
Ist der genaue Werth von x wirklich 5N, so wird, im Allgemeinen, bei keiner der beiden
Einstellungen der Zeiger gerade auf die Zahl 5 fallen, sondern etwas darüber oder
darunter. Da die Umstände beim Einstellen auf das Verschwinden des Flecks in beiden
Spiegeln so ziemlich die gleichen sind, so steht zu vermuthen, daß der eine Versuch
etwas mehr, der andere etwas weniger als 5 Lichtstärken angeben wird. Sind die
Unterschiede der auf der schwarzen und auf der rothen Theilung gefundenen Angaben
nur gering, so kann das arithmetische (genauer das geometrische) Mittel aus beiden
ohne merklichen Irrthum als Verhältniß der gesuchten Lichtintensitäten angesehen
werden. Sind die Unterschiede in den Angaben bedeutend, betragen sie schon eine
halbe Lichtstärke, so zeigt dieß an, daß man entweder recht schlecht beobachtet,
oder daß die Helligkeit der Lichter von einem Versuche zum andern sich geändert hat.
Alsdann sind die Versuche zu wiederholen.
Die angegebene Art der Theilung erlaubt nur ganze Lichtstärken mit Sicherheit zu
bestimmen, – will man auch die halben noch mit Genauigkeit finden können, so
darf man nur die Längen D√1/2, D√3/2, D√5,2,
D√7/2... und Δ√1/2, Δ√3/2, Δ√5/2, Δ√7/2...... auf das Maaßband tragen und die Zahlen 1/2, 1
1/2, 2 1/2, 3 1/2... dazu schreiben.
Für den technischen Gebrauch, der bei der Construction des Apparates besonders vor
Augen lag, nämlich für die Ueberwachung der Gasbeleuchtungen, reicht diese Theilung
vollkommen aus.
Will man größere Genauigkeit, – der Apparat gestattet sie zu erreichen. Nur
muß man dann auf die Bequemlichkeit verzichten, die Lichtstärken sogleich an dem
Maaßbande ablesen zu können und muß sich zu einer kleinen Rechnung verstehen.
D und Δ sind, als
durch Fundamentalversuche ermittelt, bekannt vorausgesetzt. – Die Längen, bis
zu welchen das Maaßband ausgezogen werden muß, werden in Centimeter und Millimeter,
oder Zollen und Linien gemessen. Seyen sie e und η für das Verschwinden des Flecks im rechten und
im linken Spiegel, so findet man aus dem ersten Versuche: x = e²/D² N = e²Δ² . N und aus dem zweiten x =
η²D² N = η²/Δ² . N.In diesen Gleichungen müssen natürlich D und Δ in derselben Einheit ausgedrückt seyn,
wie e und η.
Diese vier Werthe von x sind einander gleich, woraus mit
Leichtigkeit gefolgert werden kann: eΔ =
ηD oder e/η = D². Die
Betrachtung dieser
Ausdrücke lehrt: Daß zu dieser photometrischen Messung mit dem Apparate nicht einmal
die Kenntniß der für jedes Instrument individuellen Größen D und Δ erforderlich ist; man hat nur
nöthig, die Längen e und η zu messen, für welche das Bild des Flecks einmal im rechten, das
anderemal im linken Spiegel verschwindet; diese mit einander multiplicirt und durch
das Quadrat des Abstandes der Normalkerze vom Stearinfleck dividirt, geben eine
Zahl, welche das Verhältniß der Intensität der untersuchten Lichtquelle zur
Intensität der Normalkerze angibt. Bei dieser Art der Messung entbehrt man freilich
der Annehmlichkeit der Bestätigung durch einen sofort anstellbaren Gegenversuch.
Will man einen solchen machen, so muß man die Entfernung der Normalkerze vom
Stearinfleck ändern.
Der Ausdruck e/η = D² zeigt aber noch etwas Wichtigeres an, nämlich
daß es möglich ist, die Werthe D und Δ genau zu bestimmen, ohne daß man über
Lichtquellen von gleicher Intensität verfügen kann. Man macht mit einer beliebigen
Lichtquelle zwei Versuche; in dem einen bringt man den Fleck im rechten Spiegel zum
Verschwinden, im andern Versuche im linken Spiegel. Die Quadratwurzel aus dem
Quotienten der in beiden Versuchen gefundenen Entfernungen der Lichtquelle vom
Stearinfleck gibt den Werth von D. Diese Bestimmung läßt
sich mit Hülfe verschiedener Lichtquellen beliebig oft leicht wiederholen, –
der Werth von D kann sonach mit großer Genauigkeit
gefunden werden.
Es sollen nun noch einige Versuche mit dem Spiegelphotometer angegeben werden. Sie
werden ohne weiteres die Fehlergränzen, wie sie sich für den Verfasser stellen,
erkennen lassen. – Es sey noch bemerkt, daß die hier mitgetheilten Versuche
die ersten sind, welche überhaupt angestellt wurden, es war also bei ihrer Vornahme
keinesweges eine besondere Uebung bereits erworben.
I. Vergleichung zweier Wachskerzen A und B, die beide als
„Normalkerzen, wie sie dem Vertrage des Münchener Magistrates mit
der dortigen Gasfabrik zu Grunde liegen“ bezeichnet
sind.
War die Kerze A rechts in der constanten Entfernung von
30 Centimeter gehalten, so mußte die Kerze B links in
die Entfernungen e = 21c, 9 und η = 26c,5 gebracht werden, um den Stearinfleck im
rechten und dann im linken Spiegel verschwinden zu machen. Es berechnet sich
hieraus:
Textabbildung Bd. 154, S. 27
War die Kerze B rechts in der constanten Entfernung von
30c gehalten, so mußte die Kerze A links in die Entfernungen 33c,7 und 41c,0
gebracht werden, um den Fleck im rechten und dann im linken Spiegel verschwinden zu
machen. Es berechnet sich hieraus:
Textabbildung Bd. 154, S. 28
Die beiden Versuche bestätigen einander. Denn die daraus abgeleiteten Werthe von D sind fast identisch, – das Verhältniß der
Intensität der Kerze A zur Intensität der Kerze B ist gefunden: 1 : 0,645 und das Umgekehrte ergibt der
Versuch 1 : 1,538, während die Rechnung 1 : 1/0,645 oder 1 : 1,550 angibt.
Es zeigen diese zwei Messungen ferner, in welch' bedeutenden Irrthum man verfallen
wäre, hätte man die Kerzen, weil sie aus einem Packet derselben Fabrik stammen, als
gleich hellleuchtend ansehen und unter dieser Annahme die Fundamentalverhältnisse
D und Δ bestimmen
wollen. – Zugleich lehren sie aber auch, wie unsicher es ist, bei Verträgen
über Erleuchtung Kerzenlicht als Einheit der Lichtintensitäten zu unterlegen. Zwei
gleich sorgfältig ausgeführte Messungen, deren eine auf die Normalkerze A basirte, die andere aber auf die Normalkerze B, hätten am 5. Juli die Intensität einer gewissen
Gasflamme in München zu 14 oder 21 1/2 Kerzenhelle angegeben.
Untersuchungen mit mehreren Stearin- und Wachskerzen, die je paarweise aus
demselben Packet genommen waren und vor Beginn der Untersuchung hinlängliche Zeit am
selben Orte gebrannt hatten, zeigten überall merkliche Ungleichheiten der
Intensitäten. Die Stearinkerzen waren im allgemeinen weniger verschieden als die
Wachskerzen, und zufällig waren die zwei „Normalkerzen“ jene,
welche hinsichtlich der Intensität ihres Lichtes die größte Verschiedenheit
zeigten.
Photometrische Messungen, mit Kerzen angestellt, werden immer leicht an einiger
Unsicherheit leiden, die nur durch große Behutsamkeit zu vermeiden ist. Der
geringste Luftzug verändert die Intensität der Kerzenflamme und ihre Stellung;
werden die Messungen zur Controle vertragsmäßiger Verpflichtungen angestellt, so
muß, außer dem Vorhergehenden, auch noch an den Umstand erinnert werden, daß die
Helligkeit, mit welcher ein und dieselbe Kerze leuchtet, auch von der Temperatur des
Raumes, in welchem sie brennt, abhängig ist. Die angedeuteten Gründe lassen es daher
gerathen erscheinen, bei Verträgen mit Gasfabriken nicht Kerzenflammen, und
besonders nicht Wachskerzenflammen, als Lichteinheit zu Grunde zu legen.
II. Vergleichung der Helligkeit einer
Lampe mit doppeltem Luftzuge mit jener der Normalkerze
A.
Verschwinden des Flecks im
Distanz der
rechten Spiegel
linken Spiegel
Kerze
Distanz der Lampe
30c
e = 57c
η = 69c,5.
Die äußersten Gränzen, zwischen welchen man, ohne einen deutlich hervortretenden
Fleck im Spiegel wahrzunehmen, die letztere Distanz variiren konnte, waren 69 und 70
Centimeter. Für diese beiden Werthe die Intensität x der
Lampe und den Werth D berechnet, findet man
x
=
4,43
D
=
27c,09
=
4,37
=
27,26.
Nachdem die Lampe eine Stunde gebrannt, war das Resultat der Messung ein anderes. Man
fand:
e = 60,5 η = 73,5,
woraus x = 4,9 und D =
27,21.
Der Werth von D ist nicht bedeutend geändert, was
anzeigt, daß die Versuche etwa gleich genau waren. Es hat sich also die Intensität
der verglichenen Lichter während der Stunde, die zwischen zwei Messungen verflossen,
geändert, und mag diese Aenderung hauptsächlich die Kerze getroffen haben.
III. Vergleichung der Intensität einer
Gasflamme mit jener der Normalkerze
A.
Die Gasflamme ist eine breite, sogenannte Schmetterlingsflamme. In den drei ersten
Versuchen war die breite, im vierten Versuche die schmale Seite der Flamme dem Apparate zugekehrt. Die
Versuche 2 und 3 wurden von anderen, ganz ungeübten Beobachtern angestellt:
beobachtet
berechnet
Versuch
1 : e = 102 η =
131,0
x = 14,846 D = 26,47
„
2 : e = 101 η = 129,5
x = 14,533 D = 26,49
„
3 : e = 102 η = 130,0
x = 14,732 D = 26,338
„
4 : e =
98 η =
125,0
x = 13,611 D = 26,56
Die drei ersten, unter denselben Umständen, obgleich von verschiedenen Beobachtern
ausgeführten Messungen zeigen in ihren Angaben keine größere Differenz als 0,3
Lichtstärken oder etwa 2 Proc. der zu messenden Größe, – für photometrische
Messungen ein sehr günstiges Verhältniß. Daß im vierten Versuche eine kleinere
Intensität gefunden wurde, hat wohl nichts Befremdendes. Auffallend ist hingegen,
daß die Werthe von D zwar unter einander gut stimmen,
allein nicht ganz unbedeutend von dem D, das aus den Vergleichungen von
Kerze mit Kerze und Kerze mit Lampe sich ergab, abweichen. Zum Theile mag sich diese
Abweichung aus dem Umstande erklären, daß die Gasflamme einen viel größeren Umfang
hat, als die anderen Flammen (für den vierten Versuch, in welchem die schmale Seite
der Flamme dem Apparat zugewendet war, ergibt sich ein etwas höherer Werth von D), zum größeren Theile dürfte die Ursache jedoch in der
Verschiedenheit der Farben der Wachskerzen- und Gasflamme zu suchen seyn.
Erstere ist relativ gelbroth, letztere blau. – Die Verschiedenheit in der
Farbe des Lichtes erschwert alle photometrischen Messungen, – bei dem
besprochenen Apparate ist bei Anwendung ungleich gefärbter Flammen nie ein
gänzliches Verschwinden des Flecks zu erzielen, sondern nur ein Minimum seiner
Sichtbarkeit, welches aber mit großer Sicherheit die Stellung angibt, welche der
Apparat einnehmen muß. – Bei dem älteren Schattenphotometer bleibt die
Differenz in der Farbe der zu vergleichenden Lichter ungeschwächt, eben so bei Ritchie's Lichtmesser, – diese Photometer sind die
ungenauesten; – bei dem einfachen Bunsen'schen
Photometer ohne Spiegel findet schon eine Mischung der Farben statt, indem ja jede
Stelle des Schirmes im durchgelassenen und reflectirten Lichte zu gleicher Zeit
gesehen wird. Endlich bei dem Photometer mit Spiegeln ist die Vermischung eine viel
vollständigere, vermöge der häufigen Reflexionen des Lichtes und seines häufigen
Durchdringens des Papierschirmes. Auch in dieser Hinsicht dürfte das neue Instrument
vor früheren den Vorzug verdienen.
Die mitgetheilten Versuche sind ohne Benutzung des auf Lichtstärken getheilten Bandes
gemacht; sie erforderten zur Ermittelung des Resultates daher eine kleine Rechnung.
An dem Werth der gleichfalls berechneten Größe D, die
von früheren Versuchen bekannt, ließ sich der Grad der Genauigkeit der Messung
abnehmen.
Findet das Photometer Anwendung zur Beaufsichtigung öffentlicher Beleuchtungen, so
kann jede Rechnung erspart werden; man kann die Messung rasch, sicher und bequem
ausführen und besitzt in der Uebereinstimmung der Angaben der schwarzen und der
rothen Theilung eine Anzeige, ob der Versuch genau ausgeführt sey. Es war gerade
dieß das Anliegen, mit welchem der Magistrat der Stadt München sich an das
physikalische Institut wendete, und es wurde dem Verfasser durch den Vorstand des
Institutes, Hrn. Prof. Jolly, die Lösung der Aufgabe
anvertraut.
Tafeln