| Titel: | Ueber die Galvanometerwaage von Bourbouze; Bericht von Lissajous. |
| Fundstelle: | Band 207, Jahrgang 1873, Nr. LIX., S. 196 |
| Download: | XML |
LIX.
Ueber die Galvanometerwaage von Bourbouze; Bericht von Lissajous.
Aus dem Bulletin de la
Société d'Encouragement, December 1872, S. 673.
Mit Abbildungen auf Tab.
IV.
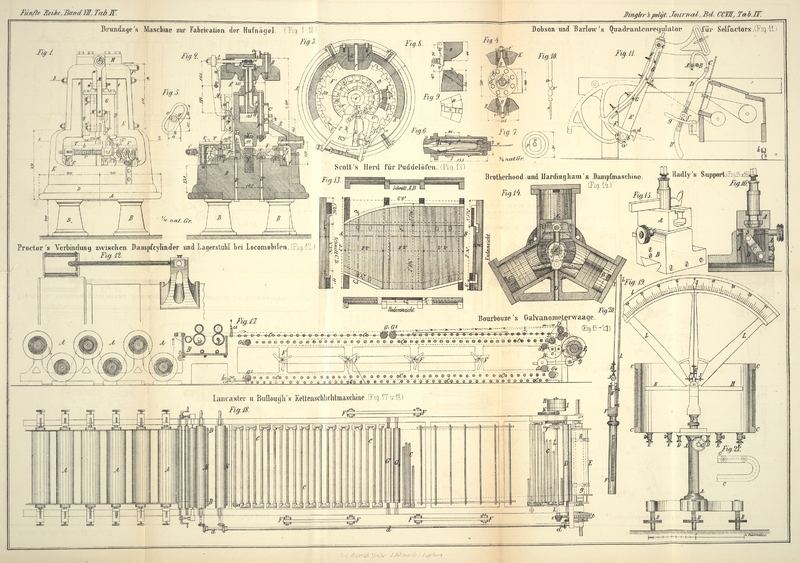
Bourbouze's Galvanometerwaage.
Dieses neue Instrument ist ein Galvanometer, dessen Multiplicatorrahmen mit
horizontalen Drahtwindungen umwickelt und dessen Nadel durch einen magnetisirten
Waagebalken ersetzt ist. Kleine mit Muttergewinden versehene Gewichte, welche sich
längs Schraubenspindeln vor- und zurückschrauben lassen, gestatten den
Schwerpunkt des Waagebalkens seitwärts oder aufwärts zu verrücken und dadurch
1) den Waagebalken horizontal zu stellen, indem man der Inclination, als Folge der
richtenden Wirkung des Erdmagnetismus, durch geeignete Entfernung jener Gewichte von
der Aufhängungsachse entgegenwirkt;
2) die Empfindlichkeit des Apparates zu reguliren, indem man die Hauptresultirende
der auf das System wirkenden Kräfte, wovon der von der Schwere herrührende Theil dem
Experimentator zur Verfügung steht, so nahe wie möglich an die Aufhängungsachse
bringt.
Ein langer und leichter Zeiger gibt auf einer Kreistheilung die Richtung und
Amplitude der Ablenkung an, welche der Magnetstab erfährt, sobald ein Strom im
Multiplicator circulirt. Das Instrument muß so orientirt werden, daß der Südpol des
Magnetstabes so nahe wie möglich nach Norden zeigt; sonst würde der Stab, bevor der
Strom den Apparat durchläuft, nur eine labile Gleichgewichtslage annehmen. Durch
Verschiebung der genannten Gewichtchen gelingt es rasch, den Magnetstab in der
erfahrungsmäßig richtigen Ebene horizontal zu stellen. Eben so kann man ihn durch
Verschiebung der Gewichte mehr oder weniger dem Zustande des indifferenten
Gleichgewichtes nähern, welcher ihm den Charakter einer astatischen Nadel verleihen
würde. Es läßt sich
demnach die Empfindlichkeit der Vorrichtung, je nach der Art des anzustellenden
Versuches, mehr oder weniger erhöhen. Ebenso kann die Empfindlichkeit des Apparates
dadurch modificirt werden, daß man den Magnetstab mehr oder weniger von der Mitte
des Multiplicators entfernt. Zu diesem Zweck läßt sich die Säule, welche den
magnetischen Waagebalken mit seinem Zeiger und den graduirten Bogen trägt,
vermittelst einer Zahnstange und eines Getriebes höher oder niedriger stellen. Die
speciellen Eigenschaften dieses Instrumentes sind durch den Gebrauch, welchen Hr.
Desains in seinen Vorlesungen während eines ganzen
Jahres fortwährend von demselben gemacht hat, außer Zweifel gesetzt, indem dasselbe
bei Vorführung der Inductionsphänomene und der elektrochemischen Wirkungen, sowie
bei den so difficilen Untersuchungen über strahlende Wärme ausgezeichnete Dienste
leistete. Wir können daher bestätigen, daß Hr. Bourbouze
die Wissenschaft mit einem sinnreichen Instrumente bereichert hat, welches mit
vollkommener Empfindlichkeit eine unbestreitbare Genauigkeit vereinigt.
Fig. 19
stellt das Instrument in der vorderen Ansicht, mit verticalem Durchschnitte der
Spule längs ihrer großen Achse dar. Fig. 20 ist eine
partielle Ansicht desselben im Profil und ohne Spule; Fig. 21 der Grundriß
eines Theiles der Spule.
A bezeichnet eine hohle Säule, welche den ganzen Apparat
trägt und auf einem Dreifuß befestigt ist. Letzterer läßt sich mittelst dreier
Fußschrauben B horizontal stellen. An die Säule A ist die flache zweidrähtige Spule C mit Hülfe einer Platte und vier Schrauben D befestigt. E sind
Klemmschrauben zur Verbindung der Leitungsdrähte mit der Spule. Die Säule F, welche den Waagebalken und den graduirten Quadranten
trägt, ist in der hohlen Säule verschiebbar und zu dem Ende mit einer Zahnstange
(Fig. 20)
versehen, in die ein kleines an die Säule A befestigtes
und durch einen Einschnitt der letzteren in das Innere hineinragendes Getriebe
greift. Zur Drehung dieses Getriebes dient ein an jedem Ende seiner Achse zu beiden
Seiten des Apparates befestigter Knopf G. Der Magnetstab
H oscillirt, wie der Balken einer Waage, in einer
auf dem Kopf der Säule F befestigten Gabel, und liegt
mittelst Schneiden auf stählernen Platten. Senkrecht auf der Mitte des Magnetes ist
ein langer Zeiger I befestigt, welcher über einem an die
Säule F befestigten Quadranten L spielt, um die durch elektrische Ströme hervorgerufene Ablenkung des
Magnetstabes anzuzeigen. Die Graduirung ist auf Glas ausgeführt, hinter welchem eine
Lichtquelle angeordnet wird, damit das Auditorium in einem Amphitheater den Vorgang
aus der Entfernung beobachten könne. Zur Regulirung der Horizontalität des
Waagebalkens H dienen die kleinen Massen J, J, welche sich durch Vor- und Zurückschrauben
auf der kleinen horizontalen Spindel dem Zeiger beliebig nähern oder von demselben
entfernen lassen. K sind ähnliche kleine Massen, die man
auf- und niederschraubt, je nachdem man den Schwerpunkt des Waagebalkens
höher oder tiefer legen will.
Um von dem Instrumente Gebrauch zu machen, versichert man sich zunächst vermittelst
der Fußschrauben B der Verticalität der Säule A, hebt dann durch Drehung des Knopfes G den Waagebalken bis über die Mitte der Spule, und
führt, indem man die Lage seines Schwerpunktes regulirt, die Zeigerspitzen auf den
Nullpunkt des Quadranten. Hierauf läßt man den galvanischen Strom durch den einen
oder den anderen der beiden Spulendrähte circuliren, oder auch, um die Intensität
der Wirkung zu erhöhen, durch beide zugleich. Der Zeiger nimmt alsdann eine sehr
langsame Bewegung an, und zeigt selbst unter dem Einfluß sehr schwacher Ströme eine
bedeutende Ablenkung.
Theorie der
Galvanometerwaage.
Nehmen wir der Einfachheit wegen an, die Drehungsachse des Magnetstabes sey
perpendiculär zur Pollinie und horizontal; letztere selbst sey horizontal, wenn die
Zeigernadel auf dem Nullpunkt der Theilung steht.
Fig. 1., Bd. 207, S. 197
Es sey AB (Fig.
1) die Pollinie des Magnetstabes, O die
Projection der Aufhängungsachse auf der durch AB gelegten Verticalebene; α der
azimuthale Winkel welchen diese Ebene mit dem magnetischen Meridian bildet; G der Schwerpunkt des Magnetstabes. In G wirkt das Gewicht p
des letzteren; A und B
sind die Angriffspunkte der Kräfte F und – F, welche das terrestrische Paar
bilden.
Zerlegen wir jede dieser Kräfte in drei Componenten: eine verticale, eine horizontale
perpendiculär zu AB, und in eine horizontale mit
AB in einer Ebene
liegende. Von diesen drei Componenten sind es nur die erste und dritte, welche auf
das Gleichgewicht des Magnetstabes AB influiren.
Bezeichnen wir die wirksamen horizontalen Componenten durch φ und – φ und die
verticalen Componenten durch f und – f, so ist offenbar
f = F sin I,
φ = F. cos I. cos
α
wobei I den Neigungswinkel
bezeichnet. Die drei Kräfe f, – f und p haben eine
Resultirende gleich ihrer Summe p, welche in einem
Punkte G¹ angreift, der eben so wie G auf einer zu AB
parallelen Linie liegt. Die Resultirende der beiden Kräfte p und – f greift in K an (wenn man p > f annimmt. Man hat daher
KG/KB =
f/p;
die Resultirende der in K wirkenden Kraft p – f und der Kraft f, welche in A angreift, ist in G¹ wirksam und es ergibt sich
KG¹/AG¹ = f/(p
– f), mithin
KG¹/KA = f/p = KG/KB;
die Punkte G¹ und G
liegen daher in gleichem Abstande von AB. Ferner
ist der Punkt G¹ in Bezug auf den Magnetstab
fest, welches auch die Neigung des letzteren seyn möge. Die drei
Regulirungsgewichtchen setzen uns in den Stand, den Schwerpunkt des Systemes zu
verrücken; mit Hülfe der seitlichen Gewichte können wir ihn in die zum Waagebalken
Senkrechte verlegen, welche durch den Punkt O geht; das
dritte Gewicht dient zur Hebung oder Senkung es Schwerpunktes. Will man sich des
Instrumentes bedienen, so beginnt man mit der Verschiebung der horizontalen Massen,
bis der Waagebalken horizontal steht. Damit diese Bedingung erfüllt sey, ist es
offenbar nothwendig, daß der Punkt G¹ in der zu
AB perpendiculären Linie OQ liege.
Wenn wir nun AB aus der horizontalen Lage
entfernen, so wirkt auf den Waagebalken ein System von Kräften, deren statisches
Moment mehr oder weniger groß ist. Dieses Totalmoment, auf den Punkt O bezogen, liefert offenbar das Empfindlichkeitsmaaß des
Galvanometers. Seine Berechnung ist es, worauf der ganze Nutzen der Theorie des in
Rede stehenden Instrumentes beruht. Um nun dieses Moment zu berechnen, bemerken wir,
daß die in's Spiel kommenden Kräfte sich reduciren auf
φ
wirkend
in
A,
– φ
„
„
B,
p
„
„
G¹.
Es sey OG¹ (Fig.
2) durch d, AB durch 2a, und der Winkel welchen die Linie
AB mit dem Horizont bildet, durch ω bezeichnet. Lassen wir in O zwei gleiche Kräfte p und
– p angreifen. Die Kraft p wird durch den Widerstand des Stützpunktes aufgehoben; es wirken alsdann auf das System,
zwei Kräftepaare (p – p), (φ – φ).
Fig. 2., Bd. 207, S. 199
Betrachtet man die Momente, welche AB auf dem kürzesten Wege in die horizontale
Lage zurückzubringen streben, als positiv d.h. in der Richtung des Pfeiles
wirkend, so ist das totale Moment
M = 2φa . sin ω + pd . sin
ω
Setzt man nun
M = μ .
sin ω
so ergibt sich
μ = 2 φa + pd = 2 aF .
cos I . cos α. + pd
Die Discussion dieser Formel wird die merkwürdigen Eigenschaften der
Galvanometerwaage näher hervortreten lassen. Wir sehen schon aus der einfachen
Betrachtung der Formel M = μ . sin ω, daß der unter irgend einem Azimuth horizontal
in's Gleichgewicht gesetzte Waagebalken unter jedem Azimuth ohne Ausnahme das
Gleichgewicht im horizontalen Sinne behauptet. Die durch μ dargestellte Empfindlichkeit ändert sich mit dem Azimuth, weil
μ eine Function von α ist. Man kann d so wählen, daß unter
einem beliebigen Azimuth μ > 0, = 0 oder <
0 wird.
Für μ > 0 ist das Gleichgewicht stabil,
für μ < 0 ist das Gleichgewicht labil.
Ist endlich μ = 0, so ist das Gleichgewicht indifferent und die Nadel wird in strengem Sinne
astatisch. Man kann demnach dem Galvanometer jeden beliebigen Grad der
Empfindlichkeit ertheilen. Gibt man im Voraus dem d
einen bestimmten Werth, so läßt sich leicht nachweisen, wie sich die Zeigernadel bei
den verschiedenen Azimuthen verhalten wird. Ist nämlich pd > 0 und > 2aF . cos I, so ist
μ immer > 0 und das Gleichgewicht immer
stabil; ist pd < 0 und sein absoluter Werth
größer als 2aF . cos I, so ist das Gleichgewicht immer
labil. Es ist stabil für gewisse Werthe von d und labil
für andere Werthe, wenn pd innerhalb + 2aF . cos I. und – 2aF .
cos I liegt. In diesem Falle ist in der That μ immer Null für einen gewissen Werth von α; denn, löst man die Gleichung μ = 0 nach cos α auf, so ergibt
sich
cos α = – pd/(2aF . cos I)
ein Werth, der zwischen – 1 und + 1 liegt. Bezeichnet
A den aus dieser Gleichung gezogenen Werth von α, so ist für α =
A, μ = 0 und das Gleichgewicht ist indifferent. Ist der absolute Werth von α kleiner als A, so
ist das Gleichgewicht stabil, ist er größer als A, so
ist das Gleichgewicht labil.
Fig. 3., Bd. 207, S. 200
Vorstehende Discussion läßt sich in Form einer ganz einfachen geometrischen
Construction übersichtlich darstellen. Es sey C¹OC (Fig.
3) eine Horizontale. Zieht man eine Linie OA = 2aF, welche mit OC einen Winkel COA =
I bildet, und projicirt dieselbe auf OC, so ist
OC = 2a F
. cos I.
Man beschreibe nun über CC¹ als Durchmesser den
Kreis C¹HC, zähle die
Bögen von C als Anfangspunkt aus, trage von O aus eine Länge OP = pd in der Richtung OC¹ ab, wenn d < 0, und in der
umgekehrten Richtung, wenn d < 0, und errichte in
P ein Perpendikel KK¹. Für alle Azimuthe von OC bis OK und OK¹ wird das
Gleichgewicht des Stabes stabil, für alle Azimuthe von OC¹ bis OK und OK¹ wird es labil seyn. Liegt der Punkt P jenseits C¹, so ist das Gleichgewicht
für alle Azimuthe stabil; entfernt sich jedoch P in der
Richtung OC über den Punkt C
hinaus, so ist es labil.
Zur Erhöhung der Empfindlichkeit seines Instrumentes hat Bourbouze die Massen so angeordnet, daß man die drei
Gleichgewichtszustände, den stabilen, labilen und den indifferenten erhalten kann,
wenn der Südpol des Magnetstabes genau nach Norden gerichtet ist, d.h. wenn α = 0. Hieraus folgt, daß pd < 0 ist und von 0 bis – 2aF .
cos (1 – ε) variiren kann, wobei
ε eine sehr kleine Größe bezeichnet. Stellt
man das Gleichgewicht unter einem Azimuth α
< 90° her, so muß der absolute Werth von pd ein wenig kleiner als 2aF . cos I cos
α seyn. Wendet man den Magnet vollständig bis zu seiner
entgegengesetzten Lage, was mit dem Zeichenwechsel von cos
α gleichbedeutend ist, so ist das Moment 2a F
. cos I cos α + pd aus zwei negativen
Ausdrücken zusammengesetzt, daher negativ und das Gleichgewicht labil. Diese
merkwürdige Eigenschaft steht, wie aus vorstehender Discussion hervorgeht, mit der
von Bourbouze adoptirten eigenthümlichen Vertheilung der
Massen in wesentlichem Zusammenhange, und ist eine Garantie für die Empfindlichkeit
des Apparates.
Tafeln